Please refer to Matrices Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Mathematics Important Questions Matrices
Very Short Answer Questions
Question.

Answer.
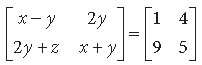
On comparing the corresponding elements, we get
x – y = 1, 2y = 4, 2y + z = 9, x + y = 5
⇒ y = 2, x = 3, z = 5
∴ x + y + z = 3 + 2 + 5 = 10.
Question.
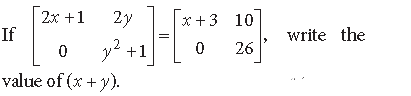
Answer.
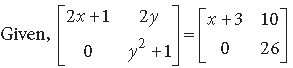
⇒ 2x + 1 = x + 3, 2y = 10, y2 + 1 = 26
⇒ From first two equations, we get x = 2, y = 5
which also satisfies y2 + 1 = 26
∴ x + y = 2 + 5 = 7
Question.
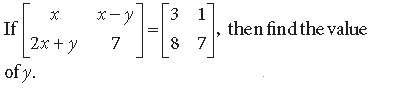
Answer.
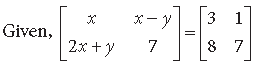
⇒ x = 3, x – y = 1, 2x + y = 8
⇒ x = 3, y = 2.
Also, 2x + y = 8 is satisfies by x = 3 and y = 2
∴ x = 3 and y = 2.
Question.
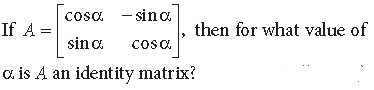
Answer.

By equality of two matrices, corresponding elements are equal.
∴ cos α = 1 ⇒ α = 0 and sin α = 0 ⇒ α = 0
∴ α = 0
Question.
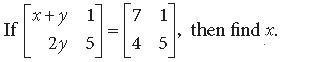
Answer.
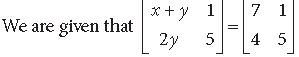
By equality of two matrices, we get
2y = 4 ⇒ y =2
Also, x + y = 7 ⇒ x + 2 = 7 ⇒ x = 5.
Question.

Answer.

By equality of two matrices, we have
3y – x = 5 and –2x = –2 ⇒ x = 1
Putting the value of x, we get
3y – 1 = 5 ⇒ 3y = 6 ⇒ y = 2
Question. Find the values of x and y, if
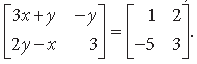
Answer.

Question. Find the values of x and y, if
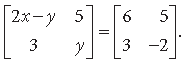
Answer. We are given that

Question.

Answer. By equality of two matrices, we get
x + y = 8, x – y = 2 and y = 3
Now, y = 3
∴ x + y = 8 ⇒ x + 3 = 8 ⇒ x = 5
Also x – y = 2 is satisfied by x = 5 and y = 3
∴ x = 5
Question.
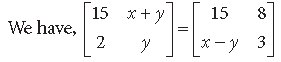
Answer.
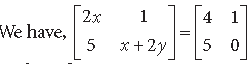
By equality of two matrices, we get
2x = 4 ⇒ x = 2 and x + 2y = 0
Now, x + 2y = 0 ⇒ 2 + 2y = 0
⇒ 2y = – 2 ⇒ y = – 1
∴ x = 2 and y = – 1
Question.

Answer.

Question.

Answer.
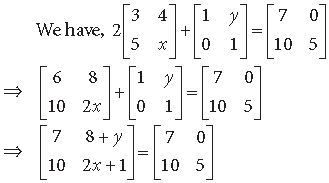
On comparing corresponding elements of the matrices, we get
8 + y = 0 and 2x + 1 = 5 ⇒ y = –8 and x = 2
∴ x – y = 2 + 8 =10
Question.
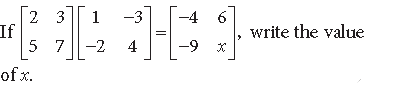
Answer.
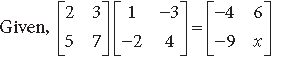
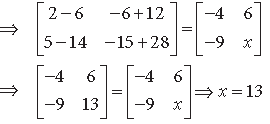
Question. Find the value of x + y from the following
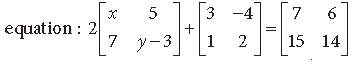
Answer.

⇒ 2x + 3 = 7, 2y – 4 = 14
⇒ 2x = 4, 2y = 18 ⇒ x = 2, y = 9
∴ x + y = 2 + 9 = 11
Question.
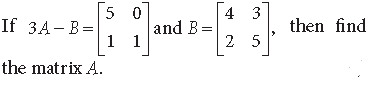
Answer.

Question.

Answer.
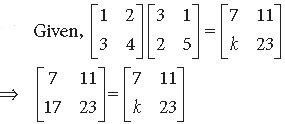
On comparing the corresponding elements of matrices, we get k = 17
Question.
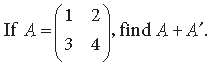
Answer.
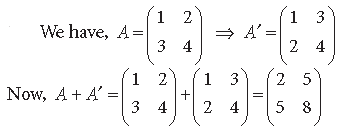
Question.

Answer.
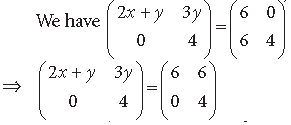
By equality of two matrices, we have
2x + y = 6 and 3y = 6 ⇒ y = 2.
Putting the value of y, we get
2x + 2 = 6 ⇒ 2x = 4 ⇒ x = 2.
Question. If matrix A = [1 2 3], then find AA’ where A’ is the transpose of matrix A.
Answer.
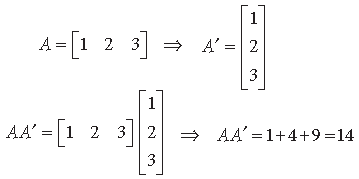
Question.
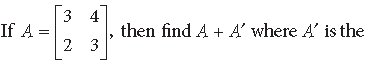
Answer.
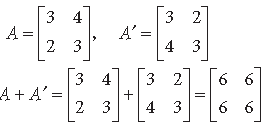
Question.
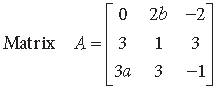
is given to be symmetric, find values of a and b.
Answer.

Question.
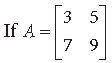
is written as A = P + Q, where P is a symmetric matrix and Q is a skew symmetric matrix, then write the matrix P.
Answer.
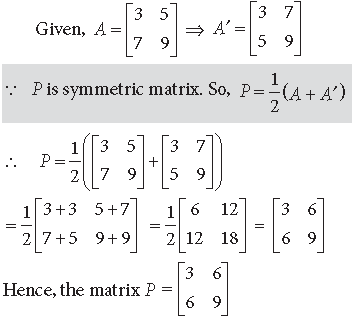
Question. Express the matrix
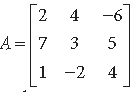
as the sum of a symmetric and a skew symmetric matrix.
Answer. We know that a square matrix A can be written as

Question. Write a 2 × 2 matrix which is both symmetric and skew symmetric.
Answer.

Question. Use elementary column operations C2 → C2 – 2C1 in the matrix equation
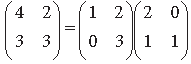
Answer.
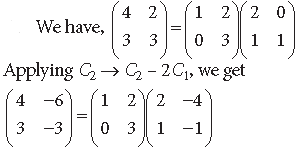
Question. Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3.
Answer. As matrix is of order 2 × 2, so there are 4 entries possible.
Each entry has 3 choices i.e. 1, 2 or 3. So, the number
of ways to make such matrices is 3 × 3 × 3 × 3 = 81.
Question. Write the element a23 of a 3 × 3 matrix A = [aij] whose elements aij are given by

Answer.

Question. The elements aij of a 3 x 3 matrix are given by
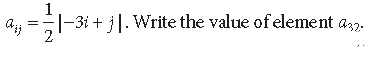
Answer.
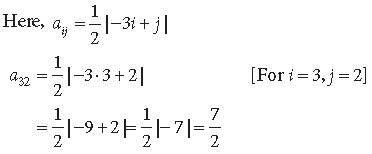
Question. For a 2 x 2 matrix A = [aij], whose elements are given by

Answer.

Question. For a 2 x 2 matrix, A = (aij) whose elements are given by aij = i/j write the value of a12
Answer.

Question. If a matrix has 5 elements, then write all possible orders it can have.
Answer. The possible orders are 1 x 5 or 5 x 1.
Question.
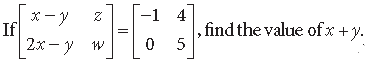
Answer.
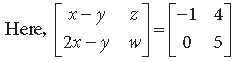
⇒ x – y = – 1, z = 4, 2x – y = 0, w = 5
Solving these equations for x and y, we get
x = 1, y = 2
∴ x + y = 1 + 2 = 3.
Question.
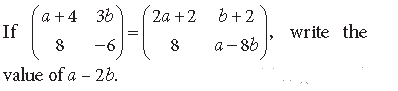
Answer.
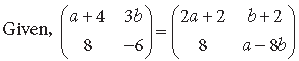
By equality of matrices, we get
a + 4 = 2a +2, 3b = b +2, – 6 = a – 8b
On solving these equations, we get a = 2, b = 1.
So a – 2b = 0.
Question.
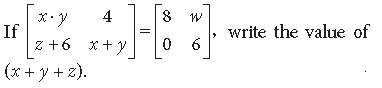
Answer.
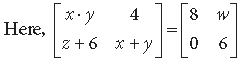
⇒ x · y = 8, w = 4
z + 6 = 0, x + y = 6
⇒ z = – 6, x + y = 6
⇒ x + y + z = 6 – 6 = 0.
Question. Find the value of a if
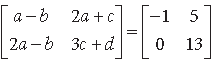
Answer.
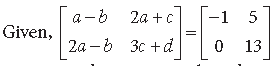
On comparing the corresponding elements, we get
a – b = – 1, 2a – b = 0
On subtraction, we get a = 1.
Question. ……… matrix is both symmetric and skew-symmetric matrix.
Answer. Null.
Question. Sum of two skew-symmetric matrices is always ……… matrix.
Answer. Let A is a given matrix, then (– A) is a skew-symmetric matrix.
Similarly, for a given matrix – B is a skew-symmetric matrix.
Hence, – A – B = – (A + B) ⇒ sum of two skew-symmetric matrices is always skew-symmetric matrix.
Question. Matrix multiplication is …… over addition.
Answer. Matrix multiplication is distributive over addition.
e.g., For three matrices A, B and C,
(i) A (B + C)= AB + AC
(ii) (A + B)C = AC + BC
Question. If A is a symmetric matrix, then A3 is a ……… matrix.
Answer. If A is a symmetric matrix, then A3 is a symmetric matrix.
∵ A’ = A
∴ (A3) ‘= A‘3
= A3 [ ∵ (A)n‘ = (An)’]
Question. The negative of a matrix is obtained by multiplying it by ……… .
Answer. Let A is a given matrix.
∴ – A = – 1[A]
So, the negative of a matrix is obtained by multiplying it by – 1.
Question. If A is a skew-symmetric, then kA is a ……… (where, k is any scalar).
Answer. If A is a skew-symmetric, then kA is a skew-symmetric matrix (where, k is any scalar).
[ ∵A’ = – A ⇒ (kA)’ = k(A)’= – (kA)]
Question. In applying one or more row operations while finding A-1 by elementary row operations, we obtain all zeroes in one or more, then A-1 ……… .
Answer. In applying one or more row operations while finding A-1 by elementary row operations, we obtain all zeroes in one or more, then A-1 does not exist.
Question. If A and B are symmetric matrices, then
(i) AB – BA is a ………
(ii) BA – 2AB is a ………
Answer. (i) AB – BA is a skew-symmetric matrix.
Since, [AB – BA]’ = (AB)’ – (BA)’
= B’A’ – A’B’ [ ∵(AB)’ = B’A’]
= BA – AB [ ∵A’ = A and B’ = B]
= – [AB – BA]
So, [AB – BA] is a skew-symmetric matrix.
(ii) [BA – 2 AB] is a neither symmetric nor skew-symmetric matrix.
∴ (BA – 2 AB)’ = (BA)’ – 2(AB)’
= A’B’ – 2B’A’
= AB – 2BA
= – (2BA – AB)
So, [BA – 2 AB] is neither symmetric nor skew-symmetric matrix.
Short Answer Type Questions
Question.
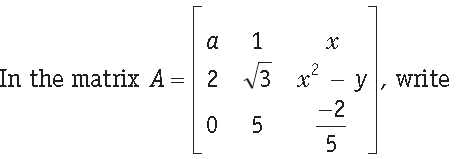
(i) the order of the matrix A.
(ii) the number of elements.
(iii) elements a23, a31 and a12.
Answer. We have

(i) the order of matrix A = 3 x 3
(ii) the number of elements = 3 x 3 = 9
[since, the number of elements in an m ´ n matrix will be equal to m x n = mn
(iii) a23 = x2 – y, a31 = 0, a12 = 1
Question. Construct a2 x 2 matrix, where

Answer.

Question. If possible, find the sum of the matrices A and B, where
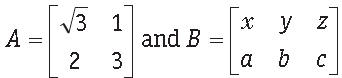
• Thinking Process
We know that, two matrices are added, if they have same order.
Answer. We have,
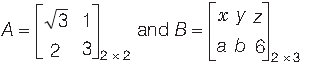
Here, A and B are of different orders. Also, we know that the addition of two matrices A and B is possible only if order of both the matrices A and B should be same. Hence, the sum of matrices A and B is not possible
Question.
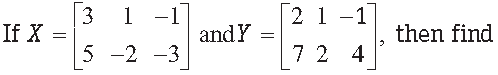
(i) X + Y.
(ii) 2X – 3Y.
(iii) a matrix Z such that X + Y + Z is a zero matrix.
Answer.
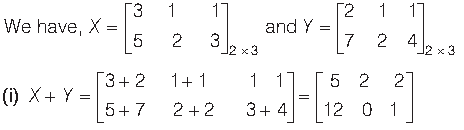
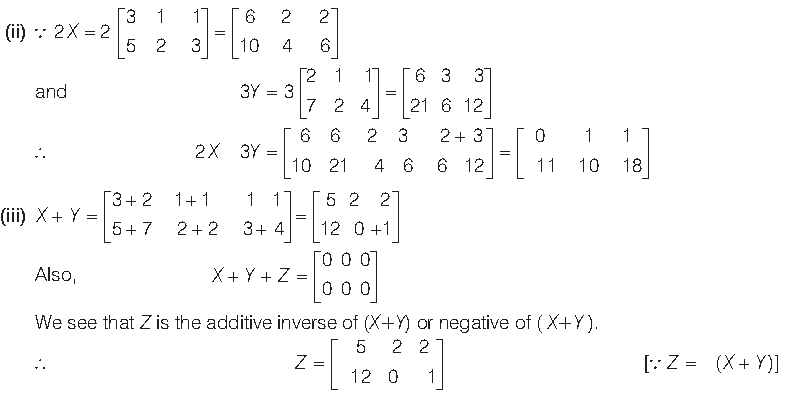
Question.
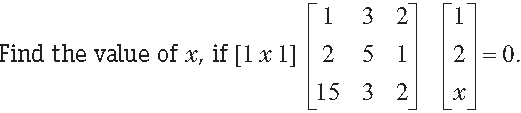
Answer.
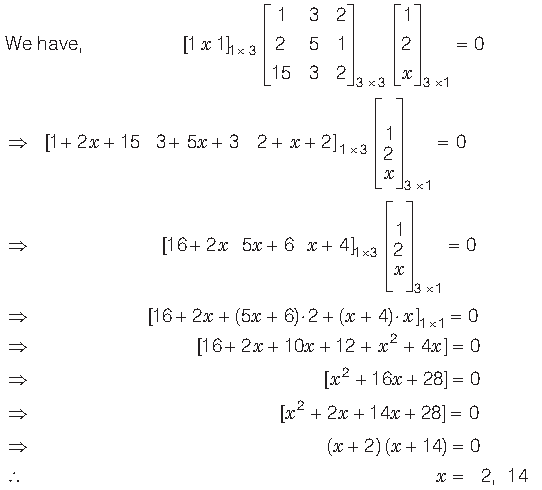
Question.
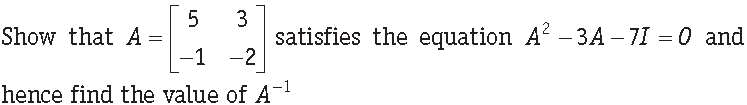
Answer.


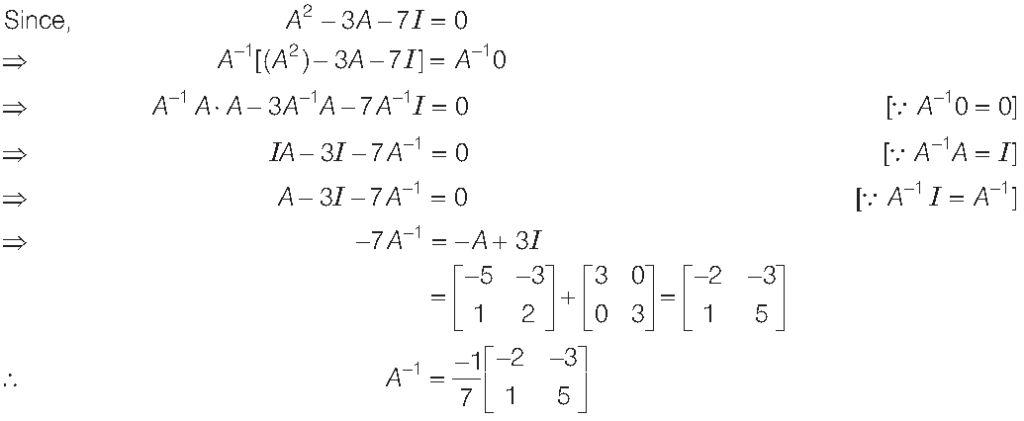
Question.
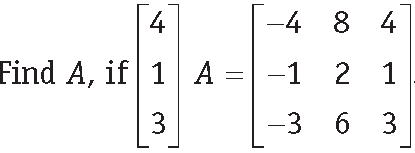
Answer.


Question.
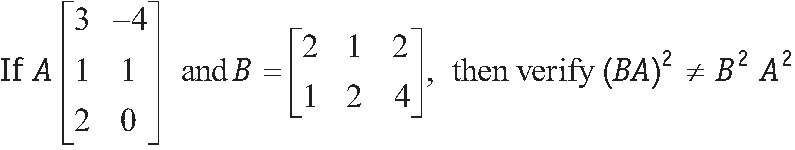
Answer.

Question. Using elementary row transformations, find the inverse of the following matrix.
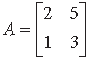
Answer.
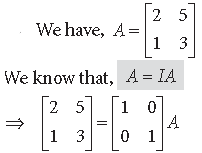

Question. In a parliament election, a political party hired a public relations firm to promote its candidates in three ways-telephone, house calls and letters. The cost per contact (in paise) is given in matrix A a

Find the total amount spent by the party in the two cities. What should one consider before casting his/her vote-party’s promotional activity or their social activities?
Answer. The total amount spent by the party in two cities X and Y is represented in the matrix equation by matrix C as,
C = BA

∴ X = ₹ 990000 and Y = ₹ 2120000
i.e., Amount spent by the party in city X and Y is ₹ 990000 and ₹ 2120000 respectively. One should consider about the social activity before casting his/her vote.
Question. A trust fund, ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Using matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200. What are the values reflected in this question?
Answer. Trust fund = ₹ 35,000.
Let ₹ x be invested in the first bond and then
₹ (35,000 – x) will be invested in the second bond.
Interest paid on the first bond = 8% = 0.08
Interest paid on the second bond = 10% = 0.10
Total annual interest = ₹ 3,200.
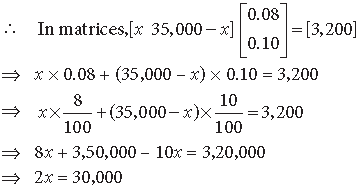
⇒ x = 15,000
∴ ₹ 15,000 should be invested in the first bond and
₹ 35,000 – ₹ 15,000 = ₹ 20,000 be invested in the second bond.
The values reflected in this question are :
(i) Spirit of investment.
(ii) Giving charity to cancer patients.
(iii) Helping the orphans living in the society.
Question.

Answer.

Question. Express the following matrix as the sum of a symmetric and skew symmetric matrix and verify your result.

Answer. We know that
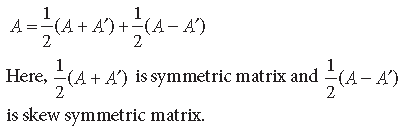

Long Answer Type Questions
Question. Using elementary row transformations, find the inverse of the following matrix :
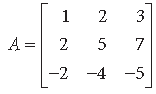
Answer.
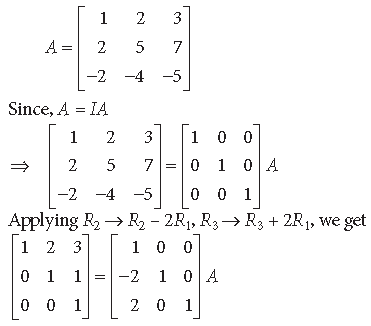
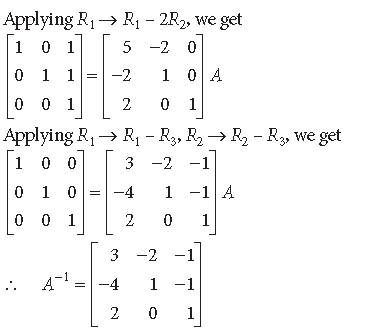
Question. Find the inverse of the following matrix using elementary operations :

Answer.


CASE STUDY:
Amit, Biraj and Chirag were given the task of creating a square matrux of order 2.
Below are the matrices created by them. A, B , C are the matrices created by Amit, Biraj and Chirag respectively.

If a = 4 and b = −2, based on the above information answer the following:
Question. Sum of the matrices A, B and C , A+(𝐵+𝐶) is

Answer
C
Question. (𝐴𝑇)𝑇 is equal to

Answer
A
Question. AC−𝐵𝐶 is equal to
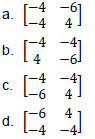
Answer
C
Question. (𝑎+𝑏)𝐵 is equal to
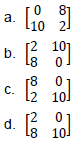
Answer
C
CASE STUDY:
On her birth day, Seema decided to donate some money to children of an orphanage home. If there were 8 children less, everyone would have got Rs.10 more. However, if there were 16 children more, everyone would have got Rs. 10 less. Let the number of children be x and the amount distributed by Seema for one child be y (in Rs.).
Based on the information given above, answer the following questions:
Question. The equations in terms x and y are
a. 5x-4y = 40
5x-8y = -80
b. 5x-4y = 40
5x-8y = 80
c. 5x-4y = 40
5x+8 y= -80
d. 5x+4y = 40
5x-8y = -80
Answer
A
Question. Which of the following matrix equations represent the information given above?

Answer
C
Question. The number of children who were given some money by Seema, is
a. 30
b. 40
c. 23
d. 32
Answer
D
Question. How much amount is given to each child by Seema?
a. Rs. 32
b. Rs. 30
c. Rs. 62
d. Rs. 26
Answer
B
Question. How much amount Seema spends in distributing the money to all the students of the Orphanage?
a. Rs. 609
b. Rs. 960
c. Rs. 906
d. Rs. 690
Answer
B

