Please refer to MCQ Questions Chapter 7 Integrals Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 7 Integrals in Class 12 Mathematics provided below to get more marks in exams.
Chapter 7 Integrals MCQ Questions
Question. Consider the following statements
Statement-I: The value of

Statement-II: The value of


(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
A
Question. ∫ cos {2tan-1√1-x/1+x dx is equal to
(a) 1/8(x2-1) + k
(b) 1/2 x2+k
(c) 1/2 x+k
(d) None of these
Answer
B
Question. Value of

(a) 2sin-1√x/a + c
(b) -2sin-1√x/a + c
(c) 2sin-1√x/a + c
(d) None of these
Answer
A
Question. ∫sec2/3 x cosec4/3 x dx =
(a) –3(tanx)1/3 + c
(b) –3(tanx)–1/3 + c
(c) 3(tanx)–1/3 + c
(d) (tan x) –1/3 + c
Answer
B
Question.
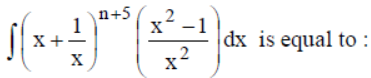
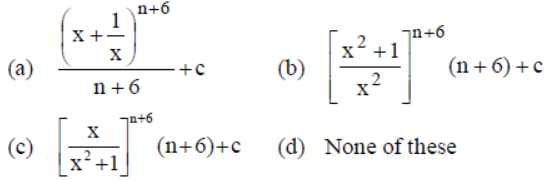
Answer
A
Question.
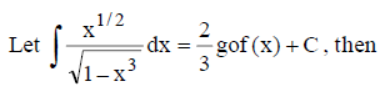
(a) cos 1/3
(b) sin 1/2
(c) 2 cos 2
(d) 0
Answer
D
Question. ∫ex (1-sinx/1-cosx) dx is equal to
(a) -ex tan(x/2)+ C
(b) -ex cot(x/2)+ C
(c) -1/2 ex tan(x/2)+ C
(d) 1/2 ex cot(x/2)+ C
Answer
B
Question. If θ1 and θ2 be respectively the smallest and the largest values of θ in (0,2π) – {π} which satisfy the equation, (image 74) is equal to:
(a) π/3
(b) 2π/3
(c) π/3 + 1/6
(d) π/9
Question. (image 28)
(where C is a constant of integration), then the ordered pair (A, B) is equal to
(a) (– 2, – 1)
(b) (2, – 1)
(c) (– 2, 1)
(d) (2, 1)
Question. If ƒ(3x – 4) / (3x + 4) = x + 2, x ≠ − 4/3, and ∫ƒ(x) dx = A log |1 – x | + Bx + C, then the ordered pair (A, B) is equal to :
(where C is a constant of integration)
(a) (8/3, 2/3)
(b) (− 8/3, 2/3)
(c) (− 8/3, − 2/3)
(d) (8/3, − 2/3)
Question. Let ƒ : R → R be a continuously differentiable function such that ƒ(2) = 6 and ƒ’(2) = 1/48. If (image 75) is equal to :
(a) 18
(b) 24
(c) 12
(d) 36
Question. (image 45)
(a) (1/√2)log | tan(x/2 + 3π/8) | + c
(b) (1/√2)log | cot(x/2) | + c
(c) (1/√2)log | tan(x/2 − 3π/8) | + c
(d) (1/√2)log | tan(x/2 − π/8) | + c
Question. If (image 46) then value of (A, B) is
(a) (-cos α,sin α)
(b) (cos α, sin α)
(c) (-sin α, cos α)
(d) (sin α,cos α)
Question. Let (image 5) Then ƒ(3) – ƒ(1) is equal to :
(a) − π/12 + 1/2 + √3/4
(b) π/6 + 1/2 − √3/4
(c) − π/6 + 1/2 + √3/4
(d) π/12 + 1/2 − √3/4
Question. If (image 8) where C is a constant of integration, then the ordered pair (λ, f(θ)) is equal to:
(a) (1, 1 – tanθ)
(b) (–1, 1 – tanθ)
(c) (–1, 1 + tanθ)
(d) (1, 1 + tanθ)
Question. Let α β (0, π/2) be fixed. If the integral
(image 11)
where C is a constant of integration, then the functions A(x) and B(x) are respectively :
(a) x + α and loge |sin(x + α)|
(b) x – α and loge |sin(x – α)|
(c) x – α and loge |cos(x – α)|
(d) x + α and loge |sin(x – α)|
Question. If ∫ cosn x sin x dx = -cos6 x/6 + C , then n =
(a) 0
(b) 1
(c) 2
(d) 5
Answer
D
Question. The value of integral ,

(a) 1/2
(b) 3/2
(c) 2
(d) 1
Answer
B
Question.
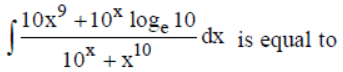
(a) 10x – x10 + C
(b) 10x + x10 + C
(c) (10x – x10)–1 + C
(d) loge(logx + x10) + C
Answer
D
Question.

(a) 1/5x(4+1/x2)-5 + C
(b) 1/5(4+1/x2)-5 + C
(c) 1/10x(1/x+4)-5 + C
(d) 1/10(1/x2+4)-5 + C
Answer
D
Question. Value of

(a) 2
(b) –2
(c) 1
(d) None of these
Answer
A
Question. Match the following definite integrals in column-I with their corresponding values in column-II.
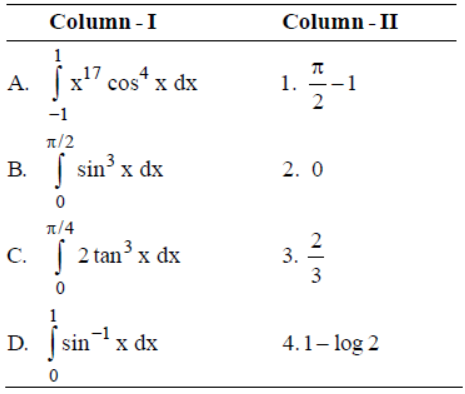
Codes
A B C D
(a) 1 3 2 4
(b) 2 3 4 1
(c) 1 2 3 4
(d) 2 4 3 1
Answer
B
Question. If for n ≥ 1, (image 115) then P10 – 90P8 is equal to:
(a) – 9
(b) 10e
(c) – 9 e
(d) 10
Question. Let F(x) = ƒ(x) + ƒ(1/x),where (image 134) Then F(e) equals
(a) 1
(b) 2
(c) 1/2
(d) 0
Question. (image 116)
(a) π/4 ln2
(b) π/8 ln2
(c) π/16 ln2
(d) π/32 ln2
Question. (image 160) is a polynomial of degree
(a) 5 in cot x
(b) 5 in tan x
(c) 3 in tan x
(d) 3 in cot x
Question. (image 161)
(a) (1/2) sec 1
(b) (1/2)cosec 1
(c) tan 1
(d) (1/2)tan 1
Question. The intercepts on x-axis made by tangents to the curve, (image 117) which are parallel to the line y = 2x, are equal to :
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 4
Question. Statement-1 : The value of the integral (image 118) is equal to π/6 Statement-2 : (image 118)
(a) Statement-1 is true; Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(b) Statement-1 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
(c) Statement-1 is true; Statement-2 is false.
(d) Statement-1 is false; Statement-2 is true.
Question. For 0 ≤ x ≤ π/2, the value of (image 119)
(a) π/4
(b) 0
(c) 1
(d) − π/4
Question. (image 120)
(a) π
(b) π/2
(c) 4π
(d) π/4
Question. (image 121)
(a) log 2√2
(b) log 2
(c) 2 log 2
(d) log √2
Question. (image 122)
(a) y
(b) √(1+y2)
(c) x/√(1+y2)
(d) y2
Question. (image 123) then g (x + π) equals
(a) g (x) / g (π)
(b) g (x) + g (π)
(c) g (x) – g (π)
(d) g (x) . g (π)
Ans : b, c
Question. If [x] is the greatest integer ≤ x, then the value of the integral (image 124)
(a) 0.486
(b) 0.243
(c) 1.8
(d) 0
Question. (image 126)
(a) G(π/4) – G(π/16)
(b) 2[G(π/4) – G(π/16)]
(c) π[G(1/2) – G(1/4)]
(d) G(1/√2) – G(1/2)
Question. If (image 142) then the value of I2/I1 is
(a) 1
(b) –3
(c) –1
(d) 2
Question. (image 143)
(a) 2π
(b) π
(c) π/4
(d) 0
Question. ∫xx (1+ log x)dx is equal to
(a) x x
(b) x2x
(c) xx log x
(d) 1/2 (1 + log x)2
Answer
A
Question. The value of

(a) a sin-1(x/a) + √x2-a2 + C
(b) a sin-1(x/a) +√a2-x2 + C
(c) a sin-1(a/x) +√x2-a2 + C
(d) None of these
Answer
B
Question. Match the following integrals in column-I with their corresponding solutions in column-II. 31
Codes
A B C D
(a) 1 2 3 4
(b) 3 1 4 2
(c) 3 4 1 2
(d) 2 1 4 3
Answer
B
Question. If f and g are defined as f (x) = f (a – x) and g (x) + g (a – x) = 4, then
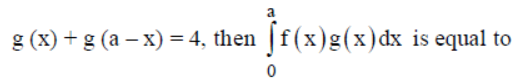
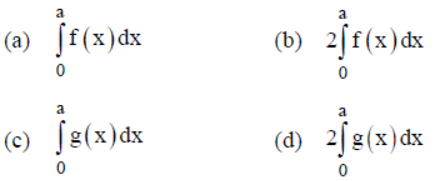
Answer
B
Question. If ∫ sin3 x cos5 x dx = A sin4 x + B sin6 x + C sin8 x + D.
Then
(a) A = 1/4 , B = -1/3 , C = 1/8 , D ∈ R
(b) A = 1/8 , B = 1/4 , C = 1/3 , D ∈ R
(c) A = 0 , B = -1/6 , C = 1/8 , D ∈ R
(d) None of these.
Answer
A
Question. Which of the following is/are correct?

(a) I and III are correct
(b) All are correct
(c) Only III is correct
(d) All are incorrect
Answer
C
Question. Value of
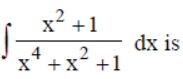
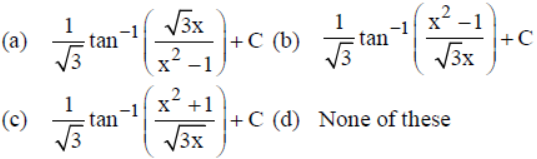
Answer
B
Question. ∫ tan-1 √x dx is equal to
(a) (x +1)tan-1 √x – √x + C
(b) x tan-1 √x – √x + C
(c) √x – x tan-1 √x + C
(d) √x – (x +1)tan-1 √x + C
Answer
A
Question. Consider the following statements
Statement-I : The value of
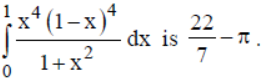
Statement-II : The value of integral

(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
C
Question.
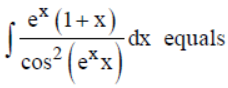
(a) – cot (exx) + C
(b) tan (xex) + C
(c) tan (ex) + C
(d) cot (ex) + C
Answer
B
Question. ∫x51(tan–1 x + cot–1x)dx
(a) x52/52(tan–1 x + cot–1 x) c
(b) x52/52 (tan–1 x – cot–1 x) c
(c) πx52/104 + π/2 + c
(d) x52/52 + π/2 + c
Answer
A
Question. Match the following derivatives of the functions in column-I with their respective anti-derivatives in column-II.
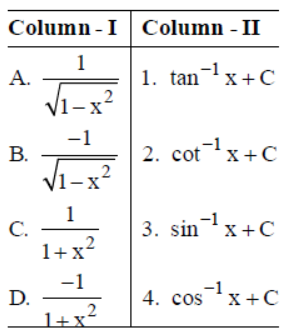
Codes
A B C D
(a) 1 2 3 4
(b) 3 4 2 1
(c) 3 4 1 2
(d) 4 3 2 1
Answer
C
Question. The integral ∫ sec2/3x xosex4/3 xdx xdx is equal to:
(Here C is a constant of integration)
(a) –3 tan–1/3 x + C
(b) – 3/4 tan–4/3 x + C
(c) –3 cot–1/3 x + C
(d) 3 tan–1/3 x + C
Question. If ∫ esecx (sec x tan f(x)+(sec x tan x + sec2x)) dx = esecx f(x) + C, then a possible choice of f(x) is:
(a) sec x + tan x + 1/2
(b) sec x – tan x – 1/2
(c) sec x + tan x – 1/2
(d) xsec x + tan x + 1/2
Question. If (image 58) is equal to:
(a) ln | x | – p (x) + c
(b) ln | x | + p (x) + c
(c) x – p (x) + c
(d) x + p (x) + c
Question. (image 59)
Ans : D
Question. Let f(x) be an indefinite integral of cos3x.
Statement 1: f(x) is a periodic function of period π.
Statement 2: cos3x is a periodic function.
(a) Statement 1 is true, Statement 2 is false.
(b) Both the Statements are true, but Statement 2 is not the correct explanation of Statement 1.
(c) Both the Statements are true, and Statement 2 is correct explanation of Statement 1.
(d) Statement 1 is false, Statement 2 is true.
Question. The value of (image 43)
(a) x + log | cos(x − π/4)| + c
(b) x − log | sin(x − π/4)| + c
(c) x + log | sin(x − π/4)| + c
(d) x − log | cos(x − π/4)| + c
Question. If (image 17)
where C is a constant of integration, then the function f(x) is equal to :
(a) 3/x2
(b) – 1/6x3
(c) – 1/2x2
(d) – 1/6x3
Question. Theintegral ∫ cos (loge x)dx is equal to :
(where C is a constant of integration)
(image 18)
Ans : C
Question. (image 89)
(a) 24/25
(b) 18/25
(c) 4/5
(d) 6/25
Question. The value of (image 90) where [t] denotes the greatest integer less than or equal to t, is:
(a) 1/12 (7π + 5)
(b) 1/12 (7π − 5)
(c) 3/20 (4π − 3)
(d) 3/10 (4π − 3)
Question. The integral (image 19) is equal to:
(where C is a constant of integration)
(image 19)
Ans : B
Question. The integral (image 107) is equal to :
(a) 1
(b) 6
(c) 2
(d) 4
Question. Let f : R → R be a function such that f(2 – x) = f(2 + x) and f(4 – x) = f(4 + x), for all x∈R and (image 108) Then the value of (image 108)
(a) 125
(b) 80
(c) 100
(d) 200
Question. If (image 20) for a suitable chosen integer m and a function A (x), where C is a constant of integration, then (A(x))m equals :
(a) −1/27x9
(b) −1/3x3
(c) 1/27x6
(d) 1/9x4
Question. If (image 21) where C is a constant of integration, then ƒ(x) is equal to:
(a) 1/3 (x + 1)
(b) 2/3 (x + 2)
(c) 2/3 (x − 1)
(d) 1/3 (x + 1)
Question. If ∫ x5e–4x3dx = (1/48)e–4x2 ƒ(x) + C, where C is a constant of integration, then ƒ(x) is equal to:
(a) – 2x3 – 1
(b) – 4x3 – 1
(c) – 2x3 + 1
(d) 4x3 + 1
Question. The integral (image 52) is equal to :
(where C is a constant of integration)
(image 52)
Ans : C
Question. If (image 24) and ƒ(0) = 0, then the value of ƒ(1) is:
(a) – 1/2
(b) – 1/4
(c) 1/2
(d) 1/4
Question. The integral (image 25) is equal to:
(where C is a constant of integration)
(image 25)
Ans : A
Question. (image 1)
(a) is equal to 1/2
(b) is equal to 1
(c) is equal to – 1/2
(d) does not exist
Ans : None
Question. If (image 2) where c is a constant of integeration, then g (0) is equal to:
(a) e
(b) e2
(c) 1
(d) 2
Question. If (image 26) (C is a constant of integration), then the ordered pair (K, A) is euqal to
(a) (2, 3)
(b) (2, 1)
(c) (– 2, 1)
(d) (– 2, 3)
Question. If (image 27) then ∫ ƒ(x) dx is equal to (where C is a constant of integration)
(a) 12 loge |1 – x| – 3x + c
(b) – 12 loge |1 – x| – 3x + c
(c) – 12 loge |1 – x| + 3x + c
(d) 12 loge |1 – x| + 3x + c
Question. If (image 31) where C is a constant, then g(b) is equal to :
(a) (1/√5)log(2 + √5)
(b) (1/2)log(2 + √5)
(c) 2 log(2 + √5)
(d) log(2 + √5)
Question. The integral (image 33) is equal to
(image 33)
Ans : D
Question. (image 95)
(a) ƒ”'(x) + ƒ'(x) = cos x – 2x sin x
(b) ƒ”'(x) + ƒ”(x) – ƒ'(x) = cos x
(c) ƒ”'(x) – ƒ”(x) = cos x – 2x sin x
(d) ƒ”'(x) + ƒ”(x) = sin x
Question. The value of integral (image 96)
(a) π/2(√2 + 1)
(b) π(√2 − 1)
(c) 2π(√2 − 1)
(d) π√2
Question. (image 79)
(a) (π – 2)/8
(b) (π – 1)/4
(c) (π – 2)/4
(d) (π – 1)/2
Question. The value of the integral (image 80)
(image 80)
Ans : 0
Question. The integral ∫ √(1+ 2cot x(cosec x + cot x))dx (0 < x < π/2) is equal to :
(where C is a constant of integration)
(image 30)
Ans : A
Question. The value of (image 77) where [t] denotes the greatest integer function, is:
(a) π
(b) –π
(c) –2π
(d) 2π
Question. The integral (image 34) is equal to:
(image 34)
Ans : B
Question. (image 16) is equal to :
(where c is a constant of integration.)
(a) 2x + sinx + 2 sin2x + c
(b) x + 2 sinx + 2 sin2x + c
(c) x + 2 sinx + sin2x + c
(d) 2x + sinx + sin2x + c
Question. The integral (image 35) is equal to:
(a) – x + (1 + x2) tan–1 x + c
(b) x – (1 + x2) cot–1 x + c
(c) – x + (1 + x2) cot–1x + c
(d) x – (1 + x2) tan–1 x + c
Question. If (image 12) where C is a constant of integration, then :
(a) A = 1/54 and f(x) = 3 (x – 1)
(b) A = 1/81 and f(x) = 3 (x – 1)
(c) A = 1/27 and f(x) = 9 (x – 1)
(d) A = 1/54 and f(x) = 9 (x – 1)2
Question. If f(x) is a non-zero polynomial of degree four, having local extreme points at x = –1, 0, 1; then the set S = {x ∈ R : f(x) = f(0)}contains exactly:
(a) four irrational numbers.
(b) four rational numbers.
(c) two irrational and two rational numbers.
(d) two irrational and one rational number.
Question. If the integral
(image 38)
where k is an arbitrary constant, then A is equal to :
(a) – 1/16
(b) 1/16
(c) 1/8
(d) – 1/8
Question. If the (image 39) then a is equal to :
(a) – 1
(b) – 2
(c) 1
(d) 2
Question. If (image 6) where C is a constant of integration, then the ordered pair (A(x), B(x)) can be :
(a) (x +1, – √x)
(b) (x +1, √x)
(c) (x -1, – √x)
(d) (x -1, √x)
Question. The integral (image 7) is equal to: (where C is a constant of integration)
(image 7)
Ans : A
Question. If (image 40) and ƒ(0) = 0, then ƒ(1) equals
(a) tan1 – π/4
(b) tan1 + 1
(c) π/4
(d) 1 – π/4
Question. Match the following integrals in column-I with their corresponding values in column-II.

Codes
A B C D
(a) 4 1 2 3
(b) 3 4 2 1
(c) 1 3 2 4
(d) 3 2 4 1
Answer
A
Question. Value of

(a) π/6
(b) π/12
(c) 12/π
(d) None of these
Answer
B
Question. If

(a) 3
(b) 4
(c) 6
(d) 8
Answer
A
Question. The integral
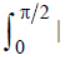
sin x cos x | dx is equal to :
(a) 2 √2
(b) 2( √2 -1)
(c) 2 -1
(d) None of these
Answer
B
We hope you liked the above provided MCQ Questions Chapter 7 Integrals Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.


