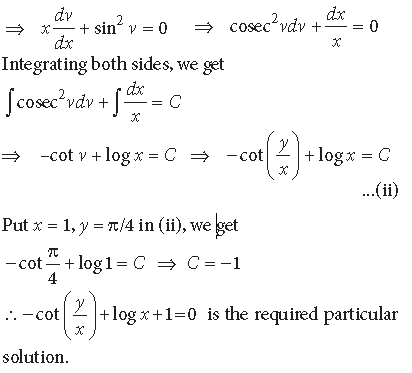Differential Equations Class 12 Mathematics Important Questions

Please refer to Differential Equations Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Mathematics Important Questions Differential Equations

Very Short Answer Type Questions

Question. Write the sum of the order and degree of the differential equation

Answer. Order = 2, Degree = 3
∴ Order + Degree = 2 + 3 = 5

Question. Write the degree of the differential equation.

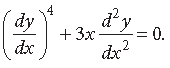
Answer. Degree of the given differential equation is 1.

Question. Write the degree of differential equation

Answer. Degree of the given differential equation is 2.

Question. Write the differential equation obtained by eliminating the arbitrary constant C in the equation representing the family of curves xy = C cos x. )
Answer. Here, xy = C cos x                 …(i)
Differentiating (i) w.r.t. x, we get

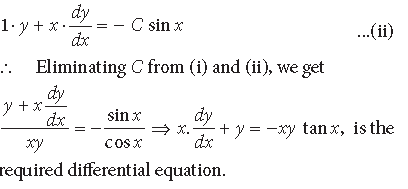
Question. Write the differential equation representing the family of curves y = mx, where m is an arbitrary constant. 
Answer. Here, y = mx                                         …(i)
Differentiating (i) w.r.t. x, we get

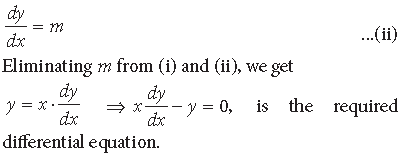
Question. Form the differential equation of the family of curves y = a cos (x + b), where a and b are arbitrary constants.
Answer. Here, y = a cos (x + b)                                     …(i)
Differentiating (i) w.r.t. x, we get

Question. Find the integrating factor of the differential equation

Answer.

Question. Write the degree of the differential equation

Answer. Degree of the given differential equation is 3.

Question. Write the degree of the differential equation :

Answer. The degree of the differential equation is 1.

Short Answer Type Questions

Question. Solve the following differential equation :

Answer.

Question. Solve the following differential equation :

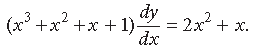
Answer.

Comparing coefficients of x, we get
1 = B + C                  …(ii)
Comparing constant terms, we get
0 = A + C ⇒ C = – A                …(iii)
Comparing coefficients of x2, we get 2 = A + B                … (iv)
Now solving (ii) & (iii), we get – A + B = 1                …(v)
Solving (iv) & (v), we get 2B = 3 ⇒ B = 3/2
Substituting the value of B in (2) & (5), we get
A =1/2 and C = –1/2

Question. Find the particular solution of the differential equation (1 – y²)(1 + logx)dx + 2xy dy = 0, given that y = 0 when x = 1.
Answer. We have, (1 – y²)(1 + log x) dx + 2xy dy = 0
∴ (1 – y²)(1 + log x) dx = – 2xy dy

Question. Solve the differential equation :

Answer.

Question. Solve the following differential equation y²dx + (x² – xy + y²)dy = 0 
Answer. We have, y² dx + (x² – xy + y²) dy = 0

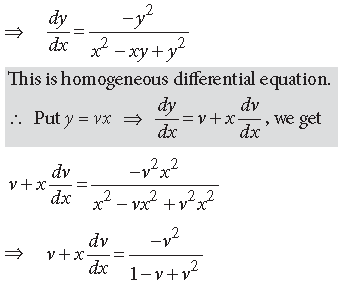
Question. Solve the following differential equation (cot^–1 y + x)dy = (1 + y²)dx
Answer. We have, (cot^–1y + x) dy = (1 + y²)dx

Question. Solve the following differential equation :
ex tan ydx + (1 – e^x)sec²ydy = 0. 
Answer. We have, ex tan ydx + (1 – e^x) sec² y dy = 0
⇒ e^x tan ydx = – (1 – ex) sec² y dy

Question. Solve the differential equation :
xdy + (y – x³)dx = 0. 
Answer. We have, xdy + (y – x³)dx = 0

Question. Solve the differential equation :
xdy – (y + 2x²)dx = 0.
Answer. We have, xdy – (y + 2x²)dx = 0

Question. Solve the following differential equation:

Answer.

Question. Solve the following differential equation :

Answer. We have,

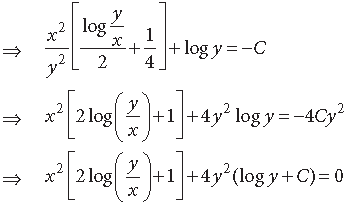
Question. Form the differential equation representing the family of ellipses having foci on x-axis and centre at the origin. 
Answer. The equation of family of ellipses is

Question. Form the differential equation representing the family of curves given by (x – a)² + 2y² = a², where a is an arbitrary constant. 
Answer. We have, (x – a)² + 2y² = a²
⇒ x² + 2y² – 2ax = 0 ⇒ x² + 2y² = 2ax                      …(i)
Differentiating (i) with respect to x, we get
2x + 4yy’ = 2a
Substituting the value of 2a in (i), we get
x² + 2y² = (2x + 4yy’)x
⇒ x² + 2y² = 2x² + 4xyy’
⇒ 2y² – x² = 4xyy’ ⇒ x² – 2y² + 4xyy’ = 0

Question. Form the differential equation of the family of curves y = A cos²x + B sin²x, where A and B are constants.
Answer. We have, y = Acos2x + Bsin2x                      …(i)
Differentiating (i) both sides w.r.t. x, we get
dy/dx = −2Asin2x + 2Bcos2x                                     …(ii)
Differentiating (ii) both sides w.r.t. x, we get

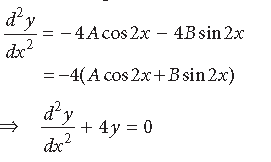
Question. Find the general solution of the following differential equation :

Answer.

Question. Find a particular solution of the differential equation dy/dx + 2y tan x = sin x, given that y = 0, when x = π/3.
Answer.

Question. Solve the following differential equation :
dy/dx + y = cos x − sin x. 
Answer.

Question. Find the particular solution of the differential equation log (dy/dx) = 3 + 4 , given that y = 0 when x = 0.
Answer.

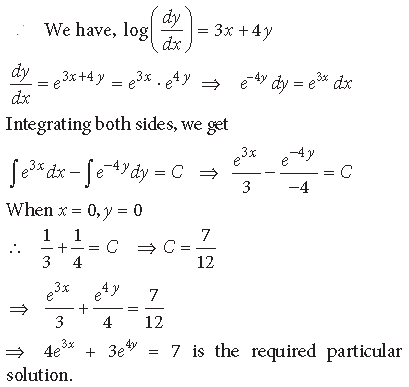
Question. Form the differential equation of the family of circles touching the x-axis at origin.
Answer. Equation of circle touching x-axis at origin is
x² + (y – a)² = a² ⇒ x² + y² – 2ay = 0                      …(i)
Differentiating (i) with respect to x we get

Question. Solve the differential equation (x² – yx²)dy + (y² + x²y²)dx = 0, given that y = 1 when x = 1.
Answer. We have, (x² – yx²)dy + (y² + x²y²)dx = 0
⇒ x²(1 – y)dy + y²(1 + x²)dx = 0

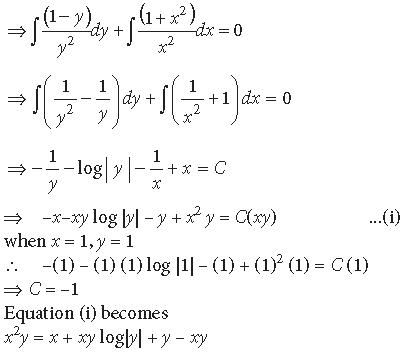
Question. Solve the differential equation dy/dx + y cot x = 2cos x, given that y = 0 when x = π/2.
Answer.

Question. Solve the following differential equation :

Answer.

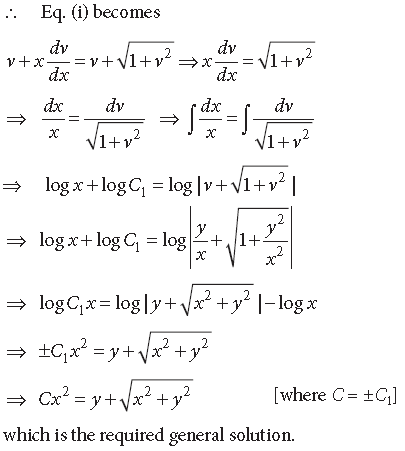
Question. Find the particular solution of the following

Answer.

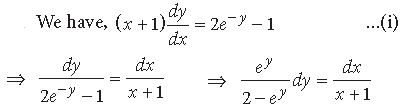
Integrating both sides, we get
–log (2 – e^y) = log (x + 1) + C                        …(ii)
(Taking 2 – e^y = t on L.H.S.)
when x = 0, y = 0
∴ – log (2 – 1) = log (0 + 1) + C   ⇒ C = 0
∴ Eq. (ii) becomes
– log (2 – e^y) = log (x + 1)
⇒ log (x + 1) log (2 – e^y) = 0
⇒ log (x + 1) (2 – e^y) = 0   ⇒ (x + 1) (2 – e^y) = 1
is the required particular solution.

Question. Find the particular solution of the following

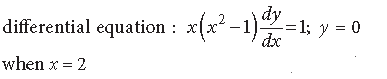
Answer.

Question. Solve the following differential equation :
(1 +x²) dy + 2xy dx = cot x dx; x ≠ 0
Answer. We have, (1 + x²) dy + 2xy dx = cot x dx; x ≠ 0

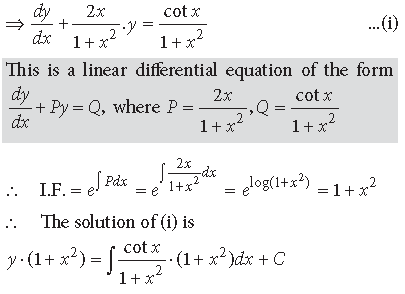
Question. Find the particular solution of the differential

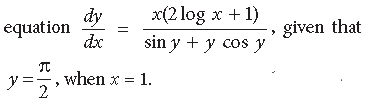
Answer.

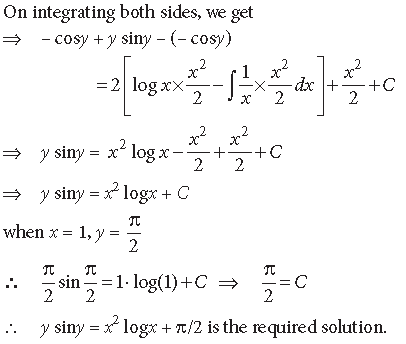
Question. Solve the following differential equation :
Answer.

Question. Find the particular solution of the differential
Answer.

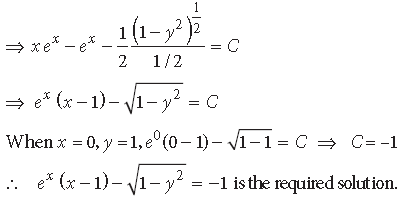
Question. Solve the following differential equation :
Answer.

Question. Find the particular solution of the differential equation dy/dx =1+ x + y + xy, given that y = 0 when x = 1
Answer.

Question. Find the particular solution of the differential equation x (1 + y²) dx – y (1 + x²)dy = 0, given that y = 1 when x = 0.
Answer. We have, x(1 + y²) dx – y(1 + x²) dy = 0

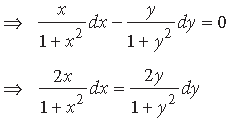
Integrating both sides, we get
log(1 + y²) = log(1+ x²) + log C
⇒ 1 + y² = C (1+ x²)
When x = 0, y = 1 ∴ 1 + 1 = C(1 + 0) ⇒ C = 2
∴ 1 + y² = 2(1 + x²) is the required particular solution.

Question. Find the particular solution of the differential equation : dy/dx + y cot x = 4x cosec x, (x ≠ 0), given that y = 0 when x = π/2
Answer.

Question. Solve the following differential equation :

Answer.

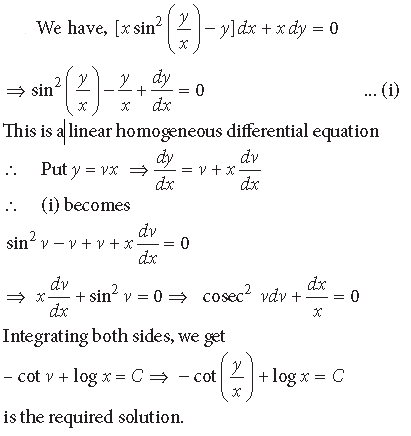
Question. Find the particular solution of the differential equation satisfying the given conditions :
dy/dx = y tan x, given that y = 1, when x = 0.
Answer.

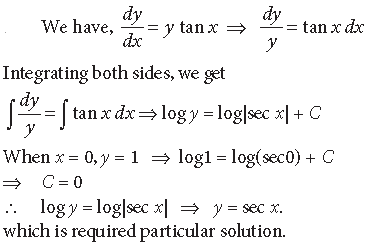
Question. Show that the following differential equation is homogeneous and then solve it.

Answer.

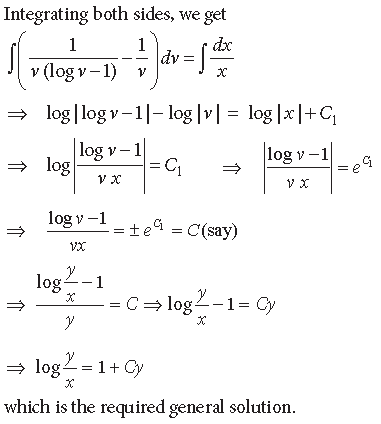
Long Answer Type Questions

Question. Find the particular solution of the differential

Answer.

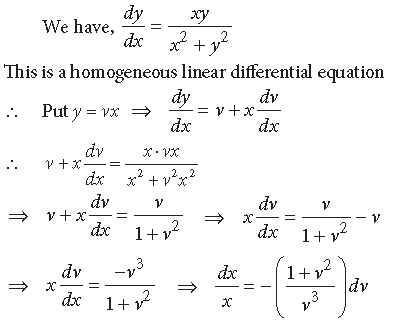
Question. Show that the differential equation

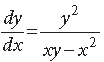
is homogeneous and also solve it.
Answer.

Question. Solve the following differential equation :

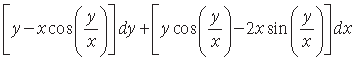
Answer. We have,

Question. Solve the following differential equation :

Answer.

Question. Solve the differential equation x² dy + (xy+y²)dx = 0 given y = 1, when x = 1
Answer. We have, x² dy + (xy + y²) dx = 0

Question. Solve the differential equation

Answer.