Matrices VBQs Class 12 Mathematics

VBQs Matrices Class 12 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 12 Mathematics with solutions. The following Matrices Class 12 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 12 examinations.

Matrices VBQs Class 12 Mathematics

Question.

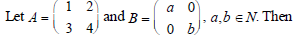
(a) there cannot exist any B such that AB = BA
(b) there exist more than one but finite number of B’s such that AB = BA
(c) there exists exactly one B such that AB = BA
(d) there exist infinitely many B’s such that AB = BA

Question. If A and B are square matrices of size n × n such that A² – B² = (A- B)(A+ B) , then which of the following will be always true?
(a) A = B
(b) AB = BA
(c) either of A or B is a zero matrix
(d) either of A or B is identity matrix

Question.

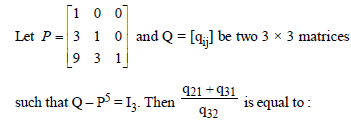
(a) 10
(b) 135
(c) 15
(d) 9

Question.

and B = A2⁰. Then the sum of the elements of the first column of B is?
(a) 211
(b) 210
(c) 231
(d) 251

Question.

then which one of the following statements is not correct?
(a) A² + I = A(A² – I)
(b) A⁴ – I = A² + I
(c) A³ + I = A(A³ – I)
(d) A³ – I = A(A – I)

Question. If

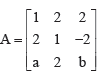
is a matrix satisfying the equation AA^T = 9I, where I is 3 × 3 identity matrix, then the ordered pair (a, b) is equal to:
(a) (2, 1)
(b) (–2, – 1)
(c) (2, – 1)
(d) (–2, 1)

Question. Let A and B be two symmetric matrices of order 3.
Statement-1: A(BA) and (AB)A are symmetric matrices.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.
(a) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
(b) Statement-1 is true, Statement-2 is false.
(c) Statement-1 is false, Statement-2 is true.
(d) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

Question. The number of all 3 × 3 matrices A, with enteries from the set {–1, 0, 1} such that the sum of the diagonal elements of AA^T is 3, is _______.

Question. Let A and B be any two 3 × 3 matrices. If A is symmetric and B is skewsymmetric, then the matrix AB – BA is:
(a) skewsymmetric
(b) symmetric
(c) neither symmetric nor skewsymmetric
(d) I or – I, where I is an identity matrix

Question.

(a) y = 2x
(b) y = – 2x
(c) y = x
(d) y = – x

Question. If

then AB equals
(a) I
(b) A
(c) B
(d) 0

Question. Let a be a root of the equation x² + x + 1 = 0 and the matrix

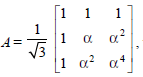
then the matrix A³¹ is equal to:
(a) A
(b) I₃
(c) A²
(d) A³

Question. For two 3 × 3 matrices A and B, let A + B = 2B^T and 3A + 2B = I₃, where B^T is the transpose of B and I₃ is 3 × 3 identity matrix. Then :
(a) 5A + 10B = 2I₃
(b) 10A + 5B = 3I₃
(c) B + 2A = I₃
(d) 3A + 6B = 2I₃

Question. The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is
(a) 5
(b) 6
(c) at least 7
(d) less than 4

Question.

where i = √-1, then which one of the following is not true?
(a) α ≤ α² + b² ≤ 1
(b) α² – d² = 0
(c) α² – c² = 1
(d) α² – b² = 1/2

Question. If ω ≠ 1 is the complex cube root of unity and matrix

(a) 0
(b) –H
(c) H²
(d) H

Question.

(a) 1/√5
(b) 1/√3
(c) 1/√2
(d) 1/√6

Question. If

then which one of the following holds for all n ≥ 1, by the principle of mathematical induction
(a) Aⁿ = nA – (n – 1) I
(b) Aⁿ = 2^n–1 A – (n – 1) I
(c) Aⁿ = nA + (n – 1) I
(d) Aⁿ = 2^n–1 A + (n – 1) I

Question. If

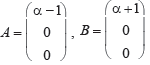
be two matrices, then AB^T is a non-zero matrix for |α| not equal to
(a) 2
(b) 0
(c) 1
(d) 3

Question.

then 10A^–1 is equal to:
(a) A – 4I
(b) 6I – A
(c) A – 6I
(d) 4I – A

Question. If p, q, r are 3 real numbers satisfying the matrix equation,

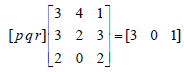
then 2p + q – r equals :
(a) – 3
(b) – 1
(c) 4
(d) 2

Question. The matrix A² + 4A – 5I, where I is identity matrix and

Question. If A is a symmetric matrix and B is a skew-symmetrix matrix such that

then AB is equal to :

Question.

is equal to __________.

Question.

Then a value of α is :
(a) π/32
(b) 0
(c) π/64
(d) π/16

Question.

(a) 2
(b) 3
(c) 6
(d) 4

Question. If

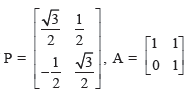
and Q = PAP^T, then P^T Q²⁰¹⁵ P is ;

Question.

(a) α = 2αb,β = a + b
(b) α = α² + b , β = αb
(c) α = α² + b , β = 2αb
(d) α = α² + b , β = α² – b²

Question. Let α, b, c ∈ R be all non-zero and satisfy α³ + b³ + c³ = 2. If the matrix

satisfies A^TA = I, then a value of αbc can be :
(a) − 1/3
(b) 1/3
(c) 3
(d) 2/3

CASE STUDY QUESTIONS

1.A manufacture produces three stationery products Pencil, Eraser and Sharpener which he sells in two markets.

Annual sales are indicated below 

If the unit Sale price of Pencil, Eraser and Sharpener are ₹ 2.50, ₹ 1.50 and ₹ 1.00 respectively, and unit cost of the above three commodities are ₹ 2.00, ₹ 1.00 and ₹ 0.50 respectively, then, based on the above information answer the following:

Question. Total revenue of market A
(a) ₹ 64,000
(b) ₹ 60,400
(c) ₹ 46,000
(d) ₹ 40,600

Question. Total revenue of market B
(a) ₹ 35,000
(b) ₹ 53,000
(c) ₹ 50,300
(d) ₹ 30,500

Question. Cost incurred in market A
(a) ₹ 13,000
(b) ₹ 30,100
(c) ₹ 10,300
(d) ₹ 31,000

Question. Profit in market A and B respectively are
(a) (₹ 15,000, ₹ 17,000)
(b) (₹ 17,000, ₹ 15,000)
(c) (₹ 51,000, ₹ 71,000)
(d) (₹ 10,000, ₹ 20,000)

Question. Gross profit in both market
(a) ₹ 23,000
(b) ₹ 20,300
(c) ₹ 32,000
(d) ₹ 30,200