Trigonometric Functions Class 11 Mathematics Important Questions

Please refer to Trigonometric Functions Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.

Class 11 Mathematics Important Questions Trigonometric Functions

Assertion & Reasoning Based MCQs

(a) Assertion and Reason both are correct statements and Reason is the correct explanation of Assertion.
(b) Assertion and Reason both are correct statements but Reason is not the correct explanation of Assertion.
(c) Assertion is correct statement but Reason is wrong statement.
(d) Assertion is wrong statement but Reason is correct statement.

Question. Assertion : The value of sin(–690°) cos(–300°) + cos(–750°)sin(–240°) = 1
Reason : The values of sin and cos is negative in third and fourth quadrant respectively.

Question. If A + B + C = 180°, then
Assertion : cos2A/2 + cos2 B/2 – cos C/2 = 2cos A/2 cos B/2 sin C/2
Reason : cos C + cosD = 2cos (C+D/2) cos (C-D/2)

Question. Assertion : The value of θ = π/3 or 2π/3 .
when q lies between (0, 2p) and sin²θ = 3/4 .
Reason : sinθ is positive in the first and second quadrant.

Question. Let secθ + tanθ = m, where 0 < m < 1.
Assertion : secθ = m2+1/2m and sinθ = m2-1/m2+1 Reason : θ lies in the third quadrant.

Question. Let a be α real number lying between 0 and π/2 and n be a positive integer.
Assertion : tana + 2tan²α+ 2²tan2²α + … + 2n–1 tan2n–1 a + 2n cot 2n α = cotα.
Reason : cotα – tanα = 2cot²α.

Very Short Answer Type Questions :

Question. Find the value of cos 240° + sin π/3 .
Answer: cos 240° + sin π/3 = cos (π+π/3) + sin π/3
= -cosπ/3 + sinπ/3 = -1/2 + √3/2 = √3-1/2

Question. Find the value of sin (-11π/3) .
Answer: sin (-11π/3) = -sin(11π/3) = -sin(4π-π/3) = sinπ/3 = √3/2 .

Question. What is the value of sin 31π/3 ?
Answer: sin 31π/3 = sin(10π + π/3) = sin π/3 = √3/2

Question. Express –47° 30′ in radian measure.
Answer: –47° 30′ = −(47, 30/60)° = – (47,1/2)° = – (95/2)° .
Now, 1° = (π/180)c ⇒ -(95/2)° = -(π/180 x 95/2)c =-(19π/72)c .

Question. Find the value of tan (31π/3) .
Answer: tan(31π/3) = tan (10π + π/3) = tan(π/3) = √3 .

Question. Find the value of cos (–1710°).
Answer: cos(–1710°) = cos 1710° = cos(19π/2) = 0

Question. Find the degree measure of 5π/12 radians.
Answer: 5π/12 radians = 5π/12 x 180/π degrees = 75°

Question. Convert 4 radians into degree measure.
Answer: 4 radians = (4 x 180/π)° = (4 x 180 x 7/22)°
= 229 1/11 degree = 229° + 1 x 60/11 minute
= 229° + 5′ + 5/11 minute = 229° + 5′ + 27.2′′
Hence, 4 radians = 229°5′27′′ approx.

Question. Write 13π/4 radians in the degrees.
Answer: 13π/4 radians = (13π/4 x 180/π)° = 585°

Question. Find the radian measure of 625°.
Answer: 625° = (625 x π/180)c = 10.91 radian (∴ 1° = π/180 radian)

Short Answer Type Questions :

Question. If 5 sin x = 3, x lies in 1st quadrant, then find the value of sec x – tan x/sec x + tan x .
Answer: We have, 5 sin x = 3 ⇒ sin x = 3/5
Since, sin² x + cos² x = 1
⇒ cos² x = 1 – sin2 x = 1-9/25 = 16/25 .
⇒ cos x = 4/5
∴ sec x = 5/4 and tan x = (3/5 x 5/4) = 3/4 
Hence, sec x – tan x/sec x – tan x = 5/4 – 3/4 / 5/4+3/4 = 2/4 x 4/8 = 1/4

Question. If sin x = 3/5 , π/2 < x <π , then find the value of cos x, tan x, sec x and cot x.
Answer: sinx = 3/5 and π/2< x <π
⇒ x belongs to second quadrant.
Since, sin² x + cos² x = 1 ⇒ cos² x = 1-9/25 = 16/25 
⇒ cosx = − 4/5 , tanx = -3/4 , secx = − 5/4 , cot x = -4/3

Question. Prove that cos2(45° + x) – sin2(45° – x) is independent of x.
Answer: cos2(45° + x) – sin2(45° – x)
= cos[(45° + x) + (45° – x)]cos[(45° + x) – (45° – x)]
[∴ cos²A – sin²B = cos(A + B) cos(A – B)]
= cos 90° cos 2x = (0) cos 2x = 0
which does not contain x and hence is independent of x.

Question. Write the value of √2+√2+2cos θ in the simplest form.
Answer: √2+√2+2cos θ = √2+√2(1+cosθ)

Question. If the angles of a triangle are in the ratio 3 : 4 : 5, then find the smallest angle in degree and the greatest angle in radians.
Answer: Let the three angles be 3x, 4x and 5x degrees, then
3x + 4x + 5x = 180° ⇒ 12x = 180° ⇒ x = 15°
∴ Smallest angle 3x = 45° and greatest angle = 5x = 75°
= 75 x π/180 radians = 5π/12 radians

Question. Find the value of cos 55° + cos 125° + cos 300°.
Answer: cos 55° + cos 125° + cos 300°
= 2 cos 90° cos 35° + cos (360° – 60°)
= 0 + cos 60° = 1/2

Question. Find the value of sin(n + 1) x ⋅ sin (n + 2) x + cos (n + 1) x ⋅ cos (n + 2)x.
Answer: sin(n + 1)x ⋅ sin (n + 2)x + cos (n + 1) x ⋅ cos (n + 2)x
= cos [(n + 2)x – (n + 1)x] = cos x
[Applying cos (A – B) = cos A cos B + sin A sin B]

Question. Show that :

Answer:

Question. If the arcs of the same lengths in two circles subtend angles 65° and 110° at the centre, find the ratio of their radii.
Answer: Let radii of circles be r1 and r2.
Given θ₁ = 65° ⇒ θ₁ = (65π/180)c
and θ₂ = 110° ⇒ θ₂ = (110π/180)c
Also length of arcs are same
∴ θ₁r₁ = θ2r₂
65π/180 r1 = 110π/180 r₂ ⇒ r₁/r₂ = 110/65 = 22/13
⇒ r₁ : r₂ = 22 : 13

Question. Prove that cos 20° cos 40° cos 80° = 1/8 .
Answer: L.H.S. = cos 20° cos 40° cos 80°
= cos 20° cos(60° – 20°) cos(60° + 20°)
= cos 20° (cos 60° cos 20° + sin 60° sin 20°)
(cos 60° cos 20°– sin 60° sin 20°)

Question. Prove that 16 sin5θ – 20 sin3θ + 5 sin θ = sin 5θ
Answer: L.H.S. = 16 sin5 θ – 20 sin3 θ + 5 sin θ
= 16 sin5 θ – 16 sin3 θ – 4 sin3 θ + 5 sin θ + 3 sin θ – 3 sin θ
= 16 sin3 θ[sin2 θ – 1] + sin 3θ + 2 sin θ
= –16 sin3 θ cos2 θ + sin 3θ + 2 sin θ
= –(2 sin θ cos θ)2 ⋅ 4 sin θ + sin 3θ + 2 sin θ
= –4 sin2 2θ sin θ + sin 3q + 2 sin θ
= 2 sin θ[1 – 2 sin2 2θ] + sin 3θ
= 2 sin θ cos 4q + sin 3θ
= sin 5θ + sin(–3q) + sin 3θ = sin 5θ = R.H.S.

Question. Prove that :
cos⁴ π/8 + cos⁴ 3π/8 + cos⁴ 5π/8 + cos⁴ 7π/8 = 3/2 .
Answer:

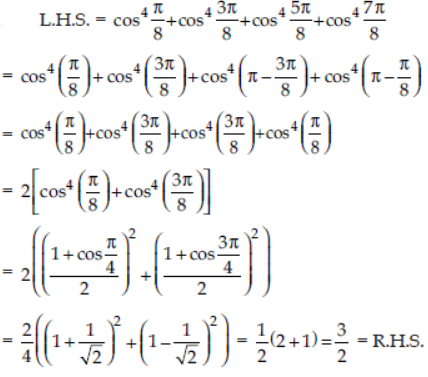
Question. Express the following as a sum or difference :
2 sin 5θ/2 cos 7θ/2 .
Answer: 2sin 5θ/2 cos 7θ/2 = sin(5θ/2 + 7θ/2) + sin(5θ/2 – 7θ/2)
[∴ 2 sin A cos B = sin(A + B) + sin(A – B)]
= sin 6θ + sin(–θ) = sin 6θ– sin θ [∴ sin(–θ) = –sin θ]

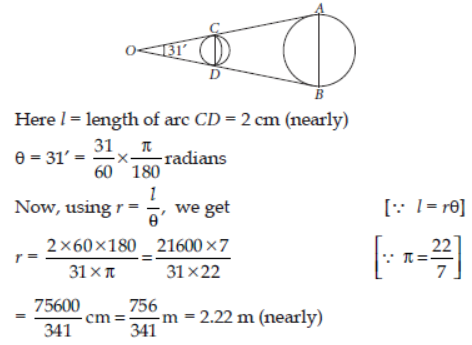
Question. Find the distance from the eye at which a coin of diameter 2 cm should be held so as just to conceal the full moon whose angular diameter is 31′.
Answer: Let AB be the diameter of the moon and O, the eye of the observer so that ∠AOB = 31′. Let CD be the diameter of the coin. The full moon will be just concealed if the diameter of a coin also subtends the same angle as the diameter of the moon at O, i.e., if ∠COD = 31′. As ∠COD is small, CD may be treated as the arc of a circle whose centre is O and radius = OC or OD, the distance of coin from O. Let OC = OD = r

Question. Find the value of m sin x + n cos x, if tan x/2 = m/n .
Answer: We have, tan x/2 = m/n

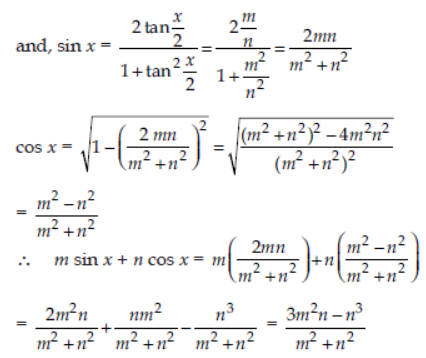
Question. A horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight and describes 88 metres when it has traced out 72° at the centre, find the length of the rope.
Answer: Let the post be at point P and let PA be the length of the rope in tight position. Suppose the horse moves along the arc AB so that arc AB = 88 m, and let r be the length of the rope i.e., PA = r 22
Now, θ = 72° = (72 x π/180) radian
= (2π/5) radian
θ =arc/radius ⇒ 2π/5 = 88/r
⇒ r = 88 × 5/2π = 70m

Question. Find the value of sin π/18 + sin π/9 + sin 2π/9 + sin 5π/18 .
Answer:

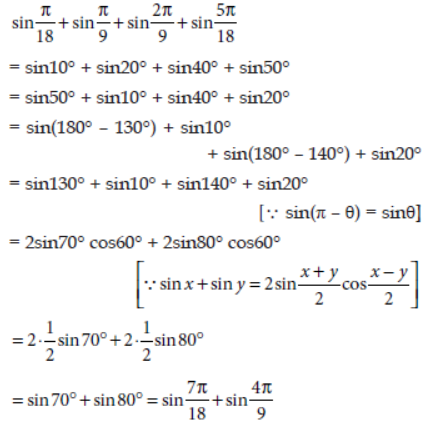
Question. Prove that : tan 4x = 4tan x (1-tan2 x)/1-6 tan2 x + tan4 x .
Answer: L.H.S. = tan 4x = tan(2(2x))

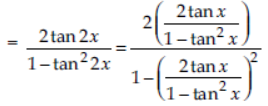
Question. Prove that :
(sin 3x + sin x) sin x + (cos 3x –cos x) cos x = 0
Answer: Consider,
L.H.S. = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
= sin 3x sin x + sin²x + cos3x cos x –cos²x
= (cos 3x cosx + sin 3x sin x) – (cos2x – sin2x)
= cos(3x – x) – cos 2x
[Using cos (A – B) = cos A cos B + sin A sin B
and cos²θ – sin2θ = cos2θ]
= cos 2x – cos 2x = 0 = R.H.S.

Question. Prove that :
sin A – sin 3A + sin5A – sin7A/cos A – cos 3A + cos5A – cos7A = cot 2A
Answer: Consider,

Question. Prove that : 2cos π/13 cos 9π/13 + cos 3π/13 + cos 5π/13 = 0 .
Answer: Consider,

Question. If tan x = π < x < 3π/2 , find the value of sin x/2 , cos x/2 , tan x/2 .
Answer: Given, tanx = 3/4 , π < x < 3π/2
⇒ π/2 < x/2 < 3π/4
Therefore sin x/2 is positive and cos x/2 is negative.

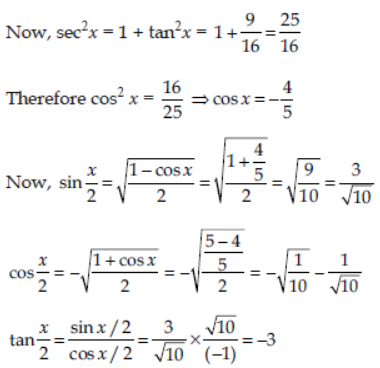
Question. Prove that : (cos x – cos y)2 + (sin x – sin y)2 = 4 sin² x-y/2 .
Answer: L.H.S = (cos x – cos y)² + (sin x – sin y)²
= cos² x + cos² y + sin² x + sin² y – 2 cos x cos y – 2sin x sin y
= 2 – 2 cos x cos y – 2 sin x sin y
= 2 – 2 [cosx cos y + sin x sin y]
= 2 – 2 cos(x – y) = 2(1 – cos(x –y))
= 4 sin2 (x-y/2) = R.H.S.

Question. Prove that : 
cos² x + cos²(x+π/3) + cos² (x-π/3) = 3/2
Answer:

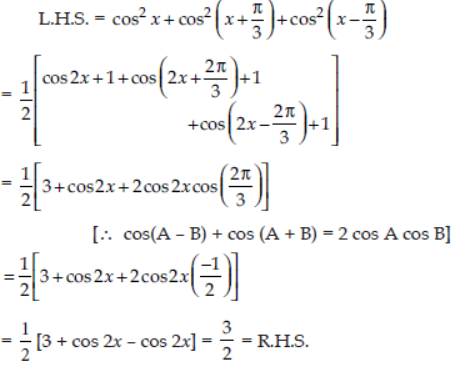
Question. Prove that : 1+sin x – cos x/1+sin x + cos x = tan x/2 .
Answer: L.H.S. = 1+sin x – cos x/1+sin x + cos x

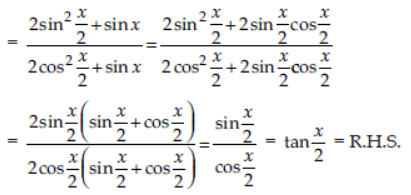
Long Answer Type Questions :

Question. Prove that : sin x + sin y + sin z – sin (x + y + z) = 4 sin x+y/2 sin y+z/2 sin x+z/2 .
Answer: L.H.S. = (sin x + sin y) + (sin z – sin(x + y + z))

Question. If A, B, C, D be the angles of a cyclic quadrilateral, taken in order, prove that
(i) cos A + cos B + cos C + cos D = 0
(ii) cos(180° + A) + cos(180° + B) + cos(180° + C) – sin(90° + D) = 0.
Answer: (i) Since A, B, C, D are the angles of a cyclic
quadrilateral, we have
A + C = 180° and B + D = 180°
⇒ cos A = cos(180° – C) and cos B = cos(180°– D)
⇒ cos A = –cos C …(i)
and cos B = –cos D …(ii)
[Q cos(180° – q) = – cos q]
Addition. (i) & (ii), we get
cos A + cos B = –(cos C + cos D)
⇒ cos A + cos B + cos C + cos D = 0
(ii) L.H.S. = –cos A – cos B – cos C – cos D
= –cos A – cos B – cos(180° – A) – cos(180° – B)
= –cos A – cos B – (–cos A) – (–cos B)
= –cos A – cos B + cos A + cos B = 0 = R.H.S.

Question. Find the value of cos π/5 cos 2π/5 cos 4π/5 cos 8π/5 .
Answer: cos π/5 cos 2π/5 cos 4π/5 cos 8π/5

Question. Prove that : 
sin³ x + sin³ (2π/3 + x) + sin³ (4π/3 + x) = – 3/4 sin 3x .
Answer:

Question. If x cosθ = y cos(θ + 2π/3) = z cos (θ + 4π/3) prove that xy + yz + zx = 0.
Answer: Note that xy + yz + zx = xyz (1/x + 1/y + 1/z)
If we put x cos q = y cos (θ+2π/3)
= zcos ((θ+4π/3) = k(say)

Case Based Questions :

Case I : Read the following passage and answer the questions from 41 to 45.
Nitish is playing with Pinwheel toy which he bought from a village fair. He noticed that the pinwheel toy revolves as fast as he blows it.

Consider the Pinwheel toy makes 360 revolutions per minute.

Question. Angle made by Pinwheel toy (in degree) in 6 revolutions is
(a) 2630°
(b) 2160°
(c) 2360°
(d) 2610°

Question. The value of 1° in radians is equal to
(a) π/170
(b) π/120
(c) π/180
(d) π/60

Question. Angle made by Pinwheel toy (in radians) in 6 revolutions is
(a) 12π
(b) 14π
(c) 16π
(d) 10π

Question. The number of revolutions made by Pinwheel toy in 120 seconds is
(a) 720
(b) 120
(c) 240
(d) 360

Question. The number of revolutions made by Pinwheel toy in 1 sec is
(a) 7
(b) 9
(c) 6
(d) 8

Case II : Read the following passage and answer the questions from 46 to 50.
Sudhir who is a student of class XI got a Maths assignment from his class teacher.
He did all the questions except a few. If the value of sin x = 3/5 and cos y = – 12/13 , where x and y both lie in second quadrant then help Sudhir in solving these questions.

Question. The value of sin(x + y) equals
(a) -56/65
(b) 56/65
(c) 55/67
(d) -55/67

Question. Find the value of sin 75°.
(a) 1-√3/√2
(b) 1+√3/2√2
(c) 1-√3/2√2
(d) 1+√3/2

Question. What will be the value of cos x?
(a) 4/5
(b) -3/5
(c) -4/5
(d) 3/5

Question. What will be the value of siny ?
(a) 5/12
(b) -12/13
(c) -5/13
(d) 5/13

Question. Which of the following options is correct?
(a) sin (x – y) = sinx cosy + cosx siny
(b) sin (x + y) = cosx siny – sinx cosy
(c) sin (x + y) = sinx cosy + cosx siny
(d) sin (x – y) = sinx siny – cosx cosy

Case III : Read the following passage and answer the questions from 51 to 55.
Arvind and Murli came to Delhi from Mumbai for an official work. They decided to explore one of the tallest minaret of worldi.e., Qutab Minar. 
The angle of elevation of Arvind’s eyes from a point A to the top of Minaret is 75°. Another point B which is 400 metres far from the Qutab Minar. Given that height of the Minaret is 73 metres.

Question. How long a wire is needed to tied between the top of Minaret and the point A ?
(a) 73/√3+1 metres
(b) 146√2/(√3+1) metres
(c) 73√2/(√3+1) metres
(d) 73(2-√3) metres

Question. What is the distance between point A to B?
(a) 173/(√3+1) metres
(b) 73√2/(√3+1) metres
(c) 400-146/(√3+1)² metres
(d) 800+73(√3-1)²/2 metres

Question. What is the value of angle C?
(a) 105° – tan-1(73/400)
(b) 180° – tan-1(73/400)
(c) 105° + tan-1(73/400) 
(d) None of these

Question. The angle of elevation (in degrees) from point B to the top of the Minaret is
(a) ∠B =tan-1(400/73) 
(b) ∠B sin-1(400/73) 
(c) ∠C = cos-1(400/73) 
(d) ∠B tan-1(400/73) 

Question. What is the distance of a point A from the foot of Minaret?
(a) 146/(√3+1)²metres
(b) 73/(√3+1)²metres
(c) 73/(√2+1)²metres
(d) 73(√3-1)²/2 metres