Please refer to Surface areas and Volumes Class 9 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 9 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 9 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 9.
Class 9 Mathematics Important Questions Surface areas and Volumes
Very Short Answer Type Questions:
Question. The radius of a circular cylinder is same as that of a sphere. Their volumes are equal. Then find height of the cylinder.
Ans.Let h be the height of cylinder.
Radius of cylinder = Radius of sphere = r
Then, we have 4/3πr3 = πr2h ⇒ h = 4/3r
∴ Height of cylinder = 4/3 times its radius.
Question. If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
Ans. If sphere is completely inscribed in a cube then edge of cube is the diameter of sphere.
Let a be the edge of cube.
So a is the diameter of sphere

⇒ Volume of cube = (a3)
Volume of sphere =4/3 π(a/2)3
∴ Required ratio = a3/4/3 π(a3/8) = a3: π/6 a3 = 6: π
Question. The dimensions of an open box are 52 cm, 40 cm and 29 cm. Its thickness is 2 cm. If 1 cm3 of metal used in the box weighs 0.5 gms, then find the weight of the box.
Ans. Volume of metal
= (52 × 40 × 29 – 48 × 36 × 27) cm3 = 13664 cm3
∴ Weight of the box = (13664 × 0.5/1000) kg = 6.832 kg
Question. If the radius of a sphere is doubled, what is the ratio of the volume of the first sphere to that of the second sphere.
Ans. Let the old radius be r.
Then, new radius = 2r
Volume of old sphere = 4/3 πr3
Volume of new sphere = 4/3 π(2r)3
= 4/3π× 8r3 = 32 πr3
∴ Required ratio = 4/3πr3 : 32/3πr3 = 1 : 8
Question. A teak wood log is in the form of a cuboid of volume 76800 m3. How many rectangular planks of size 40 m × 12 m × 20 m can be cut from the cuboid?
Ans. Number of rectangular planks
= Volume of cuboid of wood log/Volume of one plank = 76800/40 ×12 × 20 = 8
Short Answer Type Questions:
Question. A right triangle, with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm and 5 cm respectively. Find the ratio of the total surface areas of two cones so formed.
Ans. Let S1 and S2 be the total surface areas of two cones so formed by revolving about side 12 cm and 5 cm respectively.
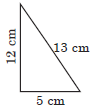
Total surface area of a cone = πr(l + r)
∴ S1 = π(5) (13 + 5) = 90π cm2
S2 = π(12) (12 + 13) = 300π cm2
∴ Required ratio = S1/S2 = 90π/300π = 3:10
Question. The radius of the circular part of a hemispherical bowl is 9 cm. Find the total capacity of 21 such bowls.
Ans. Volume of one bowl = Volume of hemisphere
= 2/3 πr3 = (2/3 × 22/7 × 93) cm3
Capacity of 21 such bowls = 21 × 2/3 × 22/7 × 93
= 32076 cm3
Question. If the height of a cylinder is 11 cm and area of curved surface is 968 sq. cm. Find the radius of the cylinder.
Ans. Height of cylinder = 11 cm
Curved surface area = 968 cm2
⇒ 2πrh = 968
⇒ 2 × 22/7 × π ×11 = 968 ⇒ r = 14 cm
Question. A closed cuboidal tank can store 5040 litres of water. The external dimensions of the tank are 2.2 m × 1.7 m × 1.7 m. If the walls of the tank are 5 cm thick, then what is the thickness of the bottom (top) of the tank if they are same?
Ans. Capacity of tank = 5040 litres
= 5040/1000 m3 = 5.040m3
Internal length of tank = (2.2 − 2 × 5/100)m = 2.1m
Internal breadth of tank = (1.7 − 2 × 5/100)m = 1.6 m
Let the thickness of tank in the bottom be x m.
∴ Internal height of tank = (1.7 – 2x) m
Now, Internal volume of tank = Capacity of tank
⇒ 2.1 × 1.6 × (1.7 – 2x) = 5.040
⇒ 1.7 – 2x = 5.040/2.1 × 1.6 = 1.5
⇒ 2x = 1.7 – 1.5 = 0.2
⇒ x = 0.1 m = 0.1 × 100 cm = 10 cm
So, required thickness = 10 cm
Question. Find the length of cloth used for making a cone of height 2 times the base radius, which is square of 2, if the cloth is l00p m wide.
Ans. Let r and h be the radius and height of cone respectively.
⇒ h = 2r and r = 4 m ⇒ h = 8 m
l = √r2+ h2 = √(4)2 + (8)2 = √16 + 64 = √80 cm
Lateral or curved surface area = πrl
= π × 4 × √80 = 16√5 π m2
∴ Length of cloth = 16√5π / 100π m = 0.36 m = 36 cm
Question. Find the volume of a lead pipe 3.5 m long, if the external diameter of the pipe is 2.4 cm, thickness of lead is 3 mm and 1 cm3 of lead weighs 12 g.
Ans. External diameter of the pipe = 2.4 cm
External radius of the pipe, (R) = 2.4/2cm =1.2 cm
Thickness of the pipe = 3 mm = 0.3 cm
Internal radius, (r) = External radius – thickness
= 1.2 cm – 0.3 cm = 0.9 cm
Length of the pipe (h) = 3.5 m = 350 cm
Volume of lead = π(R2 – r2)h
= 22/7 × [(1.2)2– (0.9)2] × 350 = 22/7 × 0.63 × 350 = 693 cm3
Question. The dome of a building is in the form of a hemisphere. If its radius is 14 cm, find the cost of painting it at the rate of Rs 3 per sq. cm.
Ans. Since the dome of building is in the shape of hemisphere
⇒ Curved surface area of dome = 2πr2
= 2 ×22/7 × 14 × 14 = 2 × 22 × 2 × 14 = 1232 cm2
Cost of painting the dome at the rate of 1 sq. cm = Rs 3
∴ Cost of painting of 1232 cm2 dome
= Rs 3 × 1232 = Rs 3696
Question. A cube of 8 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of its base are 17 cm and 14 cm. Find the rise in water level in the vessel.
Ans. Edge of the cube = 8 cm
∴ Volume of the cube = a3 = (8)3 = 512 cm3
If the cube is immersed in the vessel, then the water level rises. Let the rise in water level be x.
Clearly, Volume of the displaced water = Volume of the cube
⇒ Volume of the cube = 17 cm × 14 cm × x cm
⇒ 512 = 17 × 14 × x
⇒ x = 512/17 × 14
⇒ x = 512/238 = 2.15 cm
Question. The slant height of a cone is 25 cm and the vertical height is 24 cm. Find the radius and the total surface area of the cone.
Ans. Here, h = 24 cm and slant height (l) = 25 cm
Let r be the radius of cone. Then,
l2 = h2 + r2
⇒ r2 = 252 – 242 = 49 ⇒ r = 7
Total surface area of the cone = πr(l + r)
= [22/7 × 7 × (25 +7)] cm2 = 704 cm2.
Question. The base of a cubical box has a perimeter 250 m. Find the cost of painting its lateral surface area at the rate of Rs 10 per m2.
Ans. Let the side of cubical box be a m.
Perimeter of base of a cubical box = 4a m
⇒ 250 = 4a ⇒ a = 62.5 m
Now, LSA of cubical box = 4a2 = 4 × (62.5)2 = 15625 m2
Cost of painting 1 m2 = Rs 10
∴ Total cost of painting = 15625 × 10 = Rs 156250.
Question. On a construction site, a deep pit is barricaded from the remaining portion by using 100 hollow cones. Each one has a base diameter 20 cm and height half a meter. What is the cost of painting the outer surface of all the cones, if cost of painting is Rs 30 per m2?
[Use, π = 3.14, √26 = 5.1]
Ans. Radius of cone, r = 20/2 = 10 cm = 0.1 m
Height of cone, h = 1/2 m
Slant height of cone, l = √h2 + r2
⇒ l = √(1/2)2 + (0.1)2 ⇒ √26/100 = 5.1/10 = 0.51m
Curved surface area of 100 cones = (100 × πrl)m2
= (100 × 3.14 × 0.1 × 0.51)m2= 16.014 m2
Total cost of painting = 30 × 16.014 = Rs 480.42
Question. Two cones have their heights in the ratio 1 : 4 and radii of their bases in the ratio 4 : 1. Find the ratio of their volumes.
Ans. Let the heights of the cones be h and 4h and radii of their bases be 4r and r and V1 and V2 are their respective volumes.
∴ V1 = 1/3π(4r)2 h = 16/3πr2h , V2 = 1/3π(r)2 4h = 4/3πr2h
⇒ V1/ V2 = 16/3πr2h / 4/3πr2h = 4/1 ⇒ V1 : V2 = 4 : 1
Question. Find the total surface area, lateral surface area and the length of diagonal of a cube, each of whose edges measues 20 cm. (Take √3 = 1.732)
Ans. Here, side (a) = 20 cm
∴ Total surface area of the cube = 6a2 = 6(20)2
= 2400 cm2
and, lateral surface area of the cube = 4a2 = 4(20)2
= 1600 cm2
Also, length of diagonal of a cube = √3a
= √3 × 20= (1.732 × 20) = 34.64 cm.
Long Answer Type Questions:
Question. Three identical cylinders of base radius r units and height h units is placed one above the other to form a new cylinder. Find the ratio (in terms of r and h) of the curved surface area to the total surface area of the cylinder thus formed.
Ans. Since, three identical cylinders of radius r units and height h units are place one above the other.
∴ Height of cylinder thus formed
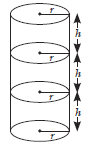
= 3 × h = 3h units
And radius of new cylinder = r units
∴ CSA of new cylinder = 2πr(3h)
= 6πrh sq. units
And TSA of new cylinder = 2πr(r + 3h) sq. units
Now, required ratio = 6πrh/2πr(r + 3h) = 3h/r+3h
or 3h : (r + 3h).
Question. The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost of painting one sq. cm of the surface is 7 paise. Find the total cost to paint the vessel all over. (Ignore the area of edge)
Ans. Let R cm and r cm be respectively the external and internal radii of the hemispherical vessel.
Then, R = 12.5 cm, r = 12 cm.
Now, External surface area of the vessel
= 2πR2 = 2 × 22/7 × (12.5)2
Internal surface area of the vessel = 2πr2
= 2 × 22/7 × (12)2
∴ Total area to be painted
= 2 × 22/7 × (12.5)2 + 2 × 22/7 × 122
= 2 × 22/7 × {(25/2)2 +122}
= 2 × 22/7 × (625/4 + 144) = 13211/7 cm2
Cost of painting at the rate of 7 paise per sq. cm
= Rs (13211/7 × 7/100) = Rs 132.11
