Please refer to Relations and Functions Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Mathematics Important Questions Relations and Functions
Very Short Answer Type Questions
Question. If R = {(x, y) : x + 2y = 8} is a relation on N, write the range of R.
Answer. Here, R = {(x, y) : x + 2y = 8}, where x, y ∈ N.
For x = 1, 3, 5, …
x + 2y = 8 has no solution in N.
For x = 2, we have 2 + 2y = 8 ⇒ y = 3
For x = 4, we have 4 + 2y = 8 ⇒ y = 2
For x = 6 , we have 6 + 2y = 8 ⇒ y = 1
For x = 8, 10, …
x + 2y = 8 has no solution in N.
∴ Range of R = {y : (x, y) ∈ R} = { 1, 2, 3}
Question. Let R = {(a, a3) : a is a prime number less than 5} be a relation. Find the range of R.
Answer. Given relation is
R = {(a, a3) : a is a prime number less than 5}.
∴ R = {(2, 8), (3, 27)}
So, the range of R is {8, 27}.
Question. Let R be the equivalence relation in the set
A = {0, 1, 2, 3, 4, 5} given by
R = {(a, b) : 2 divides (a – b)}. Write the equivalence class [0].
Answer. Here, R = {(a, b) ∈ A × A : 2 divides (a – b)}
This is the given equivalence relation, where
A = {0, 1, 2, 3, 4, 5}
∴ [0] = {0, 2, 4}.
Question. State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
Answer. For transitivity of a relation,
If (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
We have, R = {(1, 2), (2, 1)}
(1, 2) ∈ R and (2, 1) ∈ R but (1, 1) ∉ R
∴ R is not transitive.
Question. State whether the function f : N → N given by f(x) = 5x is injective, surjective or both.
Answer. We have, f(x) = 5x
For x1, x2 ∈ N.
Let f(x1) = f(x2) ⇒ 5x1 = 5x2 ⇒ x1 = x2
∴ The function is one-one.
Now, f(x) is not onto. Since, for 2 ∈ N (co-domain),
there does not exist any x ∈ N (domain) such that
f(x) = 5x = 2
∴ f(x) is injective but not surjective.
Question. Let f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3} given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Answer. Here, f = {(1,2), (3, 5), (4, 1)}
⇔ f(1) = 2; f(3) = 5; f(4) = 1 …(1)
g = {(1, 3), (2, 3), (5, 1)}
⇔ g(1) = 3; g(2) = 3, g(5) = 1 …(2)
Now, gof : {1, 3, 4} → 1, 3}
Using (1) and (2), we get
(gof) (1) = g(f(1)) = g(2) = 3
(gof) (3) = g(f(3)) = g(5) = 1
(gof) (4) = g(f(4)) = g(1) = 3
∴ gof = {(1, 3), (3, 1), (4, 3)}.
Question. If f : R → R defined as
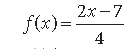
is an invertible function, write f–1(x).
Answer.
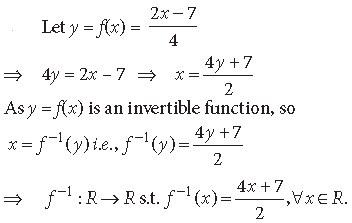
Question. If f : R → R is defined by f(x) = (3 – x3)1/3, then find fof(x).
Answer. f : R → R and f(x) = (3 – x3)1/3
∴ fof(x) = f(f(x)) = f [3 – x3)1/3]
= [3 – {(3 – x3)1/3}3]1/3
= [3 – (3 – x3)]1/3 = (3 – 3 + x3)1/3 = x
Question. If f : R → R is defined by f (x) = 3x + 2, find f (f (x)).
Answer. We have, f(x) = 3x + 2
∴ f (f (x)) = f (3x + 2) = 3(3x + 2) + 2 = 9x + 8
Question. If the function f : R → R, defined by f (x) = 3x – 4, is invertible, find f–1.
Answer. We have, f(x) = 3x – 4
Let f(x) = y ⇒ x = f–1(y)

Question. If f : R → R defined by f (x) = 3x + 5/2 is an invertible function, find f–1.
Answer.
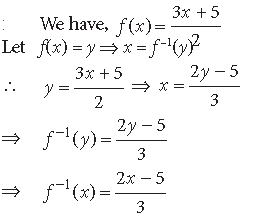
Question. Let * be a binary operation defined by a * b = 3a + 4b – 2. Find 4 * 5.
Answer. Here a * b = 3a + 4b – 2
∴ 4 * 5 = 3(4) + 4(5) – 2 = 12 + 20 – 2 = 30
Question. If the binary operation * on the set of integers Z is defined by a * b = a + 3b2, then find the value 2 * 4.
Answer. Here a * b = a + 3b2
∴ 2 * 4 = 2 + 3(4)2 = 2 + 3 × 16 = 50
Question. Let * be a binary operation on N given by a * b = H.C.F. (a, b); a, b ∈ N. Write the value of 22 * 4.
Answer.
Question. Let * be a binary operation on set Q of rational numbers defined as a * b = ab/5 write the identity for *, if any.
Answer. Here a * b = H.C.F. (a, b)
∴ 22 * 4 = H.C.F. (22, 4) = 2
Short Answer Type Questions
Question. Let n be a fixed positive integer. Define a relation R in Z as follows ∀ a, b ∈ Z, aRb if and only if a – b is divisible by n. Show that R is an equivalence relation.
Answer. Given that, ∀ a, b ∈Z, aRb if and only if a – b is divisible by n.
Now,

Question. Let C be the set of complex numbers. Prove that the mapping f : C → R given by f (z) =| z|, ∀ z ∈ C, is neither one-one nor onto.
Answer. The mapping f :C → R

So, f( z) is not one-one. Also, f( z) is not onto as there is no pre-image for any negative element of R under the mapping f( z).
Question. Let R be a relation defined on the set of natural numbers N as follow :
R = {(x, y) x ∈ N, y ∈ N and 2x + y = 24}
Find the domain and range of the relation R.
Also, find if R is an equivalence relation or not.
Answer. Here, R = {(x, y) | x ∈ N, y ∈ N and 2x + y = 24}
Domain of R = {1, 2, 3, 4, …, 11}
Range of R = {2, 4, 6, 8, 10, 12 ,…, 22}
R is not reflexive as if (2, 2) ∈ R
⇒ 2 x 2 + 2 = 6 ≠ 24
In fact R is neither symmetric nor transitive.
⇒ R is not an equivalence relation.
Question. Show that the relation S in the set R of real numbers defined as S = {(a, b) : a, b ∈ R and a ≤ b3} is neither reflexive, nor symmetric, nor transitive.
Answer. We have S = {(a, b) : a ≤ b3} where a, b ∈ R.
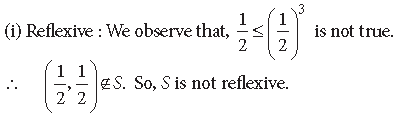
(ii) Symmetric : We observe that 1 ≤ 33 but 3 ≤ 13
i.e., (1, 3) ∈ S but (3, 1) ∉ S. So, S is not symmetric.
(iii) Transitive : We observe that, 10 ≤ 33 and 3 ≤ 23
but 10 ≤ 23
i.e., (10, 3) ∈ S and (3, 2) ∈ S but (10, 2) ∉ S
So, S is not transitive.
∴ S is neither reflexive, nor symmetric, nor transitive
Question. Let Z be the set of all integers and R be the relation on Z defined as R = {(a, b) : a, b ∈ Z and (a – b) is divisible by 5}. Prove that R is an equivalence relation.
Answer. We have R = {(a, b) : (a – b) is divisible by 5}
(i) Reflexive : For any a ∈ Z,
a – a = 0, which is a multiple of 5.
⇒ (a, a) ∈ R
Hence, R is reflexive.
(ii) Symmetric : For any a, b ∈ Z, let (a, b) ∈ R
⇒ (a – b) is a multiple of 5.
⇒ (a – b) = 5m, m ∈ Z ⇒ (b – a) = –5m
∴ (a, b) ∈ R ⇒ (b, a) ∈ R
Hence, R is symmetric.
(iii) Transitive : For any a, b, c, ∈ Z, let (a, b) ∈ R and
(b, c) ∈ R
⇒ (a – b) = 5m and (b – c) = 5n; m, n ∈ Z
⇒ a – b + b – c = 5m + 5n; m, n ∈ Z
⇒ a – c = 5(m + n); m, n ∈ Z
∴ a – c is a multiple of 5.
i.e., (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
Hence, R is transitive.
∴ R is an equivalence relation.
Question. Show that the relation S in the set
A = {x ∈ Z : 0 ≤ x ≤ 12} given by
S = {(a, b) : a, b ∈ Z, |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1.
Answer. We have, A = {x ∈ Z : 0 ≤ x ≤ 12}
∴ A = {0, 1, 2, 3, …, 12}
and S = {(a, b) : |a – b| is a multiple of 4}
(i) Reflexive : For any a ∈ A,
|a – a| = 0 is a multiple of 4.
Thus, (a, a) ∈ S
∴ S is reflexive.
(ii) Symmetric : For any a, b ∈ A,
Let (a, b) ∈ S
⇒ |a – b| is a multiple of 4
⇒ |b – a| is a multiple of 4 ⇒ (b, a) ∈ S
i.e., (a, b) ∈ S ⇒ (b, a) ∈ S
∴ S is symmetric.
(iii) Transitive : For any a, b, c ∈ A,
Let (a, b) ∈ S and (b, c) ∈ S
⇒ |a – b| is a multiple of 4 and |b – c| is a multiple of 4
⇒ a – b = ± 4k1 and b – c = ± 4k2; k1, k2 ∈ N
⇒ (a – b) + (b – c) = ± 4 (k1 + k2); k1, k2 ∈ N
⇒ a – c = ± 4 (k1 + k2); k1, k2 ∈ N
⇒ |a – c| is a multiple of 4 ⇒ (a , c) ∈ S
∴ S is transitive.
Hence, S is an equivalence relation.
The set of elements related to 1 is {5, 9}.
Question. Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
Answer. Here R = {(a, b) : b = a + 1}
= {(a, a + 1) : a, a + 1 ∈ {1, 2, 3, 4, 5, 6}}
= {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}
(i) R is not reflexive as (a, a) ∉ R ∀ a.
(ii) R is not symmetric as (1, 2) ∈ R but (2, 1) ∈ R.
(iii) R is not transitive as (1, 2) ∈ R, (2, 3) ∈ R but
(1, 3) ∈ R.
Question. Show that f : N → N, given by
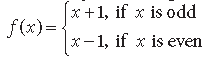
is both one-one and onto.
Answer. Here, f : N → N s.t.

Let x, y ∈ N s.t. f(x) = f(y)
We shall show that x = y
(i) If x and y both are even
f(x) = f(y) ⇒ x – 1 = y – 1 ⇒ x = y
(ii) If x and y both are odd
f(x) = f(y) ⇒ x + 1 = y + 1 ⇒ x = y
(iii) If x is odd and y is even
f(x) = f(y) ⇒ x + 1 = y – 1
⇒ y – x = 2 …(1)
R.H.S. is even but L.H.S. is odd.
⇒ Equation (1) in N is not possible.
⇒ (iii) does not arise.
(iv) If x is even and y is odd, does not arise. In any case, f(x) = f(y) ⇒ x = y
⇒ f is one-one
For any y ∈ N (co-domain), y can be even or odd When y is odd, y + 1 is even, so
f(y + 1) = (y + 1) – 1 = y
When y is even, y – 1 is odd, so
f(y – 1) = (y – 1) + 1 = y
⇒ f : N → N is onto.
Hence, f is both one-one and onto.
Question. Let f : N → N be defined by

Find whether the function f is bijective
Answer.

Question. If f , g : R ® R be defined by f (x) = 2x + 1 and g(x) = x2 – , ∀ x ∈ R 2 , respectively. Then, find gof .
• Thinking Process
If f , g :R → R be two functions, then gof(x) =g { f(x)},∀ x ∈ R.
Answer. Given that, f(x) = 2x + 1 and g(x) = x2 – 2, ∀ x ∈ R.
∴ gof = g{f(x)}
= g(2x + 1)= (2 + 1)2 – 2
= 4x2 + 4x + 1 – 2
= 4x2 + 4x – 1
Question. Let f :R → R be the function defined by f (x) = 2x -3, ∀ x ∈ R. Write f-1.
Answer.

Question. If A = {a, b, c, d} and the function f = {(a, b), (b, d), (c, a), (d, c)}, write f-1.
Answer. Given that, A = {a, b, c, d}
and f = {(a, b), (b, d), (c, a), (d, c)}
f-1 = {(b,a), (d,b), (a,c), (c,d)}
Question. If f : R ® R is defined by f (x) = x2 – 3x + 2, write f { f (x)}.
• Thinking Process
To solve this problem use the formula i.e., (a + b + c)2 =(a2 + b2 + c2 + ab + bc + ca)
Answer.

Long Answer Type Questions
Question. Functions f , g : R ® R are defined, respectively, by f (x) = x2 + 3x + 1, g(x) = 2x – 3, find
(i) fog (ii) gof (iii) fof (iv) gog
Answer. Given that, f(x) = x 2 + 3x + 1, g(x) = 2x – 3

Question. Let A = R – {3}, B = R -{1}. If f : A → B be defined by
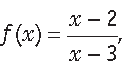
∀ x Î A. Then, show that f is bijective.
• Thinking Process
A function f : x → y is said to be bijective, if f is both one-one and onto.
Answer.

Question. Given, A = {2, 3, 4}, B = {2, 5, 6, 7}. Construct an example of each of the following
(i) an injective mapping from A to B.
(ii) a mapping from A to B which is not injective.
(iii) a mapping from B to A.
Answer. Given that, A = {2, 3, 4}, B = {2, 5, 6, 7}
(i) Let f : A → B denote a mapping
f = {(x, y) : y = x + 3}
i.e., f = {(2, 5), (3, – 6), (4, 7)}, which is an injective mapping.
(ii) Let g : A → B denote a mapping such that g = {(2, 2), (3, 5), (4, 5)}, which is not an injective mapping.
(iii) Let h : B → A denote a mapping such that h = {(2, 2), (5, 3), (6, 4), (7, 4)}, which is a mapping from B to A
Question. Let A = {1, 2, 3,K, 9} and R be the relation in A ´ A defined by (a, b) R (c, d) if a + d = b + c for (a, b), (c, d) in A ´ A. Prove that R is an equivalence relation and also obtain the equivalent class [(2, 5)].
Answer. Given that, A = {1, 2, 3,K, 9} and (a, b) R(c, d) if a + d = b + c for (a, b) ∈ A ´ A and
(c, d) ∈ A ´ A.
Let (a, b) R (a, b)
⇒ a + b = b + a, ” a, b ∈ A
which is true for any a, b ∈ A.
Hence, R is reflexive.
Let (a, b) R (c, d) a + d = b + c
c + b = d + a ⇒ (c, d) R (a, b)
So, R is symmetric.
Let (a, b) R (c, d) and (c, d) R (e, f )
a + d = b + c and c + f = d + e
a + d = b + c and d + e = c + f
(a + d) – (d + e) = (b + c) – (c + f )
(a – e) = b – f
a + f = b + e
(a, b) R (e, f )
So, R is transitive.
Hence, R is an equivalence relation.
Now, equivalence class containing [(2, 5)] is {(1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9)}.
Question. Let A =[- 1, 1], then, discuss whether the following functions defined
on A are one-one onto or bijective.
(i) f (x) = x/2
(ii) g(x) = |x|
(iii) h(x) = x|x|
(iv) k(x) = x2
Answer.


CASE STUDY 1:
A general election of Lok Sabha is a gigantic exercise. About 911 million people were eligible to vote and voter turnout was about 67%, the highest ever
ONE – NATION
ONE – ELECTION
FESTIVAL OF DEMOCRACY
GENERAL ELECTION – 2019
Let I be the set of all citizens of India who were eligible to exercise their voting right in general election held in 2019. A relation ‘R’ is defined on I as follows:
R = {(𝑉1,𝑉2)∶ 𝑉1,𝑉2 ∈𝐼 and both use their voting right in general election – 2019}
Question. Two neighbors X and Y∈ I. X exercised his voting right while Y did not cast her vote in general election – 2019. Which of the following is true?
a. (X,Y) ∈R
b. (Y,X) ∈R
c. (X,X) ∉R
d. (X,Y) ∉R
Answer
D
Question. Mr.’𝑋’ and his wife ‘𝑊’both exercised their voting right in general election -2019, Which of the following is true?
a. both (X,W) and (W,X) ∈ R
b. (X,W) ∈ R but (W,X) ∉ R
c. both (X,W) and (W,X) ∉ R
d. (W,X) ∈ R but (X,W) ∉ R
Answer
A
Question. Three friends F1, F2 and F3 exercised their voting right in general election-2019, then which of the following is true?
a. (F1,F2 ) ∈R, (F2,F3) ∈ R and (F1,F3) ∈ R
b. (F1,F2 ) ∈ R, (F2,F3) ∈ R and (F1,F3) ∉ R
c. (F1,F2 ) ∈ R, (F2,F2) ∈R but (F3,F3) ∉ R
d. (F1,F2 ) ∉ R, (F2,F3) ∉ R and (F1,F3) ∉ R
Answer
A
Question. The above defined relation R is __________
a. Symmetric and transitive but not reflexive
b. Universal relation
c. Equivalence relation
d. Reflexive but not symmetric and transitive
Answer
C
Question. Mr. Shyam exercised his voting right in General Election – 2019, then Mr. Shyam is related to which of the following?
a. All those eligible voters who cast their votes
b. Family members of Mr.Shyam
c. All citizens of India
d. Eligible voters of India
Answer
A
