Please refer to Probability Class 9 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 9 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 9 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 9.
Class 9 Mathematics Important Questions Probability
Very Short Answer Type Questions:
Question. In a game, a woman wins 16 times out of 20 balls she plays. Find the probability that she does not win the game.
Ans. P(woman wins the game) = 16/20 = 4/5
P(woman does not win the game) = 1 − 4/5 = 1/5
Question. A coin is tossed 500 times with the following frequencies : Head : 255, Tail : 245.
Then find the sum of the probabilities of each event.
Ans. P(Head appears) = 255/500 = 51/100
P(Tail appears) = 245/500 = 49/100
Sum of the probabilities = 51/100 +49/100 = 100/100 =1
Question. Ram and Priya are playing a game. Ram’s winning probability is 1/3 . Find the Priya’s winning probability.
Ans. Ram’s winning probability = 1/3
⇒ Priya’s winning probability = 1 − 1/3 = 2/3
Question. Find the probability of choosing a vowel randomly from the letters of the word ‘EXAMINATION’.
Ans. Number of letters in the word ′EXAMINATION′ = 11
Number of vowels in the word = 6
Required probability = 6/11
Question. A bag contains 6 green and 5 blue balls. If probability of choosing a green ball randomly is n/11
, then find the value of n.
Ans. Number of balls = 6 + 5 = 11 = n(S)
Let E be the event of choosing a green ball randomly.
∴ P(E)= n(E)/n(S) = 6/11 = n/11 ⇒ n=6
Short Answer Type Questions:
Question. A survey of 700 families was conducted to know their opinion about a particular newspaper. If 325 families liked that newspaper and the remaining families disliked it, find the probability that a family chosen at random
(i) likes the newspaper.
(ii) does not like it.
Ans. Total number of families = 700
Number of families who likes newspaper = 325
(i) P(a family chosen at random likes the newspaper) = 325/700 = = 13/28
(ii) P(a familty does not like the newspaper)
= 1 – P(a family likes the newspaper) = 1 – 13/28 = 15/28
Question. On one page of a telephone directory, there were 250 telephone numbers. The frequency distribution of their unit’s place digit (e.g., in the number 35285976, the unit’s place digit is 6) is given in the following table

Of these numbers, one number is chosen at random. What is the probability that
(i) The digit at its unit’s place is 8?
(ii) The digit at the unit place is not 7?
Ans. Total number telephone numbers on one page of a directory = 250
(i) Number of telephone numbers having 8 at its unit’s place = 31
∴ P(a number having 8 at its unit’s place) = 31/250.
(ii) Number of telephone numbers having 7 at its unit’s place = 27
∴ Number of telephone numbers not having 7 at its unit’s place = 250 – 27 = 223
∴ Required probability = 223/250.
Question. The diameters of circles (in mm) drawn in a design are given below.

If a circle is chosen at random, find the probability that
(i) chosen circle has diameter less than 28.
(ii) chosen circle has radius lying between 14 to 17.
(iii) chosen circle has diameter above 50.
Ans. Total number of circles = 34
(i) Let E be the event that chosen circle has diameter less than 28.
∴ n(E) = 3 + 5 = 8
∴ P(E)= n(E)/n(S) = 8/34 = 4/17
(ii) Let F be the event that chosen circle has radius lying between 14 to 17 i.e., has diameter between 28 to 34.
⇒ n(F) = 8
∴ P(F)= n(F)/n(S) = 8/34 = 4/17
(iii) Let G be the event that chosen circle has diameter above 50.
n(G) = 0
∴ P(G)= n(G)/n(S) = 0/34 = 0
Question. The record of a weather station shows that out of the past 365 consecutive days, its weather forecasts were correct 190 times.
(i) What is the probability that on a given day it was correct?
(ii) What is the probability that it was not correct on a given day?
Ans. Total number of days for which weather record available = 365
Number of days for which weather forecast was correct = 190
(i) P(the weather forecast was correct on a given day) = 190/365 = 38/73
(ii) P(the weather forecast was not correct on a given day) = 1 – 38/73 = 35/73
Question. The percentage of marks obtained by a student in monthly unit test are given below.

Find the probability that the student gets
(i) more than 80% marks.
(ii) atleast 60% marks.
Ans. Number of unit tests = 5
(i) Number of test in which student scored more than 80% marks = 1
∴ P(student gets more than 80% marks) = 1/5
(ii) Number of tests in which student scored atleast 60% marks = 4 (i.e., unit test II, III, IV and V)
∴ P(student gets atleast 60% marks) = 4/5
Question. A Tyre manufacturing company kept a record of the distances covered, before a tyre needed to be replaced. The table shows the result of 2000 cases:

If Anuj buy a tyre of this company, then what is the probability that
(i) It will need to be replaced before it has covered 3000 km?
(ii) It will last more than 6000 km?
(iii) It will need to be replaced after it has covers somewhere between 3000 km and 9000 km?
Ans. (i) The total number of cases = 2000
The frequency of a tyre that needs to be replaced before it covers 3000 km is 40.
∴ Probability (a tyre need to be replaced before it covers 3000 km) = 40/2000 = 0.02
(ii) The frequency of a tyre that last more than 6000 km
= 420 + 650 = 1070.
∴ Probability (a tyre will last more than 6000 km) = 1070/2000 = 0.535
(iii) The frequency of a tyre that requires replacement after covering somewhere between 3000 km and 9000 km = 890 + 420 = 1310.
∴ Probability (a tyre requires replacement after covering somewhere between 3000 km and 9000 km)
= 1310/2000 = 0.655
Question. A spinner is coloured by 3 different colours : yellow, blue and red in 12 equal sectors. After spinning the wheel, what is the probability that
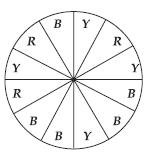
(i) wheel stops at yellow colour?
(ii) wheel stops at red colour?
(iii) wheel stops at blue colour?
Ans. (i) P(wheel stops at yellow colour) = 4/12 = 1/3
(ii) P (wheel stops at red colour) = 3/12 = 1/4
(iii) P (wheel stops at blue colour) = 5/12
Question. A letter is chosen at random from the letters of the word ′PROBABILITY′. Find the probability that the letter chosen is a
(i) consonant
(ii) vowel.
Ans. There are 11 letters in the word ‘PROBABILITY’.
(i) Let E be the event that the chosen letter is a consonant.
∴ n(E) = 7
∴ P(E)= n(E)/n(S) = 7/11
(ii) P(chosen letter is a vowel) = 1 – P(E)
= 1 − 7/11 = 4/11
Question. Two coins tossed simultaneously 1000 times with the following frequencies of different outcomes :
Two Heads : 320 times
One Head : 450 times
No Head : 230 times
Find the probability of occurrence of each of these events.
Ans. Let, the event of getting two heads be denoted by A,
event of getting one head be denoted by B, and event of getting no head be denoted by C.
Total number of trials = 1000
Number of trials in which, event A happens = 320
Number of trials in which, event B happens = 450
Number of trials in which, event C happens = 230
∴ P(A) = 320/1000 = 0.32 ; P(B) = 450/1000 = 0.45 ;
P(C) = 230/1000 = 0.23
Question. Here is an extract from a mortality table.
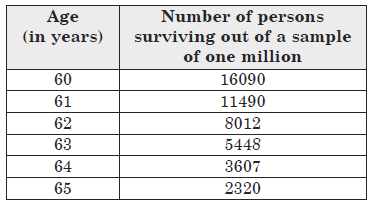
Based on this information, answer the following questions.
(i) What is the probability of a person ‘aged 60’ dying within a year?
(ii) What is the probability that a person ‘aged 61’ will live for 4 years?
Ans. (i) Number of persons aged 60 years = 16090
Number of persons aged 61 years = 11490
∴ Number of persons died before reaching their 61st birthday = 16090 – 11490 = 4600
So, P(a person aged 60 dying within a year) = 4600/16090 = 460/1609
(ii) Number of persons aged 61 years = 11490
Number of persons aged (61 + 4 = 65) years = 2320
∴ Number of persons who live for 4 years = 2320
So, P(a person aged 61 will live for 4 years) = 2320/11490 = 232/1149
Long Answer Type Questions:
Question. A inverter battery manufacturing company kept a record of battery life before it was replaced.

If you buy a battery of this company, then what
is the probability that
(i) it will need a replacement before 30 months?
(ii) it will last more than 42 months?
(iii) it will need to be replaced between 18 to 54 months?
(iv) it will need to be replaced after 54 months?
Ans. Total number of batteries = 800
(i) Number of batteries having life less than 30 months
= 200 + 80 = 280
∴ P(that the battery need replacement before 30 months)
= 280/800 = 7/20
(ii) Number of batteries having life more than 42 months
= 150 + 250 = 400
∴ P(that the battery last more than 42 months) = 400/800 = 1/2
(iii) Number of batteries having life between 18 to 54 months = 200 + 120 + 150 = 470
∴ P(that a battery need replacement between 18 to 54 months) = 470/800 = 47/80
(iv) Number of batteries having life more than 54 months = 250
∴ P(that a battery need replacement after 54 months) = = 250/800 = 5/16
Question. The following table gives the lifetime (in hours) of 400 CFL:
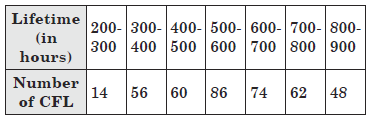
A CFL is selected at random. Find the probability that lifetime of the selected CFL is
(i) less than 400 hours
(ii) between 300 to 800 hours
(iii) atleast 700 hours
(iv) more than 800 hours
Ans. Total number of CFL = 400
(i) Number of CFL having lifetime less than 400 hours
= 14 + 56 = 70
∴ Probability that lifetime of the selected CFL is less than 400 hours = 70/400 = 7/40
(ii) Number of CFL having lifetime between 300 to 800
hours = 56 + 60 + 86 + 74 + 62 = 338
∴ Probability that lifetime of the selected CFL is
between 300 to 800 hours = 338/400 = 169/200
(iii) Number of CFL having lifetime atleast 700 hours
= 62 + 48 = 110
∴ Probability that lifetime of the selected CFL is atleast
700 hours = 110/400 = 11/40
(iv) Number of CFL having lifetime more than 800 hours = 48
∴ Probability that lifetime of the selected CFL is more than 800 hours = 48/400 = 3/25
Question. On a busy road, following data was observed about cars passing through it and number of occupants.

If a car passes by, then find the probability that it has
(i) exactly 5 occupants
(ii) more than 2 occupants
(iii) less than 5 occupants
(iv) atleast 4 occupants
Ans. Total number of cars observed = 142
(i) Number of cars having exactly 5 occupants = 15
∴ P(that a car has 5 occupants) = 15/142
(ii) Number of cars having more than 2 occupants
= 33 + 27 + 15 + 10 = 85
∴ P(that a car has more than 2 occupants) = 85/142
(iii) Number of cars having less than 5 occupants
= 29 + 28 + 33 + 27 = 117
∴ P(that a car has less than 5 occupants) = 117/142
(iv) Number of cars having atleast 4 occupants
= 27 + 15 + 10 = 52
∴ P(that a car has atleast 4 occupants) = 52/142 = 26/71

