Please refer to MCQ Questions Chapter 9 Differential Equations Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 9 Differential Equations in Class 12 Mathematics provided below to get more marks in exams.
Chapter 9 Differential Equations MCQ Questions
Please refer to the following Chapter 9 Differential Equations MCQ Questions Class 12 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 9 Differential Equations Class 12 Mathematics
Question. If f (x) = xn , then the value of
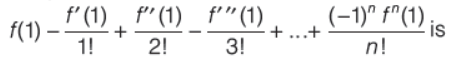
(a) 2n
(b) 0
(c) 2n-1
(d) None of these
Answer
B
Question. If f(x) = x2-x/x2+2x , where x ≠ 0, -2, then d/dx [f-1(x)] (whenever it is defined) is equal to
(a) -1/(1-x)2
(b) 3/(1-x)2
(c) 1/(1-x)2
(d) -3/(1-x)2
Answer
B
Question. Which of the following statements is/are true?
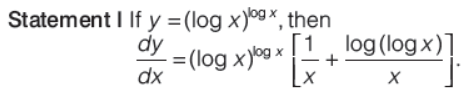
Statement II If y = cos(a cos x + b sin x ) for some constants a and b, then y’ = (a sin x – b cos x ) sin(a cos x + b sin x )
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
C
Question. Let f (x ) be a polynomial function of second degree. If f (1) = f (-1) and a,b,c are in AP, then f ¢ (a), f ‘ (b) and f ‘ (c) are in.
(a) AP
(b) GP
(c) Arithmetic-Geometric progression
(d) None of the above
Answer
A
Question. If f (x ) = cos x . cos2x . cos 4x . cos 8x × cos16x, then f'(π/4) is equal to
(a) √2
(b) 1/√2
(c) 1
(d) √3/2
Answer
A
Question. If sin y = x sin(a + y ), then dy/dx is equal to
(a) sin a/sin2(a+y)
(b) sin2(a+y)/sin a
(c) sin a sin2 (a + y)
(d) sin2 (a – y)/sin a
Answer
B
Question. If y = (1-x)(1+x2)(1+x4)……(1+x2n) , then dy/dx at x = 0 is equal to
(a) -1
(b) 1/(1+x2)
(c) x/(1+x2)
(d) x/(1-x2)
Answer
A
Question. If f(x) = | cos x|, then f’ (3π/4) is equal to
(a) 1/√2
(b) √2
(c) 1/2
(d) 2 √2
Answer
A
Question. If f : (-1,1)→ R be a differentiable function with f (0) =1 and f ‘ (0) =1. Let g (x ) = [f (2f (x ) + 2 )]2. The, g’ (0) is equal to
(a) 4
(b) -4
(c) 0
(d) -2
Answer
B
Question. If y = a cos-1x/1+a cos-1 and z = acos-1x , then dy/dz is equal to

Answer
C
Question. If y = f (x ) is an odd differentiable function defined on (- ∞, ∞) such that f ‘ (3) = – 2, then f ‘ (- 3) is equal to
(a) 4
(b) 2
(c) -2
(d) 0
Answer
C
Question. If f (x ) = 2+| x|-| x -1|-| x +1| , then
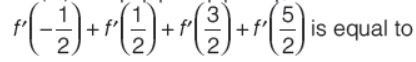
(a) 1
(b) -1
(c) 2
(d) -2
Answer
D
Question. If f and g are differentiable function satisfying g¢ (a) = 2,g(a) = b and fog = I (identity function). Then, f ‘ (b) is equal to
(a) 1/2
(b) 2
(c) 2/3
(d) None of these
Answer
A
Question. If graph of y = f (x ) is symmetrical about the Y-axis and that of y = g(x ) is symmetrical about the origin and if h(x ) = f (x ) ×g(x ), then d2h(x)/dx2 at x = 0 is
(a) f (0)g(0)
(b) 0
(c) can’t be determined
(d) None of the above
Answer
B
Question. If
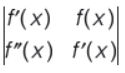
= 0,where f (x ) is continuously differentiable function with f ‘(x ) ¹ 0 and satisfies f (0) =1 and f ‘(0) = 2,
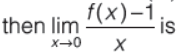
(a) 1
(b) 2
(c) 1/2
(d) 0
Answer
B
Question. If y = sec(tan-1 x) , then dy/dx at x =1 is equal to
(a) 1/√2
(b) 1/2
(c) 1
(d) √2
Answer
A
Question. If y is an implicit function of x defined by x2x – 2xx cot y – 1 = 0 Then, y ‘ (1) is equal to
(a) – 1
(b) 1
(c) log 2
(d) – log 2
Answer
A
Question. If f (x) = | x-1 | and g(x ) = f [f {f (x )}], then for x > 2, g’ (x ) is equal to
(a) – 1, if 2 ≤ x < 3
(b) 1, if 2 ≤ x < 3
(c) 1, if x > 2
(d) None of these
Answer
A
Question. If x = 2t/1+t2 and y = 1-t2/1+t2 , then dy/dx is equal to
(a) 2t/t2+1
(b) 2t/t2-1
(c) 2t/1-t2
(d) None of these
Answer
B
Question. For a > 0 ,t ∈ (0,π/2) , let x = √a sin-1 t and y = √a cos-1 t.
Then,1 +(dy/dx)2 equals
(a) x2/y2
(b) y2/x2
(c) x2+y2/y2
(d) x2+y2/x2
Answer
D
Question. If f(x) = |loge|x|, then f'(x) equals
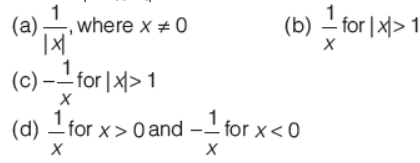
Answer
B
Question. For x ∈ (0,1/4) , if the derivative of tan-1(6x√x/1-9×3) is
√x . g(x ), then g(x ) equals
(a) 9/1+9x3
(b) 3x√x/1-9x3
(c) 3x/1-9x3
(d) 3/1+9x3
Answer
A
Question. Statement I If u = f (tan x ),v = g(sec x ) and f’ (1) = 2, g'(√2) = 4 , then (du/dv) x=π/4 = 1/√2
Statement II If u = f (x ),v = g(x ), then the derivative of f with respect to g is (du/dv) = du/dx/dv/dx .
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) Statement I is true; Statement II is false
(d)Statement I is false; Statement II is true
Answer
A
Question. If y = tan-1
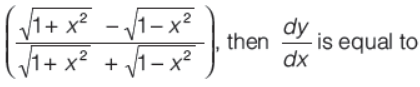
(a) x/√1-x4
(b) -x/√1-x2
(c) 2x/√1-x4
(d) None of these
Answer
A
Question. The derivative of y = (1 – x )(2 – x )K(n – x ) at x =1 is
(a) 0
(b) (-1)(n – 1)!
(c) n! – 1
(d) (-1)n-1(n-1)!
Answer
B
Question. Integrating factor of the differential equation dy/dx + y tan x – sec x = 0 is
(a) cos x
(b) sec x
(c) ecos x
(d) esec x
Answer
B
Question. In a culture the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000 if the rate of growth of bacteria is proportional to the number present.
(a) 2/log 11/10
(b) 2 log2/log (11/10)
(c) log 2/log 11
(d) log 2/log(11/10)
Answer
B
Question. The equation of the curve passing through the point (0 , π/4) whose differential equation is sin x cos y dx + cos x sin y dy = 0, is
(a) sec x sec y = √2
(b) cos x cos y = √2
(c) sec x = √2 cos y
(d) cos y = √2 sec y
Answer
A
Question. The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20, 000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009?
(a) 3125
(b) 31250
(c) 21350
(d) 12350
Answer
B
Question. Solution of the differential equation dx/dy – x log x/1+log x = ey/1+log x , if y(1) = 0, is
(a) xx = eyey
(b) ey = xey
(c) xx = yey
(d) None of these
Answer
A
Question. If the solution of the differential equation dy/dx = ax+3/2y+f represents a circle, then the value of ‘a’ is
(a) 2
(b) – 2
(c) 3
(d) – 4
Answer
B
Question. At any point (x, y) of a curve, the slope of tangent is twice the slope of the line segment joining the point of contact to the point (–4, –3). The equation of the curve given that it passes through (–2, 1) is
(a) x + 4 = (y + 3)2
(b) (x + 4)2 = (y – 3)
(c) x – 4 = (y – 3)2
(d) (x + 4)2 = |y + 3|
Answer
D
Question. If the slope of the tangent to the curve at any point P(x, y) is y/x – cos2 y/x , then the equation of a curve passing through (1 , π/4) is
(a) tan (y/x) + log x = 1
(b) tan (y/x) + log y = 1
(c) tan (x/y) + log x = 1
(d) tan (x/y)+ log y = 1
Answer
A
Question. The general solution of the differential equation (tan–1 y – x) dy = (1 + y2) dx is
(a) x = (tan–1 y + 1) + Ce – tan-1 y
(b) x = (tan–1 y – 1) + Ce – tan-1 y
(c) x = (tan–1 x – 1) + Ce – tan-1 x
(d) x = (tan–1 x + 1) + Ce – tan-1 x
Answer
B
Question. If x dy/dx = y (log y – log x + 1), then the solution of the equation is
(a) y log (x/y) = cx
(b) x log (y/x) = cy
(c) log (y/x) = cx
(d) log (x/y) = cy
Answer
C
Assertion and Reason type Questions :
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Assertion: x sin x dy/dx + (x + x cos x + sin x) y
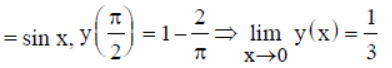
Reason: The differential equation is linear with integrating factor x(1 – cos x).
Answer
A
Question. Assertion: The differential equation x2 = y2 + xy dy/dx is an ordinary differential equation.
Reason: An ordinary differential equation involves derivatives of the dependent variable with respect to only one dependent variable.
Answer
A
Question. Let a solution y = y(x) of the differential equation x√x2-1 dy-y√y2-1 dx = 0 satisfy y(2) = 2/√3.
Assertion: y(x) sec (sec-1 x-π/6)
Reason: y(x) is given by 1/y = 2/√3/x – √1 – 1/x2
Answer
C
Question. For the differential equation d2y/dx2 + y = 0 , let its solution be y = φ1 (x) = 2 sin (x+π/4) .
Assertion: The function y = φ1(x) is called the particular solution.
Reason: The solution which is free from arbitrary constant, is called a particular solution.
Answer
A
Question. Assertion : dy/dx = x3-xy2+y3/x2y-x3 is a homogeneous differential equation.
Reason: The function F(x,y) = x3-xy2+y3/x2y-x3 is homogeneous.
Answer
A
Question. Let ƒ be a differentiable function such that ƒ'(x) = 7 − 3/4(ƒ(x))/x, (x>0) and ƒ(1) ≠ 4. Then (image 67)
(a) exists and equals 4/7 .
(b) exists and equals 4.
(c) does not exist.
(d) exists and equals 0.
Answer
B
Question. If y = y(x) is the solution of the differential equation, x(dy/dx) + 2y = x2 satisfying y(1) = 1, then y(1/2) is equal to:
(a) 7/64
(b) 1/4
(c) 49/16
(d) 13/16
Answer
C
Question. Let the population of rabbits surviving at time t be governed by the differential equation dp(t)/dt = (1/2)p(t) – 200. If p(0) = 100, then p(t) equals:
(a) 600 − 500 et/2
(b) 400 − 300 e−t/2
(c) 400 − 300 et/2
(d) 300 − 200 e−t/2
Answer
C
Question. If the general solution of the differential equation (image 42) for some function Φ, is given by y ln |cx| = x, where c is an arbitrary constant, then Φ(2) is equal to:
(a) 4
(b) 1/4
(c) – 4
(d) – 1/4
Answer
D
Question.Statement 1: The degrees of the differential equations dy/dx + y2 = x and d2y/dx2 + y = sin x are equal.
Statement 2: The degree of a differential equation, when it is a polynomial equation in derivatives, is the highest positive integral power of the highest order derivative involved in the differential equation, otherwise degree is not defined.
(a) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation of Statement 1.
(b) Statement 1 is false, Statement 2 is true.
(c) Statement 1 is true, Statement 2 is false.
(d) Statement 1 is true, Statement 2 is true; Statement 2 is a correct explanation of Statement 1.
Answer
D
Question. The differential equation of all circles passing through the origin and having their centres on the x-axis is
(a) y2 = x2 + 2xy(dy/dx)
(b) y2 = x2 – 2xy(dy/dx)
(c) x2 = y2 + xy(dy/dx)
(d) x2 = y2 + 3xy(dy/dx)
Answer
A
Question. The differential equation for the family of circle x2 + y2 – 2ay = 0, where a is an arbitrary constant is
(a) (x2 + y2)y’ = 2xy
(b) 2(x2 + y2) y’ = xy
(c) (x2 – y2)y’ = 2xy
(d) 2(x2 – y2) y’ = xy
Answer
C
Question. The general solution of the differential equation √(1+x2+y2+x2y2) + xy(dy/dx) = 0 is :
(where C is a constant of integration)
(image)
Answer
A
Question. The solution of the differential equation
(image 17)
(where C is a constant of integration)
(image 17)
Answer
A
Question. The equation of the curve passing through the origin and satisfying the differential equation (1+x2) dy/dx + 2xy = 4x2 is
(a) (1 + x2) y = x3
(b) 3(1 + x2) y = 2x3
(c) (1 + x2) y = 3x3
(d) 3(1 + x2) y = 4x3
Answer
D
Question. The integrating factor of the differential equation (x2 − 1) dy/dx + 2xy = x is
(a) 1/(x2 – 1)
(b) x2 – 1
(c) (x2 – 1)/x
(d) x/(x2 – 1)
Answer
B
Question. Let ƒ : (0, ∞)→(0, ∞) be a differentiable function such that ƒ(1) = e and (image 18) If ƒ(x) = 1, then x is equal to :
(a) 1/e
(b) 2e
(c) 1/2e
(d) e
Answer
A
Question. If f(x) is a differentiable function in the interval ( (0,∞) such that f(a) = 1 and (image 38) for each x > 0, then f(3/2) is equal to :
(a) 23/18
(b) 13/6
(c) 25/9
(d) 31/18
Answer
D
Question. The solution of the differential equation ydx – (x + 2y2)dy = 0 is x = f(y). If f(–1) = 1, then f(a) is equal to :
(a) 4
(b) 3
(c) 1
(d) 2
Answer
B
Question. The solution curve of the differential equation, (1+e−x)(1+y2)dy/dx = y2 , which passes through the point (0, 1), is :
(image 19)
Answer
C
Question. If x3 dy + xy dx = x2dy + 2y dx; y(2) = e and x > 1, then y(4) is equal to :
(a) 3/2 + √e
(b) (3/2)√e
(c) 1/2 + √e
(d) √e/2
Answer
B
Question. Let y – y(x) be the solution of the differential equation sin x(dy/dx) + y cos x = 4x, x ∈ (0, π). If y(π/2) = 0, then y(π/6) is equal to :
(a) (−8/9√3)π2
(b) − (8/9)π2
(c) − (4/9)π2
(d) (4/9√3)π2
Answer
B
Question. Let y = y(x) be the solution of the differential equation dy/dx + 2y = ƒ(x), where (image 70) If y (0) = 0, then y(3/2) is
(a) (e2−1)/2e3
(b) (e2−1)/e3
(c) 1/2e
(d) (e2+1)/2e4
Answer
A
Question. If f2(x) = tan–1 (sec x + tan x), –(π/2) < x < (π/2), and f(0) = 0, then f(1) is equal to:
(a) (π+1)/4
(b) 1/4
(c) (π−1)/4
(d) (π+2)/4
Answer
A
Question. The differential equation of the family of curves, x2 = 4b (y + b), b ∈ R, is:
(a) x(y’)2 = x + 2yy’
(b) x(y’)2 = 2yy’ – x
(c) xy² = y’
(d) x(y’)2 = x – 2yy’
Answer
A
Question. The differential equation representing the family of ellipse having foci either on the x-axis or on the y-axis centre at the origin and passing through the point (0, 3) is:
(a) xyy’ + y2 – 9 = 0
(b) x + yy” = 0
(c) xyy” + x (y’)2 – yy’ = 0
(d) xyy’ – y2 + 9 = 0
Answer
C
Question. Let y = y(x) be a solution of the differential equation, (image 26) If y(1/2) = √3/2, then y(−1/√2) is equal to:
(a) √3/2
(b) – 1/√2
(c) 1/√2
(d) – √3/2
Answer
C
Question. If cos x(dy/dx) − y sin x = 6x, (0 < x < π/2) and y(π/3) = 0, then y(π/6) is equal to:
(a) π2/2√3
(b) – π2/2
(c) – π2/2√3
(d) – π2/4√3
Answer
C
Question. Given that the slope of the tangent to a curve y = y(x) at any point (x, y) is 2y/x2 . If the curve passes through the centre of the circle x2 + y2 – 2x – 2y = 0, then its equation is:
(a) x loge| y | = 2(x – 1)
(b) x loge | y | = – 2(x – 1)
(c) x2 loge | y | = – 2(x – 1)
(d) x loge | y | = x – 1
Answer
A
Question. If y = ((2/π)x − 1) cosec x is the solution of the differential equation, dy/dx + p(x)y = 2/π cosec x, 0 < x < π/2, then the function p(x) is equal to:
(a) cot x
(b) cosec x
(c) sec x
(d) tan x
Answer
A
Question. The normal to a curve at P(x, y) meets the x-axis at G. If the distance of G from the origin is twice the abscissa of P, then the curve is a
(a) circle
(b) hyperbola
(c) ellipse
(d) parabola
Answer
B
Question. If x(dy/dx) = y (log y – log x + 1), then the solution of the equation is
(a) y log(x/y) = cx
(b) x log(y/x) = cy
(c) log(y/x) = cx
(d) log(x/y) = cy
Answer
C
Question. If y = y (x) is the solution of the differential equation (5 + ex)/(2+y) · dy/dx + ex = 0 satisfying y (0) = 1, then a value of y(loge 13) is :
(a) 1
(b) – 1
(c) 0
(d) 2
Answer
B
Question. The curve amongst the family of curves represented by the differential equation, (x2 – y2) dx + 2xydy = 0 which passes through (1, 1), is:
(a) a circle with centre on the x-axis.
(b) an ellipse with ma or axis along the y-axis.
(c) a circle with centre on the y-axis.
(d) a hyperbola with transverse axis along the x-axis.
Answer
A
Question. If y = y(x) is the solution of the differential equation dy/dx = (tan x – y)sec2x, x ∈ (- π/2, π/2), such that y (0) = 0, then y(- π/4) is equal to :
(a) e – 2
(b) 1/2 – e
(c) 2 + 1/e
(d) 1/e – 2
Answer
A
Question. Let y = y(x) be the solution of the differential equation, dy/dx + y tan x = 2x + x2tan x, x ∈ (– π/2, π/2), such that y(0) = 1. Then :
(image 61)
Answer
D
Question. Let f : [0, 1] → R be such that f(xy) = f(x).f(y), for all x, y ∈ [0, 1], and f(0) ≠ 0. If y = y(x) satisfies the differential equation, dy/dx = f(x) with y(0) = 1, then y(1/4) + y(3/4) is equal to:
(a) 3
(b) 4
(c) 2
(d) 5
Answer
A
Question. The curve satisfying the differential equation, (x2 – y2)dx + 2xydy = 0 and passing through the point (1, 1) is
(a) a circle of radius two
(b) a circle of radius one
(c) a hyprbola
(d) an ellipse
Answer
B
Question. Consider the differential equation y2dx + (x − 1/y)dy = 0. If y(1) = 1, then x is given by :
(image 79)
Answer
C
Question. Solution of the differential equation cos x dy = y(sin x − y)dx, 0 < x < π/2 is
(a) y sec x = tan x + c
(b) y tan x = sec x + c
(c) tan x = (sec x + c) y
(d) sec x = (tan x + c) y
Answer
D
Question. If (2 + sin x) dy/dx + (y + 1) cos x = 0 and y(0) = 1, then y(π/2) is equal to :
(a) 4/3
(b) 1/3
(c) − 2/3
(d) − 1/3
Answer
B
Question. The differential equation whose solution is Ax2 + By2 = 1 where A and B are arbitrary constants is of
(a) second order and second degree
(b) first order and second degree
(c) first order and first degree
(d) second order and first degree
Answer
D
Question. The differential equation representing the family of curves y2 = 2c ( x + √c) , where c > 0, is a parameter, is of order and degree as follows :
(a) order 1, degree 2
(b) order 1, degree 1
(c) order 1, degree 3
(d) order 2, degree 2
Answer
C
Question. If a curve y = f(x) passes through the point (1, –1) and satisfies the differential equation, y(1 + xy) dx = x dy, then f(− 1/2) is equal to :
(a) 2/5
(b) 4/5
(c) − 2/5
(d) − 4/5
Answer
B
We hope you liked the above-provided MCQ Questions Chapter 9 Differential Equations Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.


