Please refer to Conic Sections Class 11 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 11 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 11 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 11.
Class 11 Mathematics Important Questions Conic Sections
Question. The equation of the diameter of the circle x2 + y2 + 2x − 4y −11 = 0 which bisects the chords intercepted on the line 2x − y + 3 = 0 is:
(a) x + y − 7 = 0
(b) 2x − y − 5 = 0
(c) x + 2y − 3 = 0
(d) None of these
Answer
C
Question. The length of common chord of the circles (x−a)2 + y2 =a2 and x2 + ( y − b)2 = b2 is:
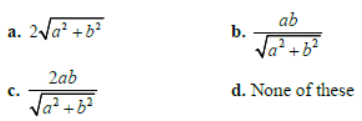
Answer
C
Question. The length of common chord of the circles x2 + y2 =12 and x2 + y2 − 4x + 3y − 2 = 0 , is:
(a) 4√2
(b) 5√2
(c) 2√2
(d) 6√2
Answer
A
Question. The equation of the circle having its centre on the line x + 2y − 3 = 0 and passing through the points of intersection of the circles x2 + y2 − 2x − 4y +1 = 0 and x2 + y2 − 4x − 2y + 4 = 0 , is:
(a) x2 + y2 −6x + 7 = 0
(b) x2 + y2 −3y + 4 = 0
(c) x2 + y2 −2x − 2y + 1 = 0
(d) x2 + y2 −2x − 4y + 4 = 0
Answer
A
Question. A line lx + my + n = 0 meets the circle x2 + y2 = a at the points P and Q. The tangents drawn at the points P and Q meet at R, then the coordinates of R is:
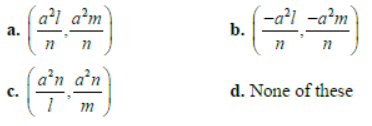
Answer
B
Question. Length of the common chord of the circles x2 + y2 + 5x + 7 y + 9 = 0 and x2 + y2 + 7x + 5y + 9 = 0 is:
(a) 9
(b) 8
(c) 7
(d) 6
Answer
D
Question. Which of the following is a point on the common chord of the circles x2 + y2 +2x−3y+6=0 and x2 + y2 +x−8y−13 =0?
(a) (1, –2)
(b) (1, 4)
(c) (1, 2)
(d) (1, –4)
Answer
D
Question. The equation of the chord of contact, if the tangents are drawn from the point (5, –3) to the circle x2 + y2 =10 , is:
(a) 5x − 3y =10
(b) 5x + 3y =10
(c) 3x + 5y =10
(d) 3x − 5y =10
Answer
A
Question. The equation of the circle having as a diameter, the chord x − y −1 = 0 of the circle 2x2 + 2y2 − 2x − 6y − 25 = 0 , is:
(a) x2 + y2 − 3x −y−29/2 = 0
(b) 2x2 + 2y2 + 2x −5y−29/2 = 0
(c) 2x2 + 2y2 − 6x −2y−21 = 0
(d) None of these
Answer
C
Question. A foot of the normal from the point (4, 3) to a circle is (2,1) and a diameter of the circle has the equation 2x – y = 2. Then the equation of the circle is:
(a) x2 + y2 + 2x −1 = 0
(b) x2 + y2 − 2x −1 = 0
(c) x2 + y2 − 2y −1 = 0
(d) None of these.
Answer
B
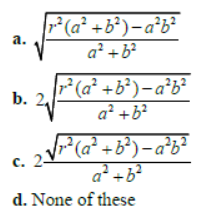
Answer
B
Question. From the origin chords are drawn to the circle (x−1)2 +y2 =1 The equation of the locus of the middle points of these chords is:
(a) x2 + y2 − 3x = 0
(b) x2 + y2 − 3y = 0
(c) x2 + y2 − x = 0
(d) x2 + y2 − y = 0
Answer
C
Question. The diameter of the circle x2 + y2 – 4x + 2y – 11 = 0 corresponding to a system of chords parallel to the line x – 2y + 1= 0?
(a) x − 2y + 3 = 0
(b) 2x − y + 3 = 0
(c) 2x + y − 3 = 0
(d) None of these
Answer
C
Question. The polar of the point (5 .–1/2) with respect to circle (x –2)2 + y2 = 4 is:
(a) 5x – 10y + 2 = 0
(b) 6x – y – 20 = 0
(c) 10x – y – 10 = 0
(d) x – 10y – 2 = 0
Answer
B
Question. The number of common tangents to the circles x2 + y2 =4 and x2 + y2 − 6x − 8y = 24 is:
(a) 0
(b) 1
(c) 3
(d) 4
Answer
B
Question. The pole of the straight line 9x + y − 28 = 0with respect to circle 2x2 + 2y2 − 3x + 5y − 7 = 0 , is:
(a) (3, 1)
(b) (1, 3)
(c) (3, –1)
(d) (–3, 1)
Answer
C
Question. There are two circles whose equations are x2 + y2 = 9 and x2 + y2 − 8x − 6y + n = 0, n∈Z. If the two circles have exactly two common tangents, then the number of possible values of n is:
(a) 2
(b) 7
(c) 9
(d) 6
Answer
C
Question. A circle passes through the origin and has its centre on y =x. If it cuts x + y − 4x − 6y +10 = 0 orthogonally, then the equation of the circle is:
(a) x2 + y2 − x − y = 0
(b) x2 + y2 − 6x − 4 y = 0
(c) x2 + y2 − 2x − 2 y = 0
(d) x2 + y2 + 2x + 2y = 0
Answer
C
Question. The equation of the circle, which passes through the point (2a, 0) and whose radical axis is x = a/2 with respect to the circle x2 + y2 = a2, will be:
(a) x2 + y2 – 2ax = 0
(b) x2 + y2 + 2ax = 0
(c) x2 + y2 + 2ay = 0
(d) x2 + y2 – 2ay = 0
Answer
A
Question. Circles x2 + y2 − 2x − 4y = 0 and x2 + y2 −8y − 4 = 0 ?
(a) Touch each other internally
(b) Touch each other externally
(c) Cuts each other at two points
(d) None of these
Answer
A
Question. The condition of the curves ax2 +by2 =1and a’ x2 + b’ y2 =1 to intersect each other orthogonally, is
(a) 1/a − 1/a’ = 1/a − 1/b’
(b) 1/a + 1/a’ = 1/a + 1/b’
(c) 1/a + 1/b = 1/a’+ 1/b’
(d) None of these
Answer
A
Question. The locus of the centres of the circles which touch externally the circles x2 + y2 =a and x2 + y2 = 4ax, will be:
(a) 12x2 − 4y2 − 24ax + 9a = 0
(b) 12x2 + 4y2 − 24ax + 9a = 0
(c) 12x2 − 4y2 + 24ax + 9a = 0
(d) 12x2 + 4y2 + 24ax + 9a = 0
Answer
A
Question. The equation of a circle passing through origin and coaxial to circles x2 + y2 = a2 and x2 + y2 + 2ax = 2a , is:
(a) x2 + y2 =1
(b) x2 + y2 + 2ax = 0
(c) x2 + y2 − 2ax = 0
(d) x2 + y2 = 2a2
Answer
C
Question. The equation of line passing through the points of intersection of the circles 3x2 + 3y2 − 2x +12y −9 = 0 and x2 + y2 + 6x + 2y −15 = 0 , is:
(a) 10 x − 3y − 18 = 0
(b) 10 x + 3y − 18 = 0
(c) 10 x + 3y + 18 = 0
(d) None of these
Answer
A
Question. If α is the angle subtended at P(x1,y1) by the circle S ≡ x2 + y2 +2gx+2 fy +c = 0, then

Answer
B,D
Question. The equation of circle which passes through the point (1,1) and intersect the given circles x2 + y2 + 2x + 4y + 6 = 0 and x2 + y2 + 4x + 6y + 2 = 0 orthogonally, is:
(a) x2 + y2 +16x +12y + 2 = 0
(b) x2 + y2 −16x −12y − 2 = 0
(c) x2 + y2 −16x +12y + 2 = 0
(d) None of these
Answer
C
Question. One of the limit point of the coaxial system of circles containing x2 + y2 − 6x − 6y + 4 = 0, x2 + y2 − 2x −4y + 3 = 0 is:
(a) (−1,1)
(b) (−1,2)
(c) (−2,1)
(d) (−2,2)
Answer
A
Question. The equations of the tangents drawn from the origin to the circle x2 + y2 + 2rx +2hy + h2 = 0, are:
(a) x = 0
(b) y = 0
(c) (h2 − r2 )x − 2rhy = 0
(d) (h2 − r2)x + 2rhy = 0
Answer
A,C
Question. The equation of a common tangent to the circle x2 + y2 +14x − 4y + 28 = 0 and x2 + y2 −14x+4y −28 = 0 is
(a) x − 7 = 0
(b) y − 7 = 0
(c) 28x + 45y + 371 = 0
(d) 7x − 2 y +14 = 0
Answer
B,C
Question. The equation of a circle passing through points of intersection of the circles 2x2 + y2 +13x − 3y = 0 and 2x2 + 2y2 + 4x − 7 y − 25 = 0 and point (1, 1) is:
(a) 4x2 + 4y2 − 30x −10y − 25 = 0
(b) 4x2 + 4y2 + 30x −13y − 25 = 0
(c) 4x2 + 4y2 −17x −10y + 25 = 0
(d) None of these
Answer
B
