Please refer to MCQ Questions Chapter 3 Trigonometric Functions Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 3 Trigonometric Functions in Class 11 Mathematics provided below to get more marks in exams.
Chapter 3 Trigonometric Functions MCQ Questions
Please refer to the following Chapter 3 Trigonometric Functions MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 3 Trigonometric Functions Class 11 Mathematics
Question. The value of tan 20° tan 40° tan 60° tan 80° is equal to
(a) 1
(b) 2
(c) 3
(d) √3/2
Answer
C
Question. The value of sin 36° sin 72° sin 108° sin 144° is equal to
(a) 1/4
(b) 1/16
(c) 3/4
(d) 5/16
Answer
D
Question. The value of 2 cos x – cos 3x – cos 5x is equal to
(a) 16cos3x sin2x
(b) 16sin3x cos2x
(c) 4cos3x sin2x
(d) 4sin3x cos2x
Answer
A
Question. The value of tan 75° – cot 75° is equal to
(a) 2√3
(b) 2 + √3
(c) 2 – √3
(d) 1
Answer
A
Question. In a ΔPQR, ∠R =π/2. If tan (p/2)3 and tan (Q/2) are the roots of ax2 + bx + c= 0, ¹ 0, then
(a) b = a + c
(b) b = c
(c) c = a + b
(d) a = b + c
Answer
C
Question. In a ΔABC, medians AD and BE are drawn. If AD = 4, ∠DAB = π/6 and ∠ABE = π/3, then the area of the ΔABC is
(a) 8 / 3 sq units
(b) 16 / 3 sq units
(c) 32 / 3 3 sq units
(d) 64 / 3 sq units
Answer
C
Question. Which of the following is correct ?
(a) sin 1° > sin 1
(b) sin 1° < sin 1
(c) sin 1° = sin 1
(d) sin 1 = sin π18° sin 1
Answer
B
Question. If sin (α + β) = 1, sin (α – β) = , 1/2 then tan (α + 2β) tan (2α + β) is equal to
(a) 1
(b) -1
(c) zero
(d) None of these
Answer
A
Question. In a ΔPQR, if 3 sin P + 4 cosQ = 6 and 4 sinQ + 3 cos P = 1, then the ∠R is equal to
(a) 5π/6
(b) π/6
(c) π/4
(d) 3π/4
Answer
B
Question. The equation esin x – e -sin x – 4 = 0 has
(a) infinite number of real roots
(b) no real roots
(c) exactly one real root
(d) exactly four real roots
Answer
B
Question. If y = sin + , 2 q cosec2 q q ¹ 0, then
(a) y = 0
(b) y ≤ 2
(c) y ³ – 2
(d) y > 2
Answer
D
Question. Consider the following statements :
I. If sin A = sin B, then we have sin 2A = sin 2B always.
II. The value of cosπ/7cos4π/7cos5π/7 is 1/4.
Which of the statements given above is/are correct ?
(a) Only (I)
(b) Only (II)
(c) Both (I) and (II)
(d) Neither (I) nor (II)
Answer
D
Question. If y = 1 + 4sin2x cos2x , then
(a) 1 ≤ y ≤ 2
(b) -1 ≤ y ≤ 1
(c) -3 ≤ y ≤ 3
(d) None of these
Answer
A
Question. The greatest and least value of sin x cos x are respectively
(a) 1, -1
(b) 1/2, -1/2
(c) 1/4 ,1/4
(d) 2, – 2
Answer
B
Question. cos2θ + 2cosθ is always
(a) greater than – 3/2
(b) less than or equal to 3/2
(c) greater than or equal to – 3/2 and less than or equal to 3
(d) None of the above
Answer
C
Question. The maximum value of (cosα1 ) (cosα2)…… (cosαn) = under the restriction 0 ≤ α,α…..,αn≤ π/2 and (cotα1 ) (cotα2 ) (cotαn ) = 1 is
(a) 1/2 n/2
(b)1/2n
(c) 1/2n
(d) 1
Answer
A
Question. The minimum value of 3cos x + 4sin x + 8 is
(a) 5
(b) 9
(c) 7
(d) 3
Answer
D
Question. Total number of solutions of cos x = √(1 – sin2x) in [0, 2π] is equal to
(a) 2
(b) 3
(c) 5
(d) None of these
Answer
A
Question. Total number of solutions of the equation 3x + tan x =5n/2 in x ∈ [0, 2n], is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. The number of values of x in the interval [0, 5n] satisfying the equation 3sin2x – sin x + 2 = is
(a) 0
(b) 5
(c) 6
(d) 10
Answer
C
Question. The number of solutions of the equation 1 + sinxsin2 x/2=in [- n, n] is
(a) zero
(b) one
(c) two
(d) three
Answer
A
Question. If cotθ + tanθ = 2 cosec q, then find the general value of q.
(a) 2nπ ± 1/4
(b) 2nπ ± π/4
(c) 2nπ ± π/3
(d) None of these
Answer
C
Question. The equation esin x – e-sin x – 4 = 0 has
(a) no solution
(b) two solutions
(c) three solutions
(d) None of these
Answer
A
Question. The number of solutions of the equation cos x = 2 [x], where [×] is the greatest integer, is
(a) one
(b) two
(c) infinite
(d) nil
Answer
D
Question. The number of ordered pairs (x, y) satisfying y = 2 sin x and y = 5x2 + 2x + 3 2 is
(a) 0
(b) 1
(c) 2
(d) ∞
Answer
A
Question. The most general solutions of the equation sec x – 1 = (√2 – 1) tan x are given by
(a) nπ + π/8
(b) 2nπ , 2nπ + π/4
(c) 2 nπ
(d) None of these
Answer
B
Question. If the equation cos3x + cos2x = sin 3x/2 + sin x/2
0 ≤ x ≤ 2p, then the number of values of x is
(a) 6
(b) 7
(c) 4
(d) 5
Answer
D
Question. If sec x cos 5x + 1 = 0, where0 < x < 2p, then x is equal to
(a) π/5 ,π/4
(b) π/5
(c) π/4
(d) None of these
Answer
C
Question. Total number of solutions of sin4 x + cos4 x + sinx cosx in [0, 2π] is equal to
(a) 2
(b) 4
(c) 6
(d) 8
Answer
A
Question. The general value of x for which cos2x ,1/2 and sin 2x are in AP, are given by
(a) nπ, nπ+π/2
(b) nπ, nπ+π/4
(c) nπ,+π/4 + 3π/4
(d) None of these
Answer
B
Question. The equationsin x + sin y + sin z = – 3 for0 ≤ x ≤ 2p,0 ≤ y ≤ 2p, 0 ≤ z ≤ 2π has
(a) one solution
(b) two sets of solutions
(c) four sets of solutions
(d) no solution
Answer
A
Question. The equation 2cos2 x/2 sin2x , = x2 + x2 , x< π/9 has
(a) no real solution
(b) one real solution
(c) more than one real solutions
(d) None of the above
Answer
A
Question. If tan a, tan b and tan g are the roots of the equation x2 – px2 – r = 0, then the value of (1 tan2α ) (1 tan2β ) (1 tan2γ ) is equal to
(a) (p – r )2
(b) 1 + (p – r )2
(c) 1 – (p – r )2
(d) None of these
Answer
B
Question. If a, b, g and d are four solutions of the equation tan (θ+π/4) 3tan 3θ, then tan α tan β tan ϒ tan d equals
(a) 3
(b) 1/3
(c) – 1/3
(d) None of these
Answer
C
Question. The least value of cosec2x + 25 sec2x is
(a) 0
(b) 26
(c) 28
(d) 36
Answer
D
Question. If tan a/2 and tan b/2 are the roots of the equation 8×2 – 26x + 15 = 0, then cos (a + b) is equal to
(a) – 627/725
(b) 627/725
(c) -1
(d) None of these
Answer
A
Question. The number of values of q in the interval (-π/2 , π/2) satisfying the equation (√3)sec2θ =tan4θ + 2tan2θ is
(a) 1
(b) 2
(c) 3
(d) None of these
Answer
B
Question. If sin4x + cos4y + 2 = 4 sinx cosy and 0 ≤x,y≤π/2 then sin x + cos y is equal to
(a) –2
(b) 0
(c) 2
(d) 3/2
Answer
C
Question. The equation cos4x – (λ+2)cos2-x (λ+3) = 0 possesses a solution, if
(a) λ > – 3
(b) λ < – 2
(c) -3 ≤ λ ≤- 2
(d) l is any positive integer
Answer
C
Question. The arithmetic mean of the roots of the equation 4cos3x – 4cos2x – cos (315π + x) in the interval (0, 315) is equal to
(a) 50π
(b) 51π
(c) 100π
(d) 315π
Answer
B
Question. Set a, b∈[-p, p] be such that cos (a – b) = 1 and cos (a+b) = 1/e . The number of pairs of aand b satisfying the above system of equations is
(a) 0
(b) 1
(c) 2
(d) 4
Answer
D
Question. The number of solutions of the equation x3+x2+4x+2 sin = 0 in 0 ≤ x ≤ 2π is
(a) zero
(b) one
(c) two
(d) four
Answer
B
Question. Let a and b be any two positive values of x for which 2 cos x,|cos x| and 1 3 – cos2 x are in GP. The minimum value of|a – b|is
(a) π/3
(b) π/4
(c) π/2
(d) None of these
Answer
D
Question. If tanθ = sinα – cosα/sinα + cosα , then
(a) sinα – cosα = ± 2 sinθ
(b) sinα + cosα = ± 2 cosθ
(c) cos2θ = sin 2α
(d) sin2θ + cos 2α = 0
Answer
(a,b,c,d)
Question. tan|x|=|tan x|, if
(a) x ∈{-π(2 k + 1)/2, – πk}, k ∈ I
(b) x ∈[πk, π(2 k + 1) / 2], k ∈ I
(c) x ∈{-πk, – π(2 k – 1) / 2}, k ∈ I
(d) x ∈{π(2 k – 1) / 2, πk}, k ∈ I
Answer
(a,b)
Question. The number of solutions of the equation 2cos (x/2) = 3x + 3-x is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. The number of real solutions of the equation sin (ex) x = 5x + 5-x is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. The expression tanA/1-cotA + cotA/1-tanA can be written as
(a) sin A cos A + 1
(b) sec A cosec A + 1
(c) tan A + cot A
(d) sec A + cosec A
Answer
B
Question. Let A and B denote the statements
A : cosα + cosβ + cosγ = 0
B: sinα + sinβ + sinγ = 0
If cos (β – γ) + cos (γ – α) + cos (α – β) = – , 3/2 then
(a) A is true and B is false
(b) A is false and B is true
(c) both A and B are true
(d) both A and B are false
Answer
C
Question. The number of values of x in [0, 3p] such that 2sinx + 5sin x – 3 = 0 is
(a) 1
(b) 2
(c) 4
(d) 6
Answer
C
Question. If sinx/cosx x secx/cosecx x tanx/cotx x = 9, where x ∈ (0, π/2) then the value of x is equal to
(a) π/4
(b) π/3
(c) π/2
(d) π
Answer
B
Question. Angle subtended at the centre by an arc of length 1 unit in a unit circle is said to have a measure of
(a) 1 degree
(b) 1 grade
(c) 1 radian
(d) 1 arc
Answer
C
Question. If x = sec θ + tan θ, then x + 1/x =
(a) 1
(b) 2 sec θ
(c) 2
(d) 2 tan θ
Answer
B
Question. If the arcs of the same lengths in two circles subtend angles 65° and 110° at the centre, the ratio of their radii is
(a) 12 : 13
(b) 22 : 31
(c) 22 : 13
(d) 21 : 13
Answer
C
Question. The value of sin 765° is 1/√n. Value of n is
(a) 2
(b) 3
(c) 4
(d) 0
Answer
A
Question. The length of an arc of a circle of radius 3 cm, if the angle subtended at the centre is 30° is (π = 3.14)
(a) 1.50 cm
(b) 1.35 cm
(c) 1.57 cm
(d) 1.20 cm
Answer
C
Question. If sin x + cos x = 1/5, then tan 2x is
(a) 25/17
(b) 7/25
(c) 25/7
(d) 24/7
Answer
D
Question. Value of √3 cosec 20° – sec 20° is
(a) 3
(b) 3/2
(c) 1
(d) 4
Answer
D
Question. The number of solution of tan x + sec x = 2cos x in (0, 2π) is
(a) 2
(b) 3
(c) 0
(d) 1
Answer
B
Question. The general solution of sin2 θ sec θ + √3 tan θ = 0 is
(a) θ = nπ + (–1)n+1 π/3, θ = nπ, n ∈ Z
(b) θ = nπ, n ∈ Z
(c) θ = nπ + (–1)n+1 π/3, n ∈ Z
(d) θ = nπ/2 , n ∈ Z
Answer
B
Question. If 2 cos2 x + 3 sin x – 3 = 0, 0 ≤ x ≤ 180°, then x =
(a) 30°, 90°, 150°
(b) 60°, 120°, 180°
(c) 0°, 30°, 150°
(d) 45°, 90°, 135°
Answer
A
Question. Match the following in column-I with the given in column-II.
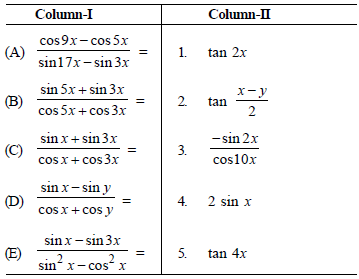
Codes:
A B C D E
(a) 3 5 2 1 4
(b) 3 5 1 4 2
(c) 3 1 2 5 4
(d) 3 5 1 2 4
Answer
D
Question. The radius of the circle in which a central angle of 60° intercepts an arc of length 37.4 cm is (Use π = 22/7)
(a) 37.5 cm
(b) 32.8 cm
(c) 35.7 cm
(d) 34.5 cm
Answer
C
Question. The value of tan 70° – tan 20° / tan 50° =
(a) 1
(b) 2
(c) 3
(d) 0
Answer
B
Question. The solution of the equation cos2θ + sinθ + 1 = 0, lies in the interval
(a) (–π/4,π/4)
(b) (π/4,3π/4)
(c) (3π/4,5π/4)
(d) (5π/4,7π/4)
Answer
D
Question. The number of solutions of the given equation tan θ + sec θ = √3, where 0 ≤ θ ≤ 2π is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
Question. The general solution of sin2 θ sec θ + √3 tan θ = 0 is
(a) θ = nπ + (–1)n + 1 π/3 , θ = nπ; n ∈ I
(b) θ = nπ; n ∈ I
(c) θ = nπ/2, n ∈ I
(d) θ = nπ/2 + (–1)n + 1 , π/2 ,θ = nπ; n ∈ I
Answer
B
Question. If tan (cot x) = cot (tan x), then
(a) sin 2x = 2/(2n+1)π
(b) sin x = 4/(2n+1)π
(c) sin 2x = 4/(2n+1)π
(d) None of these
Answer
C
Question.Match the following in column-I with the given in column-II.
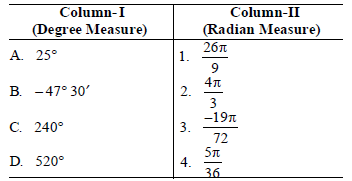
Codes:
A B C D
(a) 4 1 2 3
(b) 4 3 2 1
(c) 1 3 2 4
(d) 1 4 3 2
Answer
B
Question. If 12 cot2 θ – 31 cosec θ + 32 = 0, then the value of sin θ is
(a) 3/5 or 1
(b) 2/3 or –2/3
(c) 4/5 or 3/4
(d) ±1/2
Answer
C

We hope you liked the above provided MCQ Questions Chapter 3 Trigonometric Functions Class 11 Mathematics with solutions. If you have any questions please ask us in the comments box below.

