Please refer to MCQ Questions Chapter 15 Statistics Class 11 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 11 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 11 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 15 Statistics in Class 11 Mathematics provided below to get more marks in exams.
Chapter 15 Statistics MCQ Questions
Please refer to the following Chapter 15 Statistics MCQ Questions Class 11 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 15 Statistics Class 11 Mathematics
Question. The mean height of 25 male workers in a factory is 61 cm and the mean height of 35 female workers in the same factory is 58 cm. The combined mean height of 60 workers in the factory is
(a) 59.25
(b) 59.5
(c) 59.75
(d) 58.75
Answer
A
Question: The mean and standard deviation of some data for the time taken to complete a test are calculated with the following results Number of observations = 25, mean = 18.2 s, standard deviation = 3.25 s.
Further, another set of 15 observations x1,x2,…,x15, also in seconds, is now available and we have

=5524 Find the standard deviation based on all 40 observations.
(a) 3.80
(b) 3.87
(c) 3.70
(d) None of these
Answer
B
Question: If the variance of 1, 2, 3, 4, 5,…,10 is 99/12, then the standard deviation of 3, 6, 9, 12,…, 30 is
(a) 297/4
(b) 3/2√33
(c) 3/2√2
(d) √99/12
Answer
B
Question: If for a distribution ∑(x-5)=3, ∑(x-5)2 =43 and the total number of items is 18, find the mean and standard deviation.
(a) 94, 1.53
(b) 93, 1.53
(c) 93, 1.55
(d) None of the above
Answer
B
Question: The variance of the numbers 2, 3, 11 and x is 49/4.
Find the value of x.
(a) 6, 14/3
(b) 6, 14/5
(c) 6, 16/3
(d) None of these
Answer
A
Question: If runs of two players A B and in 10 cricket matches are such that player A has mean 50 and variance 36 and player Bhas mean 60 and variance 81 of runs, then the player more consistent in runs is
(a) A
(b) B
(c) Both are equally consistent
(d) None of the above
Answer
A
Question: The marks of some students were listed out of 75.
The SD of marks was found to be 9. Subsequently the marks were raised to a maximum of 100 and variance of new marks was calculated. The new variance is
(a) 81
(b) 122
(c) 144
(d) None of these
Answer
C
Question: A batsman scores sums in 10 innings 38, 70, 48, 34, 42, 55, 46, 63, 54 and 44, then the deviation from median is
(a) 8.6
(b) 6.4
(c) 9.6
(d) 10.6
Answer
A
Question: In a college of 300 students every student reads 5 newspapers and every newspaper is read by 60 students. The number of newspapers are
(a) atleast 30
(b) atmost 20
(c) exactly 25
(d) None of these
Answer
C
Question: Consider any set of 201 observations x1,x2,…,x200,x201. It is given that x1<x2<…<x200<x201. Then, the mean deviation of this set of observations about a point k is minimum when k is equal to
(a) (x1 + x2 +…+ x200 + x201)/201
(b) x1
(c) x101
(d) x201
Answer
C
Question:
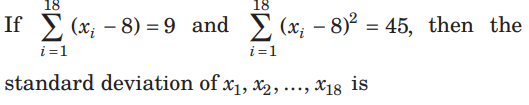
(a) 4/9
(b) 9/4
(c) 3/2
(d) None of these
Answer
C
Question: If the mean of a set of observations x1,x2,…,x10 …, is 20, then the mean of x1+ 4, x2 +8,…,x10+40 is
(a) 34
(b) 38
(c) 40
(d) 42
Answer
D
Question: The mean deviation from mean of the observation a, a+d,a+2d,…, a+2nd is
(a) n(n +1)d2
(b) n(n+1)/2 d2
(c) a + n(n+1)d2/2
(d) None of these
Answer
D
Question: If the standard deviation of x1, x2,…,xn is 3.5 then the standard deviation of -2x1-3,-2x2-3,…, -2xn -3 x n is
(a) -7
(b) -4
(c) 7
(d) 1.75
Answer
C
Question: If the mean of five observations x x+2, x+4, x+6 and x+8 and x + 8 is 11, then the mean of last three observations is
(a) 13
(b) 15
(c) 17
(d) None of these
Answer
A
Question: The first of two samples has 100 items with mean 15 and SD = 3. If the whole group has 250 items with mean 15.6 and SD = √13 44. , the SD of the second group is
(a) 4
(b) 5
(c) 6
(d) 3.52
Answer
A
Question:
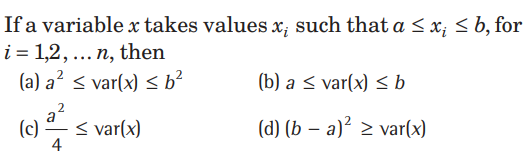
Answer
D
Question: The median of 19 observations of a group is 30. If two observations with values 8 and 32 are further included, then the median of the new group of 21 observations will be
(a) 28
(b) 30
(c) 32
(d) 34
Answer
B
Question: Following is the statement of marks obtained by two students A B and in 10 examination papers.
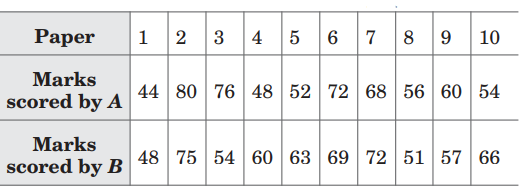
If the consistency of performance is the criterion for awarding a prize, find the prize winner among A B and .
(a) student A
(b) student B
(c) either students or A and B
(d) None of the above
Answer
B
Question: If the arithmetic mean of two unequal positive real numbers a and b a<b) be twice as their geometric mean, then a b: is equal to
(a) (2+√3):(√2+3)
(b) (2-√3): (2+√3)
(c) (2+√3): (2-√3)
(d) None of these
Answer
C
Question: The variable x takes two values x1 and x2 with frequencies f1 and f2, respectively. If σ denotes the standard deviation of x, then
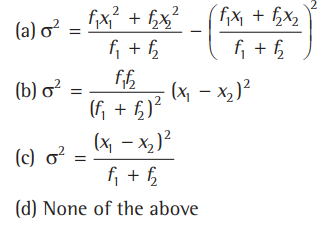
Answer
(A,B)
Question: There are 60 students in a class. The following is the frequency distribution of the marks obtained by the students in a test

where, x is a positive integer. Find the mean and standard deviation of the marks.
(a) 2.9, 1.14
(b) 2.8, 1.12
(c) 2.8, 1.18
(d) None of these
More Than One Correct Option
Answer
B
Question. The average of the squares of the numbers 0, 1, 2, 3, 4,…, n is
(a) 1/2 n(n+1)
(b) 1/6 n(2n+1)
(c) 1/6 (n+1)(2n+1)
(d) 1/6 n(n+1)
Answer
B
Question. If a variable takes the discrete values α + 4 , α -7/2 , α -5/2 , α-2 , α+1/2 ,α+5 (α > 0), then the median is
(a) α-5/4
(b) α-1/2
(c) α-2
(d) α+5/4
Answer
A
Question. Coefficient of skewness for the values Median = 18 8 . , Q1 = 14.6, Q3 = 25.2 is
(a) 0.2
(b) 0.5
(c) 0.7
(d) None of these
Answer
A
Question. Median of 2nC0 , 2nC1 ,2nC2 ,2nC3 …..,2nCn (where, n is even) is
(a) 2nCn/2
(b) 2nCn+1/2
(c) 2nCn-1/2
(d) None of these
Answer
A
Question. If MD is 12, the value of SD will be
(a) 75
(b) 12
(c) 24
d) None of these
Answer
A
Question. The mean of 5 observations is 4 and their variance is 5.2. If three If there observations are 1, 2 and 6, then the other two are
(a) 2 and 9
(b) 3 and 8
(c) 4 and 7
(d) 5 and 6
Answer
C
Question. If the sum of 11 consecutive natural numbers is 2761, then the middle number is
(a) 249
(b) 250
(c) 251
(d) 252
Answer
C
Question. If the mode of the data is 18 and the mean is 24, then median is
(a) 18
(b) 24
(c) 22
(d) 21
Answer
C
Question. If runs of two players A and B in 10 cricket matches are such that player A has mean 50 and variance 36 and player Bhas mean 60 and variance 81 of runs, then the player more consistent in runs is
(a) A
(b) B
(c) Both are equally consistent
(d) None of the above
Answer
B
Question. Mean and standard deviation of 100 observations were found to be 40 and 10, respectively. If at the time of calculation two observations were wrongly taken as 30 and 70 in place of 3 and 27, respectively, find the correct standard deviation.
(a) 10.20
(b) 10.24
(c) 10.29
(d) 10.27
Answer
B
Question. If in a moderately asymmetrical distribution mode and mean of the data are 6l and 9l respectively, then median is
(a) 8l
(b) 7l
(c) 6l
(d) 5l
Answer
A
Question. If the median of 21 observations is 40 and if the observations greater than the median are increased by 5, then the median of the new data will be
(a) 40
(b) 45
(c) 4+50/21
(d) 45-50/21
Answer
A
Question. The mean of n observations is x̄. If one observation xn + 1 is added, then the mean remains same. The value of xn + 1 is
(a) 0
(b) 1
(c) n
(d) x
Answer
D
Question. In a class of 100 students, the average amount of pocket money is ₹35 per student. If the average is ₹25 for girls and ₹50 for boys, then the number of girls in the class is
(a) 20
(b) 40
(c) 60
(d) 80
Answer
C
Question. The variance of the first n natural numbers is
(a) (n2 -1 /12)
(b) n(n2 -1 /12)
(c) (n2 +1 /12)
(d) n(n2 +1 /12)
Answer
A
Question. Standard deviations for first 10 natural numbers is
(a) 5.5
(b) 3.87
(c) 2.97
(d) 2.87
Answer
D
Question. In a moderately skewed distribution the values of mean and median are 5 and 6, respectively. The value of mode in such a situation is approximately equal to
(a) 8
(b) 11
(c) 16
(d) None of these
Answer
A
Question. Consider the following statements
I. The values of median and mode can be determined graphically.
II. Mean, median and mode have the same unit.
III. Range is the best measure of dispersion.
Which of these is/are correct?
(a) Only I
(b) Only II
(c) Both II and III
(d) None of these
Answer
A
Question. The quartile deviation of daily wages (in ₹) of 7 persons given below 12, 7, 15, 10, 17, 19 and 25 is
(a) 14.5
(b) 5
(c) 9
(d) 4.5
Answer
D
Question. If two variables x and y are such that 2y + 5 = 3x and Quartile Deviation (QD) of x is 8, then (QD) of y is
(a) 2
(b) 8
(c) 4
(d) None of these
Answer
D
Question. Find the quartile deviation of the following distribution.

(a) 8.20
(b) 8.25
(c) 8.30
(d) None of these
Answer
B
Question. Let G1 and G2 be the … geometric means of two … series x1, x2,…, x n; y1, y2 …,yn . IfG is the geometric mean of xi/yi ,i = 1, 2 , …, n. Then, G is equal to
(a) G1 – G2
(b) logG1 /logG2
(c) G1 / G2
(d) log(G1/G2)
Answer
C
Question. Geometric mean of first group of 4 observations is 8 and that of second group of 3 observations is 1024.
Then, geometric mean of all the 7 observations is
(a) 64
(b) 32
(c) 128
(d) None of these
Answer
A
Question. For a series the value of mean deviation is 15, the most likely value of its quartile deviation is
(a) 12.5
(b) 11.6
(c) 13
(d) 9.7
Answer
A
Question. The mean deviation of the data 3, 10, 10, 4, 7, 10, 5 from the mean is
(a) 2
(b) 2.57
(c) 3
(d) 3.75
Answer
B
Question. When tested, the lives (in hours) of 5 bulbs were noted as follows 1357, 1090, 1666, 1494, 1623
The mean deviations (in hours) from their mean is
(a) 178
(b) 179
(c) 220
(d) 356
Answer
A
Question. Following are the marks obtained by 9 students in a Mathematics test 50, 69, 20, 33, 53, 39, 40, 65, 59
The mean deviation from the median is
(a) 9
(b) 10.5
(c) 12.67
(d) 14.76
Answer
C
Question. Find the mean deviation about the mean of the set of first n natural numbers when n is an odd number.
(a) n2+1/4n
(b) n2-1/4n
(c) n2-3/5n
(d) None of these
Answer
B
Question. Find the mean deviation from the median of the following data

(a) 7.08
(b) 7
(c) 7.1
(d) 7.05
Answer
B
Question. The standard deviation of the data 6, 5, 9, 13, 12, 8, 10 is (diagram)
(a) √(52/7)
(b) (52/7)
(c) √6
(d) 6
Answer
A
Question. The mean of 100 observations is 50 and their standard deviation is 5. The sum of all squares of all the observations is
(a) 50000
(b) 250000
(c) 252500
(d) 255000
Answer
C
Question. Let a, b, c, d and e be the observations with mean m and standard deviation S. The standard deviation of the observations a + k, b + k, c + k, d + k, e + k is
(a) S
(b) kS
(c) S + k
(d) S/k
Answer
A
Question. The SD of 15 items is 6 and if each item is decreases by 1, then standard deviation will be
(a) 5
(b) 7
(c) 91/15
(d) 6
Answer
D
67. If SD of X is S, then SD of the variable μ = aX+b/c, where a, b and c are constants, is

Answer
B
Question. If x is the arithmetic mean of n independent variates x1 x2 x3 ….xn, each of the standard deviation σ, then variance (x̄) is
(a) σ2/n
(b) nσ2
(c) (n + 1)σ2/3
(d) None of these
Answer
A
Question. Let x1, x2, x3, x4, x5 and be the observations with mean m and standard deviation S. The standard deviation of the observations kx1 , kx2 , kx3 , kx4 , kx5 and is
(a) k + S
(b) S/k
(c) kS
(d) S
Answer
C
Question. Let x1 , x2 . . . , be n observations. Let w lx k i i = + for i = 1, 2, . .. , n, where l and k are constants. If the mean of xi’s is 48 and their standard deviation is 12, the mean of wi’s is 55 and standard deviation of wi ’s is 15, the values of l and k should be
(a) l = 1.25, k = – 5
(b) l = -1.25, k = 5
(c) l = 2.5, k = – 5
(d) l = 2.5, k = 5
Answer
A
Question. Consider the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. If 1 is added to each number, then variance of the numbers so obtained is
(a) 6.5
(b) 2.87
(c) 3.87
(d) 8.25
Answer
D
Question. The following information relates to a sample of size 60 : ∑x2 = 18000, ∑x = 960.The variance is
(a) 6.63
(b) 16
(c) 22
(d) 44
Answer
D
Question. Coefficient of variation of two distributions are 50 and 60 and their arithmetic means are 30 and 25 respectively. Difference of their standard deviation is
(a) 0
(b) 1
(c) 1.5
(d) 2.5
Answer
A
Question. If the variance of 1, 2, 3, 4, 5, . . . , 10 is 99/12 , then the standard deviation of 3, 6, 9, 12, . . . , 30 is
(a) 297/4
(b) 3/2(√33)
(c) 3/2(√99)
(d) √(99/12)
Answer
B
Question. The mean and standard deviation of some data for the time taken to complete a test are calculated with the following results
Number of observations = 25, mean = 18.2 s,
standard deviation = 3.25 s.
Further, another set of 15 observations x1 x2 x15 . . also in seconds, is now available and we have i=1∑15xi = 279 and i=1∑15x2i = 5524. Find the standard deviation based on all 40 observations.
(a) 3.80
(b) 3.87
(c) 3.70
(d) None of these
Answer
B
Question. The variance of the numbers 2, 3, 11 and x is 49/4 Find the value of x.
(a) 6,14/3
(b) 6,14/5
(c) 6,16/3
(d) None of these
Answer
A
Question. The marks of some students were listed out of 75.
The SD of marks was found to be 9. Subsequently the marks were raised to a maximum of 100 and variance of new marks was calculated. The new variance is
(a) 81
(b) 122
(c) 144
(d) None of these
Answer
C
Question. A batsman scores sums in 10 innings 38, 70, 48, 34,42, 55, 46, 63, 54 and 44, then the deviation from median is
(a) 8.6
(b) 6.4
(c) 9.6
(d) 10.6
Answer
A
Question. Consider any set of 201 observations x1, x2….. x200 ,x201. It is given that x1< x2<….. x200.< x201. Then, the mean deviation of this set of observations about a point k is minimum when k is equal to
(a) (x1 + x2 + K + x200 + x201) / 201
(b) x1
(c) x101
(d) x201
Answer
C
Question. In a college of 300 students every student reads 5 newspapers and every newspaper is read by 60 students. The number of newspapers are
(a) atleast 30
(b) atmost 20
(c) exactly 25
(d) None of these
Answer
C
Question. If the mean of a set of observations x x x 1 2 10 , , …, is 20,then the mean of x x x 1 2 10 + 4, + 8, …, + 40 is
(a) 34
(b) 38
(c) 40
(d) 42
Answer
D
Question. If i=1∑18 (xi – 8) = 9 and i=1∑18 (xi – 8)2 = 45,, then the standard deviation of x1 , x2 ,x18 …, is
(a) 4/9
(b) 9/4
(c) 3/2
(d) None of these
Answer
C

We hope you liked the above provided MCQ Questions Chapter 15 Statistics Class 11 Mathematics with solutions. If you have any questions please ask us in the comments box below.

