Please refer to MCQ Questions Chapter 13 Probability Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 13 Probability in Class 12 Mathematics provided below to get more marks in exams.
Chapter 13 Probability MCQ Questions
Question. If the chance that a ship arrives safely at a port is 9/10 ; the chance that out of 5 expected ships, at least 4 will arrive safely at the port 2, is
(a) 91854/100000
(b) 32805/100000
(c) 59049/100000
(d) 26244/100000
Answer
A
Question. The probability that a man hits a target is p = 0.1. He fires n = 100 times. The expected number n of times he will hit the target is :
(a) 33
(b) 30
(c) 20
(d) 10
Answer
D
Question. Let three fair coins be tossed. Let A = {all heads or all tails}, B = {atleast two heads}, and C = {atmost two tails}.
Which of the following events are independent?
(a) A and C
(b) B and C
(c) A and B
(d) None of these
Answer
C
Question. For a loaded die, the probabilities of outcomes are given as under.
P(1) = P (2) = 0.2
P(3) = P (5) = P(6) = 0.1 and P(4) = 0.3
The dice is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is 10 or more’’ respectively. Then, match the terms of column I with their respective values in column II.

Codes
A B C D
(a) 4 3 2 1
(b) 4 3 1 5
(c) 4 1 3 5
(d) 2 4 1 3
Answer
A
Question. If P(A∩B) = 0.15 , P(B’) = 0.10 , then P(A/B) =
(a) 1/3
(b) 1/4
(c) 1/6
(d) 1/5
Answer
C
Question. P(E∩F) is equal to
(a) P(E). P(F|E)
(b) P(F). P(E|F)
(c) Both (a) and
(b) (d) None of these
Answer
C
Question. The probability of a man hitting a target is 1/4. The number of times he must shoot so that the probability he hits the target, at least once is more than 0.9, is [use log 4 = 0.602 and log 3 = 0.477]
(a) 7
(b) 8
(c) 6
(d) 5
Answer
B
Question. If P(A) = 2/5, P(B) = 3/10 and P(A ∩ B) = 1/5, then P(A’ | B’) . P(B’ | A’) is equal to
(a) 5/6
(b) 5/7
(c) 25/42
(d) 1
Answer
C
Question. A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}.

Codes
A B C
(a) 2 3 1
(b) 1 2 3
(c) 2 1 3
(d) 3 1 2
Answer
A
Question. If X follows Binomial distribution with mean 3 and variance 2, then P(X ≥ 8) is equal to :
(a) 17/39
(b) 18/39
(c) 19/39
(d) 20/39
Answer
C
Question. Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is
(a) 0.2
(b) 0.7
(c) 0.06
(d) 0.14
Answer
D
Question. In a meeting, 70% of the members favour and 30% oppose a certain proposal. A member is selected at random and we take X = 0, if he opposed and X = 1, if he is in favour. Then, E(X) and Var (X) respectively are
(a) 3/7, 5/17
(b) 13/15, 2/15
(c) 7/10, 21/100
(d) 7/10, 23/100
Answer
C
Question. The mean and variance of a random variable X having binomial distribution are 4 and 2 respectively, then P (X = 1) is
(a) 1/4
(b) 1/32
(c) 1/16
(d) 1/8
Answer
B
Question. Given, two independent events A and B such that P(A) = 0.3, P(B) = 0.6. Then, match the terms of column I with their respectively values in column II .
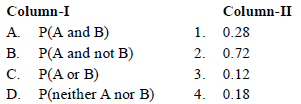
Codes
A B C D
(a) 4 3 1 2
(b) 4 2 1 3
(c) 1 2 3 4
(d) 4 3 2 1
Answer
D
Question. Suppose X follows a binomial distribution with parameters n and p, where 0 < p < 1, if P(X = r)/P(X = n – r) is independent of n and r, then
(a) p = 1/2
(b) p = 1/3
(c) p = 1/4
(d) None of these
Answer
A
Question. There is 30% chance that it rains on any particular day. Given that there is at least one rainy day, then the probability that there are at least two rainy days is
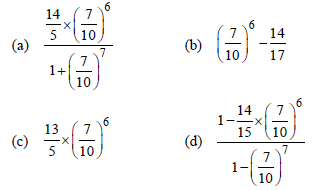
Answer
D
Question. The mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is
(a) 1
(b) 2
(c) 5
(d) 8/3
Answer
B
Question. Two dice are thrown. If it is known that the sum of the numbers on the dice is less than 6, the probability of getting a sum 3 is
(a) 1/8
(b) 2/5
(c) 1/5
(d) 5/18
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Answer
B
Question. A signal which can be green or red with probability 4/5 and 1/5 respectively, is received by station A and then trasmitted to station B. The probability of each station receiving the signal correctly is 3/4. If the signal received at station B is given, then the probability that the original signal is green, is
(a) 3/5
(b) 6/7
(c) 20/23
(d) 9/20
Answer
A
Question. If P(B) = 3/5 , P(A | B) = 1/2 and P(A ∪ B) = 4/5 , then P(A∪B)’ + P(A’∪B) =
(a) 1/5
(b) 4/5
(c) 1/2
(d) 1
Answer
D
Question. The probability of the simultaneous occurrence of two events A and B is p. If the probability that exactly one of the events occurs is q, then which of the following is not correct?
(a) P(A’) + P(B’) = 2 + 2q − p
(b) P(A’) + P(B’) = 2 − 2p − q
(c) P(A ∩ B | A ∪ B) = p/p+q
(d) P(A’∩ B’) = 1− p − q
Answer
A
Question. Which one is not a requirement of a binomial distribution?
(a) There are 2 outcomes for each trial
(b) There is a fixed number of trials
(c) The outcomes must be dependent on each other
(d) The probability of success must be the same for all the trial
Answer
C
Question. Bag P contains 6 red and 4 blue balls and bag Q contains 5 red and 6 blue balls. A ball is transferred from bag P to bag Q and then a ball is drawn from bag Q. What is the probability that the ball drawn is blue?
(a) 7/15
(b) 8/15
(c) 4/19
(d) 8/19
Answer
B
Question. In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6. Then, the probability that he will knock down fewer than 2 hurdles is
(a) 59/2×69
(b) 510/2×610
(c) 59/2×610
(d) 510/2×69
Answer
D
Question. Two dice are thrown, simultaneously. If X denotes the number of sixes, then the expected value of X is
(a) E(X) = 1/3
(b) E(X) = 2/3
(c) E(X) = 1/6
(d) E(X) = 5/6
Answer
A
Question. If A and B are two events such that P(A) ≠ 0 and

Answer
C
Question. Three persons, A, B and C, fire at a target in turn, starting with A. Their probability of hitting the target are 0.4, 0.3 and 0.2 respectively. The probability of two hits is
(a) 0.024
(b) 0.188
(c) 0.336
(d) 0.452
Answer
B
Question. A and B are events such that P (A/B) = P (B/A) then
(a) A ⊂ B
(b) B = A
(c) A ∩ B = Φ
(d) P(A) = P (B)
Answer
D
Question. Coloured balls are distributed in four boxes as shown in the following table
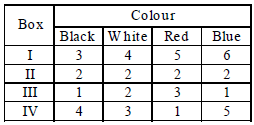
A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black.
Probability that the ball drawn from Box III, is
(a) 0.161
(b) 0.162
(c) 0.165
(d) 0.104
Answer
C
Question. Two integers are selected at random from the set {1, 2, …., 11}. Given that the sum of selected numbers is even, the conditional probability that both the numbers are even is :
(a) 7/10
(b) 1/2
(c) 2/5
(d) 3/5
Answer
C
Question. An unbiased coin is tossed. If the outcome is a head then a pair of unbiased dice is rolled and the sum of the numbers obtained on them is noted. If the toss of the coin results in tail then a card from a well-shuffled pack of nine cards numbered 1, 2, 3, …, 9 is randomly picked and the number on the card is noted. The probability that the noted number is either 7 or 8 is:
(a) 13/36
(b) 15/72
(c) 19/72
(d) 19/36
Answer
C
Question. Let A, B, C, be pairwise independent events with P (C) > 0 and P( A ∩ B ∩ C) =0. Then P(Ac ∩ Bc / C).
(a) P(Bc) – P(B)
(b) P(Ac) + P(Bc)
(c) P(Ac) – P(B)
(d) P(Ac) – P(B)
Answer
D
Question. If C and D are two events such that C ⊂ D and P(D) ≠ 0, then the correct statement among the following is
(a) P(C | D) ≥ P(C)
(b) P(C | D) < P(C)
(c) P(C | D) = P(D)/P(C)
(d) P(C | D) = P(C)
Answer
A
Question. Let EC denote the complement of an event E. Let E1, E2 and E3 be any pairwise independent events with P(E1) > 0 and P(E1 ∩ E2 ∩ E3 ) = 0. Then P(E2C ∩ E3C / E1 ) is equal to :
(a) P(E2C) + P(E3)
(b) P(E3C) – P(E2C)
(c) P(E3) – P(E2C)
(d) P(E3C) – P(E2)
Answer
D
Question. An unbiased coin is tossed 5 times. Suppose that a variable X is assigned the value k when k consecutive heads are obtained for k = 3, 4, 5, otherwise X takes the value –1. Then the expected value of X, is:
(a) 3/16
(b) 1/8
(c) − 3/16
(d) − 1/8
Answer
B
Question. Assume that each born child is equally likely to be a boy or a girl. If two families have two children each, then the conditional probability that all children are girls given that at least two are girls is:
(a) 1/11
(b) 1/10
(c) 1/12
(d) 1/17
Answer
A
Question. Minimum number of times a fair coin must be tossed so that the probability of getting at least one head is more than 99% is :
(a) 5
(b) 6
(c) 8
(d) 7
Answer
D
Question. Let A and E be any two events with positive probabilities:
Statement – 1: P(E/A) ≥ P(A/E) P(E)
Statement – 2: P(A/E) ≥ P(A ∩ E)
(a) Both the statements are true
(b) Both the statements are false
(c) Statement-1 is true, Statement-2 is false
(d) Statement-1 is false, Statement-2 is true
Answer
A
Question. A, B, C try to hit a target simultaneously but independently. Their respective probabilities of hitting the targets are 3/4, 1/2, 5/8. The probability that the target is hit by A or B but not by C is :
(a) 21/64
(b) 7/8
(c) 7/32
(d) 9/64
Answer
A
Question. The minimum number of times one has to toss a fair coin so that the probability of observing at least one head is at least 90% is :
(a) 5
(b) 3
(c) 4
(d) 2
Answer
C
Question. The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 successes is
(a) 2/256
(b) 219/256
(c) 128/256
(d) 37/256
Answer
A
Question. A random variable X has the probability distribution:
(image 66)
For the events E = {X is a prime number } and F = {X < 4}, the P(E ∪ F) is
(a) 0.50
(b) 0.77
(c) 0.35
(d) 0.87
Answer
B
Question. In a random experiment, a fair die is rolled until two fours are obtained in succession. The probability that the experiment will end in the fifth throw of the die is equal to :
(a) 200/65
(b) 150/65
(c) 225/65
(d) 175/65
Answer
D
Question. In a game, a man wins ₹ 100 if he gets 5 or 6 on a throw of a fair die and loses ₹ 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is :
(a) (400/9)loss
(b) 0
(c) (400/3)gain
(d) (400/3)loss
Answer
C
Question. In a game two players A and B take turns in throwing a pair of fair dice starting with player A and total of scores on the two dice, in each throw is noted. A wins the game if he throws a total of 6 before B throws a total of 7 and B wins the game if he throws a total of 7 before A throws a total of six. The game stops as soon as either of the players wins. The probability of A winning the game is :
(a) 5/31
(b) 31/61
(c) 5/6
(d) 30/61
Answer
D
Question. In a bombing attack, there is 50% chance that a bomb will hit the target. At least two independent hits are required to destroy the target completely. Then the minimum number of bombs, that must be dropped to ensure that there is at least 99% chance of completely destroying the target, is _________.
Answer
1100
Question. The probability of a man hitting a target is 1/10. The least number of shots required, so that the probability of his hitting the target at least once is greater than 1/4, is ___________.
Answer
3.00
Question. A die is thrown two times and the sum of the scores appearing on the die is observed to be a multiple of 4. Then the conditional probability that the score 4 has appeared atleast once is :
(a) 1/4
(b) 1/3
(c) 1/8
(d) 1/9
Answer
D
Question. If the probability of hitting a target by a shooter, in any shot, is 1/3, then the minimum number of independent shots at the target required by him so that the probability of hitting the target at least once is greater than 5/6, is:
(a) 3
(b) 6
(c) 5
(d) 4
Answer
C
Question. Let a random variable X have a binomial distribution with mean 8 and variance 4. If P(X d” 2) = k/216, then k is equal to:
(a) 17
(b) 121
(c) 1
(d) 137
Answer
D
Question. A person throws two fair dice. He wins Rs. 15 for throwing a doublet (same numbers on the two dice), wins Rs. 12 when the throw results in the sum of 9, and loses Rs. 6 for any other outcome on the throw. Then the expected gain/loss (in Rs.) of the person is :
(a) (1/2)gain
(b) (1/4)loss
(c) (1/2)loss
(d) 2 gain
Answer
C
Question. Two cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Let X denote the random variable of number of aces obtained in the two drawn cards. Then P(X = 1) + P(X = 2) equals:
(a) 49/169
(b) 52/169
(c) 24/169
(d) 25/169
Answer
D
Question. An urn contains 5 red and 2 green balls. A ball is drawn at random from the urn. If the drawn ball is green, then a red ball is added to the urn and if the drawn ball is red, then a green ball is added to the urn; the original ball is not returned to the urn. Now, a second ball is drawn at random from it. The probability that the second ball is red is:
(a) 21/49
(b) 27/49
(c) 26/49
(d) 32/49
Answer
D
Question. A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is
(a) 8/729
(b) 8/243
(c) 1/729
(d) 8/9
Answer
B
Question. A coin is tossed three times is succession. If E is the event that there are at least two heads and F is the event in which first throw is a head, then P(E/F) equal to:
(a) 3/4
(b) 3/8
(c) 1/2
(d) 1/8
Answer
A
Question. Five bad eggs are mixed with 10 good ones. If three eggs are drawn one by one with replacement, then the probability distribution of the number of good eggs drawn, is
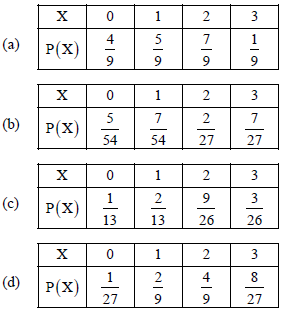
Answer
D
Question. If two events A and B are such that P(A’) = 0.3, P(B) = 0.4 and P(A∩B’) = 0.5, then
P (B/A ∪ B) =
(a) 1/4
(b) 1/5
(c) 3/5
(d) 2/5
Answer
A
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, Reason is correct; Reason is a correct explanation for assertion.
(b) Assertion is correct, Reason is correct; Reason is not a correct explanation for Assertion
(c) Assertion is correct, Reason is incorrect
(d) Assertion is incorrect, Reason is correct.
Question. Let A and B be two events associated with an experiment such that
P(A∩B) = P(A)P(B)
Assertion : P(A|B) = P(A) and P(B|A) = P(B)
Reason : P(A∪B) = P(A) + P(B)
Answer
C
Question. Consider the two events E and F which are associated with the sample space of a random experiment.
Assertion : P(E / F) = n (E ∩ F)/n (F).
Reason : P(E / F) = n (E ∩ F)/P(F).
Answer
A
Question. Consider the following statements
Assertion : Let A and B be two independent events. Then P(A ∩ B) = P(A) + P(B)
Reason : Three events A, B and C are said to be independent, if P (A ∩ B ∩ C) = P(A) P(B) P(C).
Answer
D
Question. Assertion : For a binomial distribution B(n, p), Mean > Variance
Reason : Probability is less than or equal to 1
Answer
A
Question. Assertion : The mean of a random variable X is also called the expectation of X, denoted by E(X).
Reason : The mean or expectation of a random variable X is not sum of the products of all possible values of X by their respective probabilities.
Answer
C
Question. Assertion : Consider the experiment of drawing a card from a deck of 52 playing cards, in which the elementary events are assumed to be equally likely.
If E and F denote the events the card drawn is a spade and the card drawn is an ace respectively.
then P(E|F) = 1/4 and P(F|E) = 1/13
Reason : E and F are two events such that the probability of occurrence of one of them is not affected by occurrence of the other. Such events are called independent events.
Answer
A

