Please refer to MCQ Questions Chapter 9 Circles Class 10 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 10 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 10 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 9 Circles in Class 10 Mathematics provided below to get more marks in exams.
Chapter 9 Circles MCQ Questions
Please refer to the following Chapter 9 Circles MCQ Questions Class 10 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 9 Circles Class 10 Mathematics
Question. In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
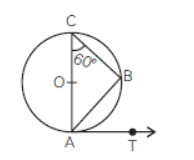
(a) 30°
(b) 60°
(c) 75°
(d) 105°
Answer
B
Question. In the figure, TP and TQ are tangents drawn to the circle with centre at O. If ∠POQ = 115° then ∠PTQ is:
(a) 115°
(b) 57.5°
(c) 55°
(d) 65°
Answer
D
Question. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm2
(b) 65 cm2
(c) 30 cm2
(d) 32.5 cm2
Answer
A
Question. The chord of a circle of radius 10 cm subtends a right angle at its centre. The length of the chord (in cm) is ?

(a) 10 cm
(b) 10√2 cm
(c) 20 cm
(d) 12 cm
Answer
B
Question. If radii of concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
(a) 8 cm
(b) 6 cm
(c) 10 cm
(d) 12 cm
Answer
B
Question. In a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If O is the centre of the circle, then length OP is ?
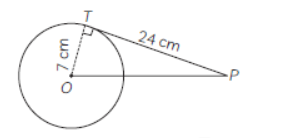
(a) 25 cm
(b) 15 2
(c) 10 cm
(d) 10 cm
Answer
A
Question. tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
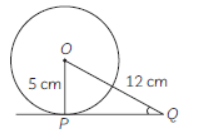
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) √119 cm
Answer
D
Question. In the given figure, if ∠AOB = 125°, then ∠COD is equal tox
(a) 62.5°
(b) 45°
(c) 35°
(d) 55°
Answer
D
Question. From an enternal point Q, the length of the tangents to a circle is 5 cm and the distance of Q from the centre is 5 cm. The radius of the circle is
(a) 39 cm
(b) 3 cm
(c) 39 cm
(d) 7 cm
Answer
C
Question. At one end A of diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
Answer
D
Question. In the figure. PQ is a tangent to the circle with centre at O, at the point B. If ∠AOB = 100°, then ∠ABP is equal tox
(a) 50°
(b) 40°
(c) 60°
(d) 80°
Answer
A
Question. In the given figure, AT is a tangent to the circle with centre ‘O; such that OT = 4 cm and ∠OTA = 30°. Then AT is equal tox

(a) 4 cm
(b) 2 cm
(c) 2 √3cm
(d) 4 √3cm
Answer
C
Question. In the figure, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR = 90°, the length of PQ is :

(a) 3 cm
(b) 4 cm
(c) 2 cm
(d) 2√ 2 cm
Answer
B
Question. From an external point A, two tangents AB and AC are drawn to the circle with centre O. Then OA is the perpendicular bisector of
(a) BC
(b) AB
(c) AC
(d) none of these
Answer
A
Question. If the radii of two concentric circles are 6 cm and 10 cm, the length of chord of the larger circle which is tangent to other is
(a) 14 cm
(b) 16 cm
(c) 18 cm
(d) 12 cm
Answer
B
Question. In the given figure, the length PB is equal to
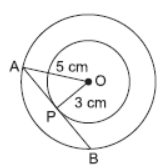
(a) 2 cm
(b) 7 cm
(c) 6 cm
(d) 4 cm
Answer
D
Question. In the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ = 110°, then ∠PTQ is

(a) 110°
(b) 90°
(c) 80°
(d) 70°
Answer
D
Question. In the given figure, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR = 90°, then length of PQ is
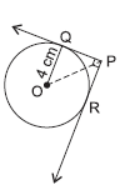
(a) 3 cm
(b) 4 cm
(c) 2 cm
(d) 2 2 cm
Answer
B
In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Question. Assertion (A): When two tangents are drawn to a circle from an external point, they subtend equal angles at the centre.
Reason (R): A parallelogram circumscribing a circle is a rhombus.
Answer
B
Question. Assertion (A): PA and PB are two tangents to a circle with centre O such that ∠AOB = 110°, then ∠APB = 90°.
Reason (R): The length of two tangents drawn from an external point are equal.
Answer
D
Fill in the Blanks :
Question. ABCD is a cyclic quadrilateral. If ∠BAC = 50° and ∠DBC = 60° then ∠BCD = ………………….. .
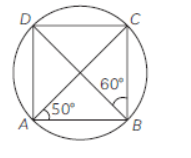
Answer
70º
Question. Secant intersects a circle at ………………….. distinct points.
Answer
Secant intersects a circle at two distinct points
Question. From an enternal point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then ∠AOB = ………………….. .
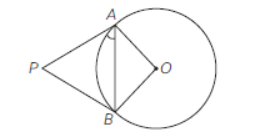
Answer
100º 17
Question. All concentric circles are ………………….. to each other.

Answer
Similar
Question. The length of the tangent to a circle from a point P, which is 25 cm away from the centre, is 24 cm. The radius of the circle is ……………………
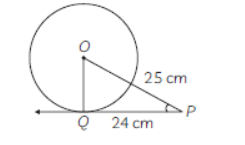
Answer
7 cm 19
Question. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 13 cm. Then, the length PQ is ………………….. .
Answer
12 cm
Question. PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°, then ∠OPQ = ……………………
Answer
30º 18
Question. In the given figure the length PB = …………………………. cm.
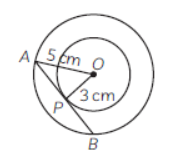
Answer
4 cm 22
True or False :
Question. AB is the diameter of a circle and AC is its chord such that ΔBAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
Answer
True
Question. If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is also 60°.
Answer
False
Question. The tangent to the circumcircle of an isosceles ΔABC at A, in which AB = AC, is parallel to BC.
Answer
True
Question. If a number of circles pass through the end points P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
Answer
True
Question. The length of the tangent from an enternal point P on a circle with centre O is always less than OP.
Answer
True
Question. If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular: bisector of PQ.
Answer
False
Question. The angle between two tangents to a circle may be 0°.
Answer
True
Question. The length of tangent from an enternal point on a circle is always greater than radius of the circle.
Answer
False
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
Question. Assertion: If in a cyclic quadrilateral, one angle is 40°, then the opposite angle is 140°
Reason: Sum of opposite angles in a cyclic quadrilateral is equal to 360°
Answer
C
Question. Assertion: If length of a tangent from an external point to a circle is 8 cm, then length of the other tangent from the same point is 8 cm.
Reason: length of the tangents drawn from an external point to a circle are equal.
Answer
A
Question. Assertion: If in a circle, the radius of the circle is 3 cm and distance of a point from the centre of a circle is 5 cm, then length of the tangent will be 4 cm.
Reason:(hypotenuse)2 = (base)2 + (height)2
Answer
A

We hope you liked the above provided MCQ Questions Chapter 9 Circles Class 10 Mathematics with solutions. If you have any questions please ask us in the comments box below.


