See below CBSE Class 12 Physics Term 1 Sample Paper Set D with solutions. We have provided CBSE Sample Papers for Class 12 Physics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Physics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Physics examination.
CBSE Sample Paper for Class 12 Physics Term 1 Set D
SECTION – A
Question 1. What is the function of a photodiode?
Answer.Photodiode is used to detect the light signal and to measure light intensity.
Question 2. Can the potential function have a maximum or minimum value in free space?
Answer.No, potential function cannot have a maximum or minimum value in free space.
For that to happen dV/dr = 0 or E = 0 which is not so in free space.
Question 3. In a half wave rectifier circuit operating from 50 Hz mains frequency, what would be the fundamental frequency in the ripple?
Answer.As the output voltage obtained in a half wave rectifier circuit has a single variation in one cycle of ac voltage, hence the fundamental frequency in the ripple of output voltage would be = 50 Hz.
Question 4. A steady current flows in a metallic conductor of non-uniform cross-section. Which of the following quantities is/are constant along the length of conductor : current, current density, drift speed?
OR
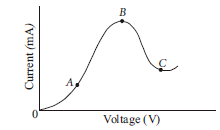
The graph shown in the figure represents a plot of current versus voltage for a given semiconductor. Identify
the region, if any, over which the semiconductor has a negative resistance.
Answer.
Total current remains the same, current density J = I/A , J changes with change in area, drift speed vd = I/Ane also changes.
OR
Region BC of the graph has a negative slope, hence in region BC semiconductor has a negative resistance.
Question 5. Why is the penetrating power of gamma rays very large?
OR
Welders wear special goggles or face masks with glass windows to protect their eyes from electromagnetic radiations. Name the radiations and write the range of their frequency.
Answer.g-rays are electromagnetic waves of very large energy, so they passes through the matter with less number of collisions with atoms or molecules of matter, thereby penetrating more into it.
OR
Ultraviolet radiations produced during welding are harmful to eyes. Special goggles or face masks are used to protect eyes from UV radiations. UV radiations have a range of frequency between 1014 Hz – 1016 Hz.
Question 6. Define the term ‘coherent sources’ which are required to produce interference pattern in Young’s double slit experiment.
Answer. Two sources are said to be coherent, if they emit light waves of same frequency or wavelength and of a stable phase difference.
Question 7. A magnetic needle, free to rotate in a vertical plane, orients itself vertically at a certain place on the Earth.
What are the values of
(i) horizontal component of Earth’s magnetic field and
(ii) angle of dip at this place?
OR
At a place, the horizontal component of earth’s magnetic field is B and angle of dip is 60°. What is the value
of horizontal component of the earth’s magnetic field at equator?
Answer.(i) Zero, (ii) 90°
OR

Question 8. In a series LCR circuit, the voltages across an inductor, a capacitor and a resistor are 30V, 30V and 60V respectively. What is the phase difference between the applied voltage and the current in the circuit.
Answer.As VL = VC = 30 V, so the series LCR circuit is in resonance and hence the applied voltage and current in the circuit are in same phase.
Question 9. Which process causes depletion region in a p-n junction?
OR
Why cannot we use Si and Ge in fabrication of visible LEDs?
Answer.Diffusion of electrons and holes across the junction.
OR
LED’s must have band gap in the order of 1.8 eV to 3 eV but Si and Ge have band gap less than 1.8 eV.
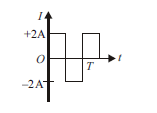
Question 10. Calculate the rms value of the alternating current shown in the figure.
For question numbers 11, 12, 13 and 14, two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Answer.2 A, because magnitude of current is constant at 2 A.
Question 11. Assertion (A) : Faraday’s laws are consequences of conservation of energy.
Reason (R) : In a purely resistive A.C. circuit, the current lags behind the e.m.f.
Answer
C
Question 12. Assertion (A) : Voltmeter is connected in parallel with the circuit.
Reason (R) : Resistance of a voltmeter is very large.
Answer
A
Question 13. Assertion (A) : Charge never flows from a condenser of higher capacity to the condenser of lower capacity.
Reason (R) : Flow of charge between two bodies connected by a thin wire is determined by the charges on them.
Answer
D
Question 14. Assertion (A) : The possibility of an electric bulb fusing is higher at the time of switching on and off.
Reason (R) : Inductive effects produce a surge at the time of switch-off and switch-on.
Answer
A
SECTION – B
Questions 15 and 16 are Case Study based questions and are compulsory. Attempt any 4 sub parts from each question. Each question carries 1 mark.
Question 15. Niels Bohr introduced the atomic Hydrogen model in 1913. He described it as a positively charged nucleus,comprised of protons and neutrons, surrounded by a negatively charged electron cloud. In the model, electrons orbit the nucleus in atomic shells. The atom is held together by electrostatic forces between the positive nucleus and negative surroundings.
(i) In the Bohr model of the hydrogen atom, discrete radii and energy states result when an electron circles the atom in an integer number of
(a) de Broglie wavelengths
(b) wave frequencies
(c) quantum numbers
(d) diffraction patterns.
Answer
C
(ii) Which of the following was explained by the Bohr atom?
(a) Atomic spectra.
(b) The fact that most of the mass of an atom is in the nucleus.
(c) Nuclear fission.
(d) The photoelectric effect.
Answer
A
(iii) In Bohr’s model of the hydrogen atom, the radius of an orbit _____.
(a) is proportional to n2
(b) is smallest for the highest energy state
(c) increases when a photon of light is emitted from an excited atom
(d) can have any value that is larger than the ground-state radius
Answer
A
(iv) The energy associated with the first orbit in the hydrogen atom is −2.17 × 10−18 J atom−1. What is the energy associated with the fifth orbit?
(a) −8.77 × 10–20 J atom–1
(b) −9.34 × 10–20 J atom–1
(c) −7.65 × 10–20 J atom–1
(d) −8.77 × 10–24 J atom–1
Answer
A
(v) Suppose the energy required to remove all the three electrons from a lithium atom in the ground state is ‘E’ electron volt. What will be the energy required (in electron volt) to remove two electrons from the lithium atom in the ground state?
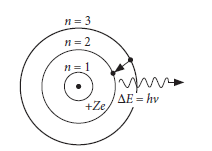
(a) 2E/3
(b) E – 13.6
(c) E – 27.2
(d) E – 122.4
Answer
D
Question 16. When the capacitor is connected to the battery, the energy stored in the air-filled capacitor is U = 1/2 CV2, and the charge on each plate is q = CV. When the capacitor is filled with the dielectric material, its capacitance becomes kC, where k is the dielectric constant of the material. This increases the charge stored on each plate to kCV. The additional charge of (k – 1)CV came through the battery, which did some work, given by ΔqV = (k – 1)CV2.
(i) What is the value of total capacitance if two dielectric slabs are introduced between the plates of the capacitor as shown?
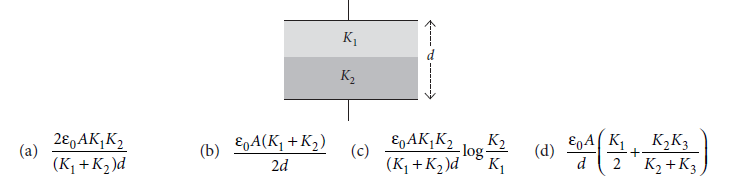
Answer
A
(ii) What is the value of total capacitance if two dielectric slabs are introduced between the plates of the capacitor as shown?

Answer
B
(iii) What is the value of total capacitance if two dielectric slabs are introduced between the plates of the capacitor as shown?
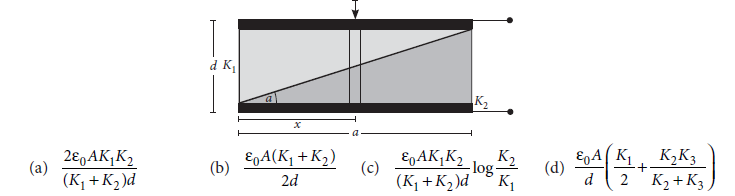
Answer
C
(iv) What is the value of total capacitance if two dielectric slabs are introduced between the plates of the capacitor as shown?
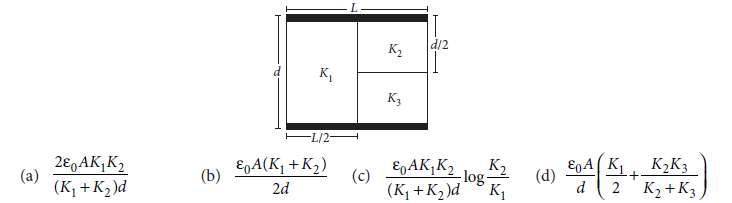
Answer
D
(v) Two identical conducting plates of plate area A are separated by a distance d to form a parallel plate air capacitor. Now a metal sheet of thickness d/3 is inserted between the plates of the capacitor. The ratio of capacitance before the insertion of plate and after the insertion of plate is
(a) 2:3
(b) 1:1
(c) 3:1
(d) 4:1
Answer
A
SECTION – C
Question 17. A sphere S1 of radius r1 encloses a net charge Q. If there is another concentric sphere S2 of radius r2(r2 > r1) enclosing charge 3Q, find the ratio of the electric flux through S1 and S2. How will the electric flux through sphere S1 change if a medium of dielectric constant 5 is introduced in the space inside S1 in place of air?

OR
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
Answer.

Question 18. The figure shows a modified Young’s double slit experimental set-up. Here SS2 – SS1 = l/4.

(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
Answer.

Question 19. Draw energy band diagram of p and n type semiconductors. Also write two differences between p and n type semiconductors.
OR
Energy gap in a p – n photodiode is 2.8 eV. Can it detect a wavelength of 600 nm? Justify your answer.
Answer.

Question 20. A fish in a water tank sees the outside world as if it (the fish) is at the vertex of a cone such that the circular base of the cone coincides with the surface of water. Given the depth of water, where fish is located, being ‘h’ and the critical angle for water-air interface being ‘ic’, find out by drawing a suitable ray diagram the relationship between the radius of the cone and the height ‘h’.
Answer.

Question 21. An ordinary moving coil ammeter used in d.c. cannot be used to measure an alternating current even if its frequency is low. Explain why?
Answer.In alternating current, both magnitude and direction of current changes with time, which makes the needle of ordinary moving coil ammeter oscillate even with low frequency of A.C. Hence it can not be used to measure alternating current.
Question 22. State de Broglie hypothesis. Is it applicable for moving electron of hydrogen atom ?
OR
Calculate the de-Broglie wavelength of the electron orbiting in the n = 2 state of hydrogen atom.
Answer.de-Broglie hypothesis : It states that a moving particle sometimes acts as a particle or a wave associated with moving particle which controls the
particle in every respect. The wave associated with moving particle is called matter wave or de-Broglie
wave whose wavelength is given by λ = h/mv where m and v are the mass and velocity of the particle and h is Planck’s constant.
Yes, it is applicable for moving electron of hydrogen atom.
OR
Kinetic energy of the electron in the second state of hydrogen atom

Question 23. How does the angle of dip vary as one moves from the equator towards the north pole? If the horizontal component of earth’s magnetic field at a place where the angle of dip is 60° is 0.4 × 10–4 T, calculate the vertical component and the resultant magnetic field of earth at that point.
Answer.As one moves from the equator towards north pole, angle of dip increases such that north pole of the bar magnet bends downwards.

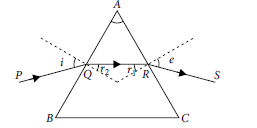
Question 24. Figure shows a ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, show that
(i) r1 = r2 = A/2,
(ii) angle of minimum deviation, Dm = 2i – A.
Answer.

Question 25. When the oscillating electric and magnetic fields are along the x-and y-direction respectively,
(i) point out the direction of propagation of electromagnetic wave.
(ii) express the velocity of propagation in terms of the amplitudes of the oscillating electric and magnetic fields.
(iii) Write the expression of energy density and momentum carried by the electromagnetic waves.
Answer.
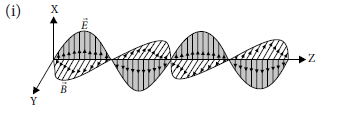
Propagation of electromagnetic wave is along z-axis.
(ii) Speed of electromagnetic wave can be given as the ratio of magnitude of electric field (E0) to the magnitude of magnetic field (B0), i.e., c E0=B0
(iii) Energy density carried by the electromagnetic waves is
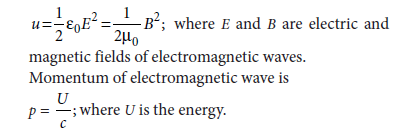
SECTION – D
Question 26. Figure shows two long coaxial solenoids, each of length ‘l’. The outer solenoid has an area of cross-section A1 and number of turns per unit length n1. The corresponding values for the inner solenoid are A2 and n2. Write the expression for self inductance L1, L2 of the two coils and their mutual inductance M. Hence show that
M < √L1L2 .

OR
State Lenz’s law. A metallic rod held horizontally along east-west direction, is allowed to fall under gravity.
Will there be an emf induced at its ends? Justify your answer.
Answer.

OR
Lenz’s law states that the direction of the induced emf and the direction of induced current are such that they oppose the cause which produces them.
The rod held along east west direction will fall in a perpendicular magnetic field BH present in N-S direction. Hence an emf will be induced in the rod following the relation for the motional emf e = BHvl.
Question 27. State working principle of potentiometer. Explain how the balance point shifts when value of resistor R increases in the circuit of potentiometer, given below.

Answer. Principle of potentiometer : When a constant current flows through a wire of uniform area of crosssection, the potential drop across any length of the wire is directly proportional to the length. Let resistance of wire AB be R1 and its length be l then current drawn from driving cell
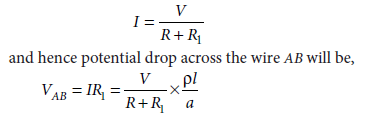
where a is the area of cross-section of the wire AB.
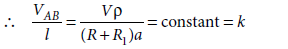
When R increases, current and potential difference across wire AB will be decreased and hence potential gradient k will also be decreased. Thus the null point or balance point will shift to right (towards, B) side.
Question 28. (a) Two slits in Young’s double slit experiment are illuminated by two different lamps emitting light of the same wavelength. Will you observe the interference pattern? Justify your answer.
(b) In Young’s double slit experiment using monochromatic light of wavelength l, the intensity of light at a point on the screen where path difference is l, is K units. Find out the intensity of light at a point where path difference is l/3.
OR
(a) In a single slit diffraction pattern, how does the angular width of the central maximum vary, when
(i) aperture of slit is increased?
(ii) distance between the slit and the screen is decreased?
(b) How is the diffraction pattern different from the interference pattern obtained in Young’s double slit experiment?
Answer.(a) Two different lamps emit light waves which are not coherent, as they are not in same phase or not have stable phase difference. Due to this, no sustained interference pattern can be obtained on screen.


where the letters have their usual meanings.
(i) Effect of slit width : From the equations (i), it follows that β0∝1/a. Therefore, as the slit width is increased, the width of the central maximum will decrease.
(ii) Effect of distance between slit and screen (D) : From the equation (i), it follows that 2q0 is independent of D. So the angular width will remain same whatever the value of D.
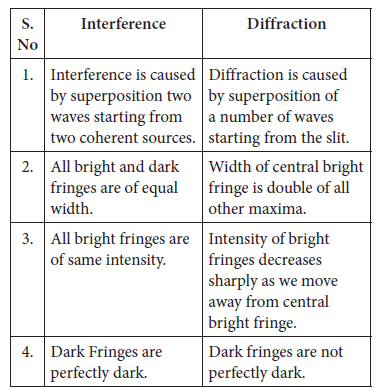
(b) Difference between interference and diffraction Experiment to observe diffraction pattern
Question 29. Two identical spheres A and B, each having a charge of 6 × 10–8C, are separated by 60 cm. A third uncharged sphere C of the same size is brought in contact with sphere A, then brought in contact with sphere B and finally removed from both. What is the new force of repulsion between A and B?
Answer.

Question 30. Suggest an idea to convert a full wave rectifier to a half wave rectifier by changing the connecting wires Draw the diagram and explain your answer.
Answer. Circuit diagram
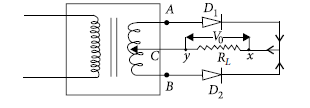
One possible answer: Change the connection of RL from point C to point B.
Now no current flowing through D2 in the second half.
SECTION – E
Question 31. (a) Define magnifying power of a telescope. Write its expression.
(b) A small telescope has an objective lens of focal length 150 cm and an eye piece of focal length 5 cm. If this telescope is used to view a 100 m high tower 3 km away, find the height of the final image when it is formed 25 cm away from the eyepiece.
OR
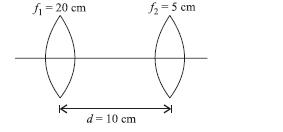
(a) Define power of a lens. Write its units. Deduce the relation 1/f= 1/f1 + 1/f 2 for two thin lenses kept in contact coaxially.
(b) Two converging lens of focal length 20 cm and 5 cm are kept at a distance of 10 cm in air, find the equivalent power of the combination.
Answer.(a) When the final image is formed at least distance of distinct vision :
Magnifying power of refracting telescope (M) is defined as the ratio of the angle subtended by the image (β) at the eye to the angle subtended by the distant object at the unaided eye (α).
M = β/α
We can increase the magnifying power of telescope by
(i) Increasing the focal length of the objective.
(ii) Decreasing the focal length of eyepiece.
(b) Here, fo = 150 cm, fe = 5 cm
Angle subtended by 100 m tall tower at 3 km is



Question 32. Draw the magnetic field lines due to a current passing through a long solenoid. Use Ampere’s circuital law, to obtain the expression for the magnetic field due to the current I in a long solenoid having n number of turns per unit length.
OR
(a) How is a toroid different from a solenoid ?
(b) Use Ampere’s circuital law to obtain the magnetic field inside a toroid.
(c) Show that in an ideal toroid, the magnetic field (i) inside the toroid and (ii) outside the toroid at any point in the open space is zero.
Answer.
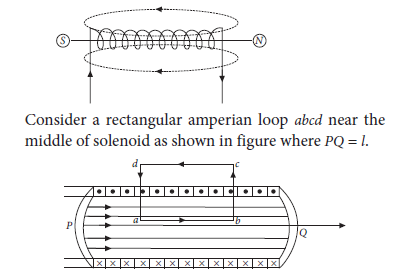
Let the magnetic field along the path ab be B and is zero along cd. As the paths bc and da are perpendicular to the axis of solenoid, the magnetic field component along these paths is zero. Therefore, the path bc and da will not contribute to the line integral of magnetic field B.
Total number of turns in length l = nl
The line integral of magnetic field induction B over the closed path abcd is




Question 33. A slow neutron strikes a nucleus of 92U235 splitting it into lighter nuclei of barium and krypton and releasing three neutrons. Write the corresponding nuclear reaction. Also calculate the energy released in this reaction.
Given that m(92U235) = 235.043933 a.m.u., m(n1) = 1.008665 a.m.u. m(56Ba141) = 140.917700 a.m.u. and m(36(Kr92) = 91.895400 a.m.u.
OR
(a) Why is the binding energy per nucleon found to be constant for nuclei in the range of mass number (A) lying between 30 and 170?
(b) When a heavy nucleus with mass number A = 240 breaks into two nuclei, A = 120, energy is released in the process. Why?
Answer. The nuclear reaction can be represented as

Note : It is not mentioned in the problem as to whether the given masses are atomic masses or nuclear masses.
In case, the given masses are nuclear masses, the solutions is quite simple. The problem has been solved by considering the given masses as atomic masses.
OR
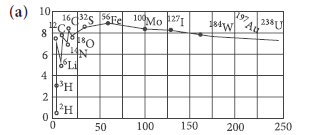
The constancy of binding energy in the range 30 < A < 170 is a consequence of the fact that the nuclear force is short ranged. Consider a particular nucleon inside a sufficiently large nucleus. It will be under the influence of only some of its neighbours, which come within the range of the nuclear force. If any other nucleon is at a distance more than the range of the nuclear force from the particular nucleon it will have no influence on the binding energy of the nucleon under consideration. If a nucleon can have a maximum of p neighbours within the range of nuclear force, its binding energy would be proportional to p. Let the binding energy of the nucleus be pk, where k is a constant having the dimensions of energy. If we increase A by adding nucleons they will not change the binding energy of a nucleon inside. Since most of the nucleons in a large nucleus reside inside it and not on the surface, the change in binding energy per nucleon would be small. The binding energy per nucleon is a constant and is approximately equal to pk.
(b) A very heavy nucleus with A = 240, has lower binding energy per nucleon compared to that of a nucleus with
A = 120. When a heavy nucleus with mass number
A = 240 breaks into two nuclei, A = 120, energy is released in this process.
