CBSE Class 12 Mathematics Sample Paper Set G

See below CBSE Class 12 Mathematics Sample Paper Set G with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.

SECTION A

Question numbers 01 to 20 carry 1 mark each.

1. If f and g are two functions from R to R defined as f (x) = |x| + x and g(x) = |x| − x , then fog (x) for x < 0 is
(a) 4x
(b) 2x
(c) 0
(d) –4x 

2. The principal value of cot⁻¹(−√3) is
(a)−π/6
(b) π/6
(c) 2π/3
(d) 5π/6 

3. 

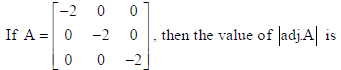
(a) 64
(b) 16
(c) 0
(d) –8 

4. The maximum value of slope of the curve y = −x³ + 3x² +12x −5 is
(a) 15
(b) 12
(c) 9
(d) 0 

5. 

(a) tan(xe^x) + C
(b) cot(xe^x) + C
(c) cot(e^x) + C
(d) tan[e^x (1+ x)]+ C 

6. The degree of the differential equation 

(a) 1
(b) 2
(c) 3
(d) 6 

7. The value of p for which p(î + j+ k̂ ) is a unit vector is
(a) 0
(b) 1/√3
(c) 1
(d) √3 

8. The coordinates of the foot of the perpendicular drawn from the point (–2, 8, 7) on the XZ-plane
is
(a) (–2, –8, 7)
(b) (2, 8, –7)
(c) (–2, 0, 7)
(d) (0, 8, 0)

9. The vector equation of XY-plane is
(a) r̅.k̂ = 0
(b) r̅.ĵ = 0
(c) r̅.î = 0
(d) r̅.n̅ =1 

10. The feasible region for an LPP is shown below :

Let z = 3x − 4y be the objective function. Minimum of z occurs at
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10) 

11. If y = tan⁻¹ x + cot⁻¹ x, x ∈ R , then dy/dx is equal to _______.
Sol. We have y = tan⁻¹ x + cot⁻¹ x, x ∈ R
⇒ y = π/2
∴ dy/dx = 0

OR

If cos(xy) = k , where k is a constant and xy ≠ nπ, n ∈ Z , then dy/dx is equal to ______.
Sol.

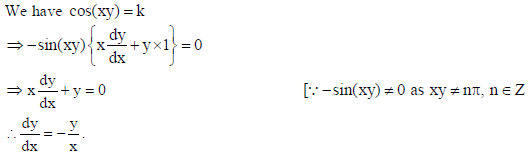
12. The value of λ so that the function f defined by

is continuous at x = π is ___________.
Sol. As f is continuous at x = π so, lim_x→π+ f(x) = lim_x→π- f(x) = f(π)
Now consider lim_x→π+ f(x) = f(π)
⇒ lim_x→π+ cos x = (λ)π
⇒ cos π = λ(π)
∴ λ = − 1/π.

13. The equation of the tangent to the curve y = sec x at the point (0, 1) is ________.
Sol. Here dy/dx = sec x tan x
Slope of tangent at (0, 1) is sec 0 tan 0 =1×0 = 0 .
So, equation of tangent : y −1= 0(x − 0)              ∴ y =1.

14. The area of the parallelogram whose diagonals are 2î and −3k̂ is ______ square units.
Sol. Required area of parallelogram = 1/2|2î × (−3k̂)| = 1/2|6ĵ| = 1/2 × 6 = 3 square units 

OR

The value of λ for which the vectors 2î, − λĵ+ k̂ and î + 2ĵ− k̂ are orthogonal is ______.
Sol. As 2î, − λĵ+ k̂ and î + 2ĵ− k̂ are orthogonal so, (2î − λĵ+ k̂ ).(î + 2ĵ− k̂ ) = 0
⇒ 2 − 2λ −1 = 0
∴ λ = 1/2

15. A bag contains 3 black, 4 red and 2 green balls. If three balls are drawn simultaneously at random, then the probability that the balls are of different colours is ________.
Sol. 

Question numbers 16 to 20 are of very short answer type questions.

16. Construct a 2× 2 matrix ij A = [a_ij] whose elements are given by a_ij = |(i)² − j| .
Sol.

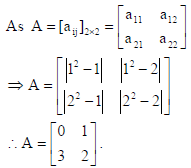
17. Differentiate sin² (√x) with respect to x.
Sol.

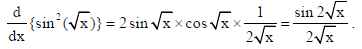
18. Find the interval in which the function f given by f (x) = 7 − 4x − x² is strictly increasing.
Sol. We have f (x) = 7 − 4x − x²
⇒ f ‘(x) = −4 − 2x
For f ‘(x) = −4 − 2x = 0                  ⇒ x = −2
In x∈(−∞,−2), f ‘(x) > 0 so, f (x) is strictly increasing in x∈(−∞,−2) .

19. Evaluate :

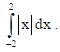
Sol.

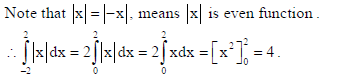
OR

Find : ∫ dx/9 + 4x².
Sol. 

20. An unbiased coin is tossed 4 times. Find the probability of getting at least one head.
Sol. P(at least one head) =1− P(no head) =1− P(all tails)   

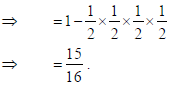
SECTION B

Question numbers 21 to 26 carry 2 marks each.

21. Solve for x : sin⁻¹ 4x sin⁻¹ 3x = − π/2.
Sol.

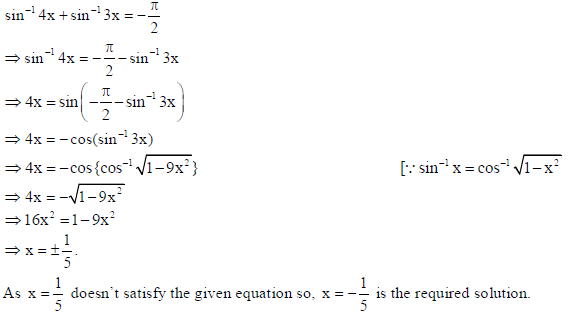
OR

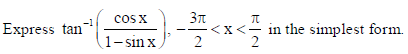
Sol.

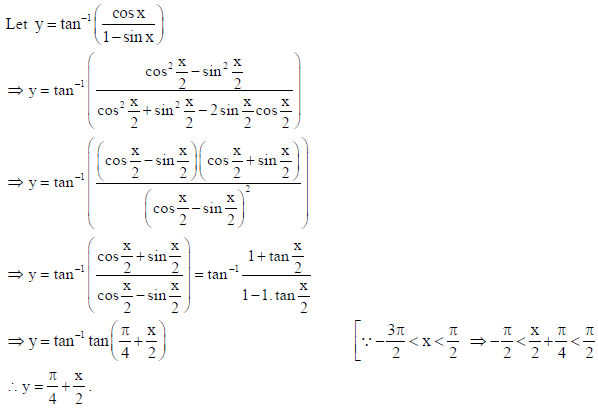
22.

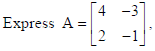
as sum of a symmetric and a skew symmetric matrix.
Sol. 

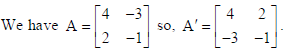
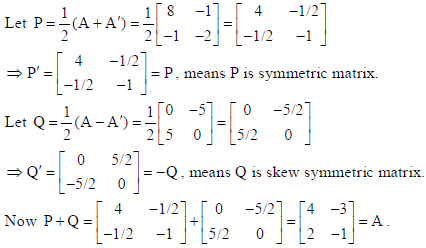
23. If y² cos(1/x) = a², then find dy/dx.
Sol.

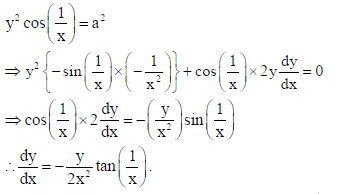
24. Show that for any two non-zero vectors a̅ and b̅
|a̅| + |b̅| = |a̅| − |b̅| iff  a̅ and b̅ are perpendicular vectors.
Sol. We ha̅ve |a̅ + b̅| = |a̅ − b̅|
⇒ |a̅ + b̅|² = |a̅ − b̅|²
⇒ (a̅ + b̅).(a̅ + b̅) = (a̅ − b̅).(a̅ − b̅)
⇒ |a̅|² + |b̅|² + 2a̅.b̅ = |a̅|² + |b̅|² − 2a̅.b̅
⇒ 4a̅.b̅ = 0
⇒ a̅.b̅ = 0
As a̅ a̅nd b̅ are non-zero vectors, so a̅ ⊥ b̅.

OR

Show that the vectors 2î, − ĵ+ k̂, 3î + 7ĵ+ k̂ and 5î, + 6ĵ+ 2k̂ form the sides of a right-angled
triangle.
Sol. 

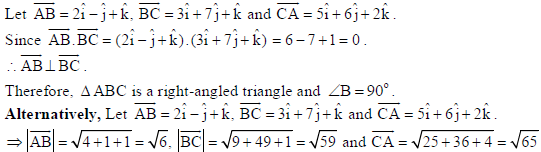
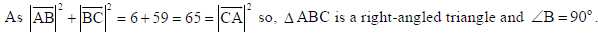
25. Find the coordinates of the point where the line through (–1, 1, –8) and (5, –2, 10) crosses the ZX-plane.
Sol. Equation of line passing through the given points : 

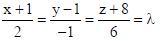
Note that the d.r.’s of this line are 6, –3, 18 i.e., 2, –1, 6.
Coordinates of any random point on this line : A(2λ −1,−λ +1,6λ −8) .
If this line crosses ZX-plane then, we must have −λ +1 = 0 ⇒ λ =1          [Eq. of ZX-plane : y = 0
Therefore the required coordinates of the point : A(1, 0, –2).

26. If A and B are two events such that P(A) = 0.4, P(B) = 0.3 and P(A∪B) = 0.6 , then find P(B’∩ A) .
Sol. Note that, P(A∩B) = P(A) + P(B) − P(A∪B)
⇒ P(A∩B) = 0.4 + 0.3− 0.6 = 0.1 
Now P(B’∩A) = P(A−B) = P(A) − P(A∩B)
⇒ = 0.4 − 0.1
⇒ = 0.3.

SECTION C

Question numbers 27 to 32 carry 4 marks each.

27. Show that the function f : (−∞,0)→(−1,0) defined by f (x) = x/1+|x|, x∈ (−∞,0) is one-one and onto.
Sol. Here f : (−∞,0)→(−1,0) is defined by f (x) = x/1+|x|, x ∈ (−∞ ,0)
One-one : Let x₁ , x₂ ∈ (−∞,0) so that 1 2 f (x₁) = f (x₂)
⇒ x₁/ 1+|x₁| = x₂ / 1+|x₂|
Cleary, x₁ , x₂ <0 therefore, x₁/ 1−x₁ = x₂ / 1−x₂
⇒ x₁ − x₁ x₂ = x₂ − x₁ x₂ 
⇒ x₁ = x₂
So, f is one-one.
Onto : Let y∈ (−1,0) so that y = f (x)
⇒ y = x/ 1+|x|
⇒ y = x/ 1±x
⇒ x = y/ 1±y ∈ (−∞,0 for all −1 < y < 0
So, f is onto function.

OR

Show that the relation R in the set A = {1, 2,3, 4,5,6} given by
R = {(a, b) : |a − b| is divisible by 2} is an equivalence relation.
Sol. Here R = {(a, b) : |a − b| is divisible by 2} is defined on set A.
Reflexivity : As a − a = 0 is divisible by 2 ∀ a ∈ A.
∴(a,a) ∈ R .
Therefore, R is reflexive.
Symmetry : Let (a,b)∈R for all a,b ∈ A. It implies a − b is divisible by 2 .
This further implies, b − a is also divisible by 2.
So, (b,a) ∈ R .
Therefore, R is symmetric.
Transitivity : Let (a,b)∈R and (b,c) ∈ R ∀ a,b,c ∈ A.
It implies a − b is divisible by 2 and b − c is divisible by 2 .
This further implies, (a − b) + (b − c) = a − c is also divisible by 2 .
So, (a,c) ∈ R .
Therefore, R is transitive.
Hence, R is an equivalence relation.

28. If y = x³ (cos x)^x + sin⁻¹ √x , find dy/dx.
Sol.

29. Evaluate :

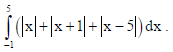
Sol.

30. Find the general solution of the differential equation
       x²ydx − (x³ + y³ )dy = 0.
Sol. 

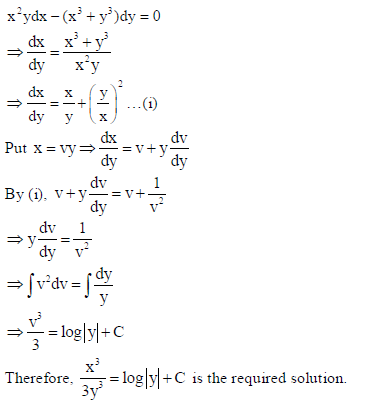
31. Solve the following LPP graphically :
Minimise z = 5x + 7y
subject to the constraints
2x + y ≥ 8,
x + 2y ≥ 10,
x, y ≥ 0.
Sol.

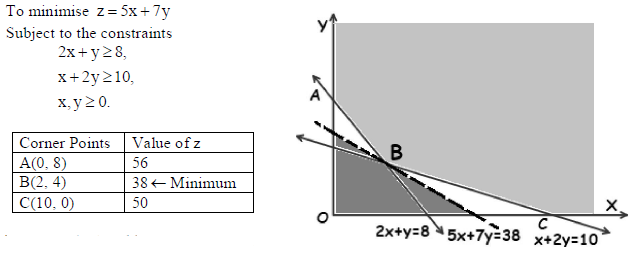
Note that the feasible region is unbounded.
So z = 38 may or may not be the minimum value.
To check, let 5x + 7y < 38 .
Since the feasible region and 5x + 7y < 38 doesn’t have any common point.
Therefore, z = 38 is the minimum value of z.

32. A bag contains two coins, one biased and the other unbiased. When tossed, the biased coin has a 60% chance of showing heads. One of the coins is selected at random and on tossing it shows tail. What is the probability it was an unbiased coin?
Sol. Let E : the coin shows tail, E₁ : a biased coin is selected and E₂ : an unbiased coin is selected.
Here P(E₁)=  1/2, P(E₂) = 1/2, P(E | E₁ ) = 40%, P(E | E₂ ) = 50%
Note that the biased coin has a 60% chance of showing heads means, it has 40% chance of showing tails. Also unbiased coin will have 50% chance of showing head and tail each.   

OR

The probability distribution of a random variable X, where k is a constant, is given below :

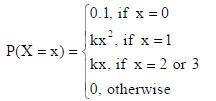
Determine
(a) the value of k
(b) P(X ≤ 2)
(c) Mean of the variable X.
Sol. (a) As ∑ P(X) =1
∴ P(0) + P(1) + P(2) + P(3) + P(4) +… =1
⇒ 0.1+ k(1)² + k(2) + k(3) + 0 +… =1
⇒ 6k = 0.9
⇒ k = 3/20 .
(b) P(X ≤ 2) = P(0) + P(1) + P(2)
⇒ P(X ≤ 2) = 0.1 + k + 2k = 1/10 + 3 × 3/20
∴  P(X ≤ 2) = 11/20.
(c) Mean, μ =∑XP(X)
⇒ μ = 0.P(0) +1.P(1) + 2.P(2) + 3.P(3) + 4.P(4) +…
⇒ μ = 0 ×(0.1) +1×(k) + 2×(2k) + 3×(3k) + 4×(0) +…
⇒ μ =14k
⇒ μ = 14 × 3/20
∴ Mean = 2.1.

SECTION D

Question numbers 33 to 36 carry 6 marks each.

33. Solve the following system of equations by matrix method :
                  x − y + 2z = 7 ,
                2x − y + 3z =12 ,
                3x + 2y − z = 5 .
Sol.

OR

Obtain the inverse of the following matrix using elementary operations :

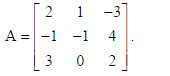
Sol.

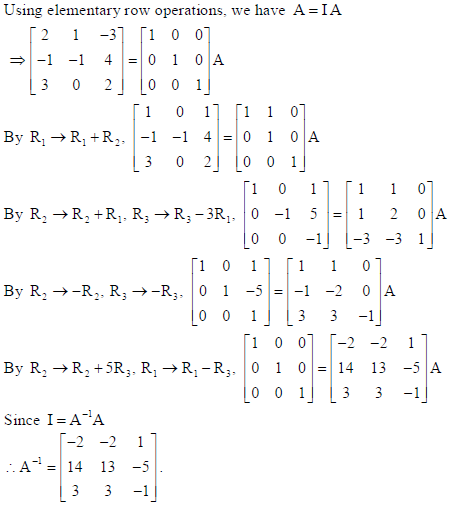
34. Find the point on the curve 9y² = x³ , where the normal to the curve makes equal intercepts with both the axes. Also find the equation of the normals.
Sol. We have 9y² = x³ .
Let the required point be P(α,β) .
So, 9β² = α³…(i)

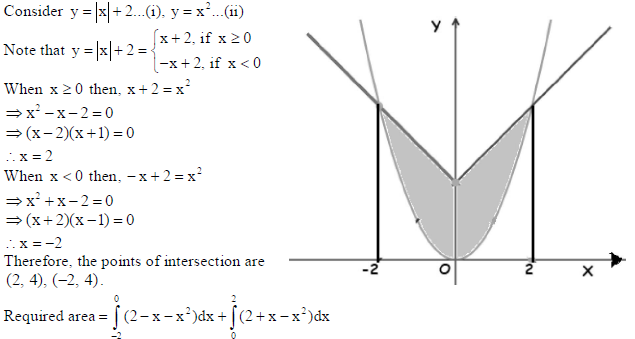
35. Find the area of the following region using integration :
{(x, y) : y ≤ |x| + 2, y ≥ x²} .
Sol.

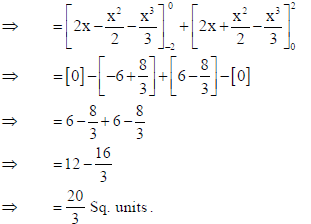
OR

Using integration, find the area of a triangle whose vertices are (1, 0), (2, 2) and (3, 1).
Sol.

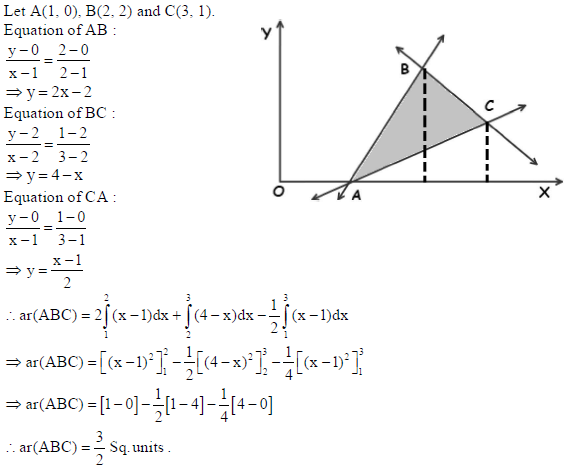
36

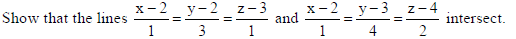
Also, find the coordinates of the point of intersection. Find the equation of the plane containing
the two lines.
Sol.

The coordinates of random points on these lines are given as, A(λ + 2, 3λ + 2, λ + 3) and
B(μ + 2, 4μ + 3, 2μ + 4) respectively.
If lines intersect then A and B must coincide that means,
λ + 2 = μ + 2, 3λ + 2 = 4μ + 3, λ + 3 = 2μ + 4
⇒ λ = μ…(i)
3λ − 4μ =1…(ii)
λ − 2μ =1…(iii)
Solving (i) and (ii), we get : λ = −1, μ = −1.
Putting λ = −1, μ = −1 in LHS of (iii) : λ − 2μ = −1− 2(−1) =1= RHS of (iii) .
Hence A and B will coincide and therefore, the lines L₁ and L₂ will intersect.
Also the point of intersection will be (1, –1, 2).
Now we have three points on the plane which contains these lines i.e., (2, 2, 3), (2, 3, 4) and (1,
–1, 2).
So, equation of plane containing the two lines :

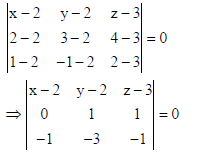
Expanding along R₁, we get : 2(x − 2) − (y − 2) + (z − 3) = 0
⇒ 2x − y + z −5 = 0 .