Please refer to Case Study Chapter 8 Trigonometry Mathematics with answers provided below. These case study based questions are expected to come in the upcoming Class 10 Mathematics examinations. We have provided case study questions class 10 maths for all chapters on our website as per the latest examination pattern issued by CBSE, NCERT, and KVS.
Chapter 8 Trigonometry Case study Questions Class 10 Maths
I. Three children were playing with sticks. As they had one stick each of them, they put all the three sticks together. Finding all the three sticks equal, they pick up the sticks and put them in a triangular form in such a way that the ends of each stick touch the other. They were surprised. Now they thought of a plane. They took another stick and put it as in the adjacent figure. The stick AD is just touching the stick BC. Somehow, they measured each angle. Finding that each angle. ∠A = ∠B = ∠C = 60° (equal) and ∠BAD = ∠CAD = 30°. Likewise, they measured BD = CD, and ∠ADB = ∠ADC = 90°. Taking AB = BC = CA = 2a, you are required to answer the following questions:
Question. Using the above figure, the value of cos 60° is
(a) 0
(b) 1
(c) 1 2
(d) √3 /2
Answer
C
Question. Using the above figure, the value of tan 30° is
(a) √3
(b) 1
(c) 0
(d) 1/√3
Answer
D
Question. Using the above figure, the value of cosec 60° is
(a) 2/√3
(b) √3/2
(c) 1/ 2
(d) 1/√2
Answer
A
Question. The length of AD is
(a) a
(b) 2a
(c) 2a
(d) 3a
Answer
D
Question. Using the above figure, the value of sin 30° is
(a) 1/ 2
(b) 1/√2
(c) √3/2
(d) 1
Answer
A
II. Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of anything between 100 metres to 300 metres. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be raised properly and effectively.
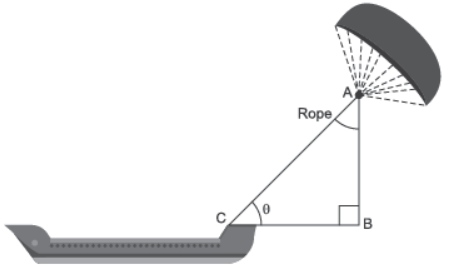
Question. If BC = 15 m, q = 30°, then AB is
(a) 2 √3 m
(b) 15 m
(c) 24 m
(d) 5 3 m
Answer
D
Question. What should be the length of the rope of the kite sail in order to pull the ship at the angle q (calculated in part (a) and be at a vertical height of 200 m?
(a) 300 m
(b) 400 m
(c) 500 m
(d) 600 m
Answer
B
Question. Suppose AB = BC = 12 m, then q =
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Answer
C
Question. Given that BC = 6 m and q = 45°. The values of AB and AC are respectively
(a) AB = 4 m, AC = 4 √2 m
(b) AB = 7 m, AC = 7 √5 m
(c) AB = 9 m, AC = 9 √3 m
(d) AB = 6 m, AC = 6 √2 m
Answer
D
Question. In the given figures, if sin q = cos (3q – 30°), where q and 3q – 30° are acute angles, then the value of q is
(a) 30°
(b) 60°
(c) 45°
(d) None of these.
Answer
A
We hope you liked the above provided Case Study Chapter 8 Trigonometry Mathematics case study questions class 10 maths provided above. Please let us know in the comments box below if you have any questions.


