Assignments Class 10 Mathematics Real Numbers

Please refer to Assignments Class 10 Mathematics Real Numbers Chapter 1 with solved questions and answers. We have provided Class 10 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 1 Real Numbers Class 10 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.

Real Numbers Assignments Class 10 Mathematics

VERY SHORT ANSWER TYPE QUESTIONS

Question. The numbers 525 and 3000 are divisible by 3, 5, 15, 25 and 75. What is the HCF of 525 and 3000?
Ans. 75

Question. What is x : y in the factor-tree?

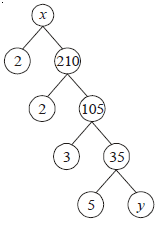
Ans. 60 : 1

Question. Write the prime factof of 2 × 7 × 11 × 13 × 17 + 21
Ans. 7

Question. Find the least number which is divisible by all numbers from 1 to 10 (both inclusive).
Ans. 2520

Question. What can you say about the product of a non-zero rational and irrational number?
Ans. Irrational

Question. pⁿ = (a × 5)ⁿ For pⁿ to end with the digit zero a = _____ for natural number n.
(a) any natural number
(b) even number
(b) odd number
(d) none of these
Ans. (b) even number

Question. HCF is always
(a) multiple of LCM
(b) Factor of LCM
(c) divisible by LCM
(d) (a) and (c) both
Ans. (b) Factor of LCM

Question. After how many places the decimal expansion of 13497/1250 will terminate?
Ans. 4

Question. The decimal expansion of the rational number 327/(2³x5) will terminate after
(a) One decimal place
(b) Two decimal place
(c) Three decimal place
(d) More than three decimal place
Ans. (c) Three decimal place

Question. Which of the following rational numbers have terminating decimal?
(i) 18/225
(ii) 5/18
(iii) 2/21
(iv) 7/250
(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (i) and (iv)
Ans. (d) (i) and (iv)

SHORT ANSWER TYPE QUESTIONS-I

Question. Show that any positive odd integer is of the form 4q + 1 or 4q + 3, where q is some integer.
Ans. By applying Euclid division algorithm to a and b such that a = 4q + r, where b = 4, Now r = 0, 1, 2, 3.
where, r = 0, a = 4q which is even number.
where, r = 1, a = 4q + 1 an odd number.
where, r = 2, a = 4q + 2 =2 (2q + 1), an even number.
where, r = 3, a = 4q + 3 an odd number.

Question. Two tankers contain 850 litres and 680 litres of petrol respectively. Find the maximum capacity of a container which can measure the petrol of either tanker in exact number of times.
Ans. HCF of 850 and 680 is 2 × 5 × 17 = 170 litres.

Question. Find the value of : (–1)ⁿ + (–1)²ⁿ + (–1)²ⁿ⁺¹ + (–1)⁴ⁿ⁺², where n is any positive odd integer.
Ans. Given that n is a positive odd integer
⇒ 2n and 4n + 2 are even positive integers and n and 2n + 1 are odd positive integers.
∴ (–1)ⁿ = – 1, (–1)²ⁿ = + 1, (–1)²ⁿ⁺¹ = – 1, (–1)²ⁿ⁺² = + 1
∴ (–1)ⁿ + (–1)²ⁿ + (–1)²ⁿ⁺¹ + (–1)⁴ⁿ⁺² = – 1 + 1 – 1 + 1 = 0

Question. Show that 12ⁿ cannot end with the digit 0 or 5 for any natural number n.
Ans. As 12 has factors 2, 2, 3 it doesnot has 5 as its factor so 12ⁿ will never end with 0 or 5.

Question. Without actually performing the long division, find if 395/10500 will have terminating or non terminating (repeating decimal expansion.)
Ans. Non-terminating repeating.

SHORT ANSWER TYPE QUESTIONS-II

Question. If the HCF of 1032 and 408 is expressible in the form 1032 p – 408×5, find p.
Ans. p = 2

Question. The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one of the number is 280. Find the other number.
Ans. HCF = 40, LCM = 560
∴ Other No. = 80.

Question. Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of two given number.
Ans. HCF (404, 96) = 4
LCM (404, 96) = 9696
HCF × LCM = 38, 784
Also, 404 × 96 = 38,784

Question. Find the HCF of 56, 96, 324 by Euclid’s algorithm.
Ans. 4

Question. Find the HCF of 180, 252 and 324 by Euclid’s Division algorithm.
Ans. HCF (324, 252, 180) = 36

Question. Find the greatest number of six digits exactly divisible by 18, 24 and 36.
Ans. LCM of (18, 24, 36) = 72.
Greatest six digit number = 999999

Question. Show that any positive odd integer is of the form 6q + 1, 6q + 3 or 6q + 5, where q is some integer.
Ans. Let a be +ve odd integer.
⇒ a = 6q + r where r = 0, 1, 2, 3, 4, 5
If, a = 6q + 0 = 2(3q) is an even integer so not possible
If, a = 6q + 1 is an odd integer
If, a = 6q + 2 = 2(3q + 1) is an even integer so not possible
If, a = 6q + 3 is an odd integer
If, a = 6q + 4 = 2(3q + 2) is an even integer so not possible
If, a = 6q + 5 is an odd integer.

Question. Aakriti decided to distribute milk in an orphanage on her birthday. The supplier brought two milk containers which contain 398ℓ and 436ℓ of milk. The milk is to be transferred to another containers so that 7ℓ and 11ℓ of milk is left in both the containers respectively. What will be the maximum capacity of the drum?
Ans. 17

Question. Prove that 5 – (3/7)√3 is an irrational number.
Ans. 5 is rational no. and (3/7)√3 is an irrational number. Difference of a rational number and irrational number is an irrational number.

Question. Find HCF and LCM of 56 and 112 by prime factorization method.
Ans. HCF : 56, LCM : 112

Question. Find the smallest number, which when increased by 17, is exactly divisible by both 520 and 468.
Ans. 4663
LCM of (468, 520) = 4680
∴ Required no. = 4680 – 17 = 4663

Question. A street shopkeeper prepares 396 Gulab jamuns and 342 ras-gullas. He packs them, in combination. Each containter consists of either gulab jamuns or rasgullab but have equal number of pieces.
Find the number of pieces he should put in each box so that number of boxes are least. How many boxes will be packed in all.
Ans. HCF (396, 342) = 18
No. of boxes = (396 + 342)/18 = 738/18 = 41

Question. Find the number nearest to 110000 but greater than 1 lakh, which is exactly divisible by 8, 15, 21.
Ans. 109200

Question. Find the smallest number which when increased by 20 is exactly divisible by 90 and 144. If we express the smallest number, the LCM, in the form 144 m + 90n, then what are the values of m and n? Is LCM, a multiple of 144?
Ans. [The LCM of (90, 144) – 20] = Required No.
⇒ Required No. = 700
If 720 = 144m + 90n then m = 5, n = 0, Yes

Question. Prove that the product of three consecutive positive integers is divisible by 6.
Ans. Let the three consecutive integers be a, a+1, a + 2,
Case I : If a is even,
⇒ a + 2 is the also even
a(a + 2) is divisible by 2
a(a + 2) (a + 1) is also divisible by 2
Now a, a + 1, a + 2 are three consecutive numbers
⇒ a (a + 1) (a + 2) is a multiple by 3
⇒ a (a + 1) (a + 2) is divisible by 3
as it is divisible by 2 and 3 hence divisible by 6.
Case II : If a is odd
⇒ a + 1 is even
⇒ a + 1 is divisible by 2
⇒ a(a + 1) (a + 2) is also divisible by 2
Again a, a + 1, a + 2 are three consecutive numbers
⇒ a (a + 1) (a + 2) is a multiple by 3
⇒ a (a + 1) (a + 2) is divisible by 3
as it is divisible by 2 and 3 hence divisible by 6.

Question. For any positive integer n, prove that n³–n is divisible by 6.
Ans. n³ – n = n(n² – 1) = n (n – 1) (n + 1)
= (n – 1) (n) (n + 1)
= Product of three consecutive +ve integers
Now to show that produce of three consecutive +ve integers is divisible by 6.
Any +ve integer a is of the form 3q, 3q + 1 or 3q + 2 for some integer q.
Let a, a + 1, a + 2 be any three consecutive integers.
Case I : a = 3q
(3q) (3q + 1) (3q + 2) = 3q (2m) [as (3q + 1) and (3q + 2) are consecutive integers so their product is also even]
= 6q m
which is divisible by 6.
Case II : If a = 3q + 1
a (a + 1) (a + 2) = (3q + 1) (3q + 2) (3q + 3)
= 2m3(q + 1) (as (3q + 1) (3q + 2) = 2m)
= 6 m (q + 1)
which is divisible by 6.
Case III : If a = 3q + 2
a (a + 1) (a + 2) = (3q + 2) (3q + 3) (3q + 4)
= (3q + 2) 3(q + 1) (3q + 4)
= 6 m
which is divisible by 6.