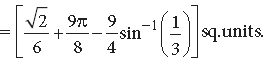Please refer to Application of Integrals Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Mathematics Important Questions Application of Integrals
Short Answer Type Questions
Question. Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32.
Answer. We have curves,
y = x …(i)
and x2 + y2 = 32 …(ii)
Curves (i) and (ii) intersect at (4, 4)
The region enclosed by y = x, x2 + y2 = 32 and x-axis in the first quadrant is shown below:

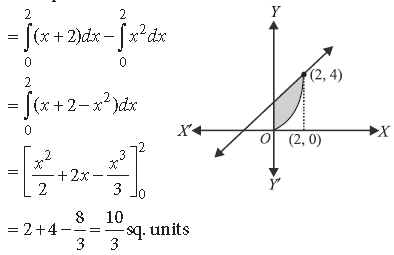
Question. Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = √y and y – axis.
Answer. We have curves x – y + 2 = 0 and x = √y .
x = √y ⇒ y = x2, which is a parabola with vertex at origin.
From the given equations, we get
x – x2 + 2 = 0 ⇒ (x – 2 )(x + 1) = 0
⇒ x = 2 or x = –1
⇒ x = 2 [∵ x ≠ – 1, x is positive]
When x = 2, y = 4
So, the point of intersection is (2, 4)
∴ Required area
Question. Find the area of the region in the first quadrant enclosed by the y-axis, the line y = x and the circle x2 + y2 = 32, using integration.
Answer. The given equation of the circle is x2 + y2 = 32 and the line is y = x
These intersect at A(4, 4) in the first quadrant. The required area is shown shaded in the figure. Points B(0, 4) and C(0,4 √2)

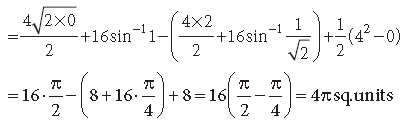
Question. Using integration, find the area of the region bounded by the triangle whose vertices are (– 1, 2), (1, 5) and (3, 4).
Answer. Let A (–1, 2), B (1, 5) and C (3, 4)
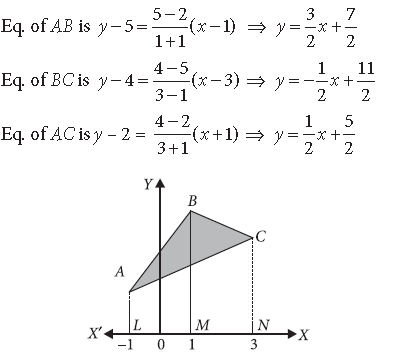
Area of the reqd. triangular region, ABC = Area of trap. ALMB + Area of trap. BMNC – Area of trap. ALNC

Question. Using the method of integration, find the area of the region bounded by the lines : 3x – 2y + 1 = 0, 2x + 3y – 21 = 0 and x – 5y + 9 = 0.
Answer. The given lines are
3x – 2y + 1 = 0 …(i), 2x + 3y – 21 = 0 …(ii) and x – 5y + 9 = 0 …(iii)
Solving (i) and (ii), we get x =3, y = 5
Solving (ii) and (iii), we get x =6, y = 3
Solving (i) and (iii), we get x =1, y = 2

Question. Find the area of the region {(x, y) : x2 + y2 ≤, 4 x + y ≥ 2}
Answer. The given curves are
x2 + y2 = 4 …(i) and x + y = 2 …(ii)


Question. Draw the graph of y = |x + 1|and using integration, find the area below y = |x + 1|, above x – axis and between x = – 4 to x = 2.
Answer.

Thus we get two lines –x + y = 1 …(i), x + y = –1 …(ii)
Their graphs are as shown and the area to be calculated is shaded.

Question. Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Answer. We have, y2 = x and x + y = 2
Solving these two equations, we get y2 + y – 2 = 0
⇒ (y + 2)(y – 1) = 0 ⇒ y = – 2, 1
When y = – 2, x = 4 and when y = 1, x = 1

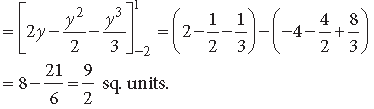
Question. Using integration, find the area of the triangle ABC where A is (2, 3), B is (4, 7) and C is (6, 2).
Answer. Here A (2, 3), B (4, 7) and C (6, 2)


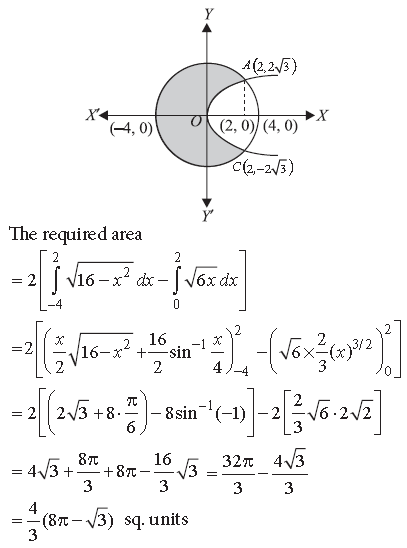
Question. Using integration, find the area of the circle x2 + y2 = 16, which is exterior to the parabola y2 = 6x.
Answer. We have y2 = 6x which is a parabola and
x2 + y2 = 16 which is a circle with centre at (0, 0) and radius 4.
Solving both, we get x2 + 6x – 16 = 0
⇒ (x + 8)(x – 2) = 0
⇒ x = 2 (∵ x = – 8 is not possible)
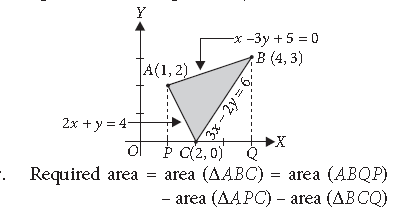
Question. Using the method of integration, find the area of the region bounded by the lines 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0.
Answer. The given lines are 2x + y = 4 …(i)
3x – 2y = 6 …(ii) and x – 3y + 5 = 0 …(iii)
Solving (i) and (ii), we get x = 2, y = 0
Solving (ii) and (iii), we get x = 4, y = 3
Solving (i) and (iii), we get x = 1, y = 2

Question. Find the area of the smaller region bounded by
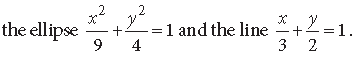
Answer.
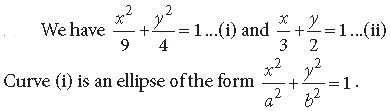
That means its major axis is along x – axis. Also this ellipse is symmetrical about the x – axis.

Long Answer Type Questions
Question. Using integration find the area of the region {(x, y) : x2 + y2 ≤ 2ax, y2 ≥ ax; x, y ≥ 0}
Answer. Let R = {(x, y) : x2 + y2 ≤ 2ax, y2 ≥ ax ; x, y ≥ 0}
⇒ R = R1 ∩ R2 ∩ R3
where R1 = {(x, y) : x2 + y2 ≤ 2ax},
R2 = {(x, y) : y2 ≥ ax} and R3 = {(x, y) : x ≥ 0, y ≥ 0}
Region R1 : (x – a)2 + y2 = a2 represents a circle with centre at (a, 0 ) and radius a.
Region R2 : y2 = ax represents a parabola with vertex at (0, 0) and its axis along x-axis.
Region R3 : x ≥ 0, y ≥ 0 represents the first quadrant.
⇒ R = R1 ∩ R2 ∩ R3 is the shaded portion in the figure.
Since, given curves are x2 + y2 = 2ax and y2 = ax
So, point of intersection of the curves are (0, 0) and (a, a).

Question. Find the area of the region {(x, y) : y2 ≤ 6ax and x2 + y2 ≤ 16a2} using method of integration.
Answer. Let R = { (x, y) : y2 ≤ 6 ax and x2 + y2 ≤ 16 a2}
Let us draw the curves
y2 = 6ax …(i) and x2+ y2 = 16a2 …(ii)

From (i) and (ii),
x2 + 6ax = 16 a2 ⇒ (x + 8a) (x – 2a) = 0 ⇒ x = 2a
(Note : x ≠ – 8a as curve (i) lies in 1st and 4th quadrants only).
Curves intersect at point
B (2a, 2 √3a ) and C (2a, – 2 √3a )
Now in view of symmetry, the required area

Question. Find the area of the region {(x, y) : y2 ≤ 4x, 4x2 + 4y2 ≤ 9}, using integration.
Answer. Let R = {(x, y) : y2 ≤ 4x, 4x2+ 4y2 ≤ 9}
= {(x, y): y2 ≤ 4x }∩ (x, y) : 4x2 + 4y2 ≤ 9 } = R1 ∩ R2.
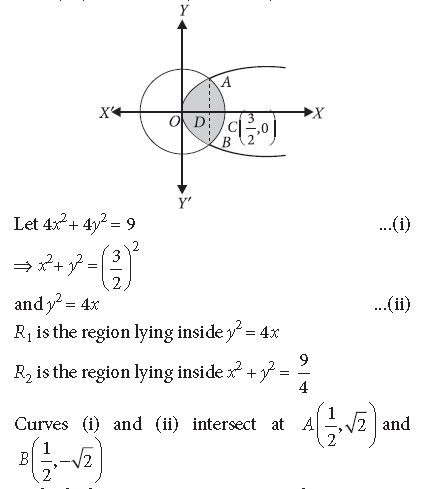
As both the curves are symmteric. about x – axis.
∴ Reqd. area = 2 (Area of the shaded region above
x – axis) = 2 (Area OADO + ADCA)