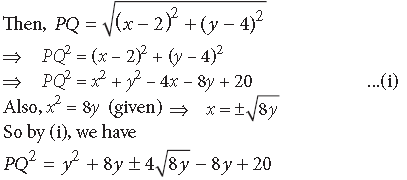Please refer to Application of Derivatives Class 12 Mathematics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Mathematics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Mathematics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Mathematics Important Questions Application of Derivatives
Question. If the function f given by f(x) = x3 – 3(a – 2)x2 + 3ax + 7, for some a∈R is increasing in (0, 1] and decreasing in [1, 5), then a root of the equation, ( f(x) − 14) / (x − 1)2 = (x ≠ 1) is
(a) –7
(b) 5
(c) 7
(d) 6
Question. Let
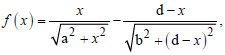
x ∈ R where a, b and d are non-zero real constants. Then :
(a) f is an increasing function of x
(b) f is a decreasing function of x
(c) f’ is not a continuous function of x
(d) f is neither increasing nor decreasing function of x
Question. The tangent at the point (2, –2) to the curve, x2y2 – 2x = 4 (1–y) does not pass through the point :
(a) (4, 1/3)
(b) (8, 5)
(c) (–4, –9)
(d) (–2, –7)
Question. Consider
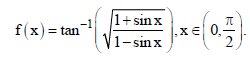
normal to y = f(x) at x = π/6 also passes through the point:
(a) (π/6, 0)
(a) (π/4, 0)
(c) (0, 0)
(d) (0, 2π/3)
Question. If f(x) = xex(1 – x), x ∈ R , then f(x) is
(a) decreasing on [–1/2, 1]
(b) decreasing on R
(c) increasing on [–1/2, 1]
(d) increasing on R
Question. Angle between the tangents to the curve y = x2 – 5x + 6 at the points (2, 0) and (3, 0) is
(a) π
(b) π/2
(c) π/6
(d) π/4
Question. The normal to the curve x = a (cos θ + θ sin θ ), y = a (sin θ – θ cos θ ) at any point θ is such that
(a) it passes through the origin
(b) it makes an angle π/2 + θ with the x- axis
(c) it passes through (a + π/2, −a)
(d) It is at a constant distance from the origin
Question. For real x, let f (x) = x3 + 5x + 1, then
(a) f is onto R but not one-one
(b) f is one-one and onto R
(c) f is neither one-one nor onto R
(d) f is one-one but not onto R
Question. If b is one of the angles between the normals to the ellipse, x2 + 3y2 = 9 at the points (3cosθ, √3 sinθ) and (– 3sin θ, √3cos θ); ∈ (0, π/2); then (2 cotβ)/(sin 2θ) is equal to
(a) √2
(b) 2/√3
(c) 1/√3
(d) √3/4
Question. A normal to the hyperbola, 4x2 – 9y2 = 36 meets the coordinate axes x and y at A and B, respectively. If the parallelogram OABP (O being the origin) is formed, then the locus of P is
(a) 4x2 – 9y2 = 121
(b) 4x2 + 9y2 = 121
(c) 9x2 – 4y2 = 169
(d) 9x2 + 4y2 = 169
Question. A 2 m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate 25 cm/sec., then the rate (in cm/sec.) at which the bottom of the ladder slides away from the wall on the hori ontal ground when the top of the ladder is 1 m above the ground is:
(a) 25√3
(b) 25/√3
(c) 25/3
(d) 25
Question. If the volume of a spherical ball is increasing at the rate of 4π cc/sec, then the rate of increase of its radius (in cm/sec), when the volume is 288 π cc,
(a) 1/6
(b) 1/9
(c) 1/36
(d) 1/24
Question. The maximum area (in sq. units) of a rectangle having its base on the x-axis and its other two vertices on the parabola, y = 12 – x2 such that the rectangle lies inside the parabola, is:
(a) 36
(b) 20√2
(c) 32
(d) 18√3
Question. The tangent to the curve y = x2 – 5x + 5, parallel to the line 2y = 4x + 1, also passes through the point :
(a) (7/2, 1/4)
(b) (1/8, -7)
(c) (- 1/8, 7)
(d) (1/4, 7/2)
Question. If the surface area of a sphere of radius r is increasing uniformly at the rate 8 cm2/s, then the rate of change of its volume is :
(a) constant
(b) proportional to √r
(c) proportional to r2
(d) proportional to r
Question. The weight W of a certain stock of fish is given by W = nw, where n is the si e of stock and w is the average weight of a fish. If n and w change with time t as n = 2t2 + 3 and w = t2 – t + 2, then the rate of change of W with respect to t at t = 1 is
(a) 1
(b) 8
(c) 13
(d) 5
Question. Two points A and B move from rest along a straight line with constant acceleration f and f ‘ respectively. If A takes m sec. more than B and describes ‘n’units more than B in acquiring the same speed then
(a) ( f – f ‘)m2 = ff ‘n
(b) ( f + f ‘)m2 = ff ‘n
(c) 1/2 ( f – f ‘)m = ff ‘n2
(d) ( f + f ‘)n = 1/2 ff ‘m2
Question. A li ard, at an initial distance of 21 cm behind an insect, moves from rest with an acceleration of 2 cm/s2 and pursues the insect which is crawling uniformly along a straight line at a speed of 20 cm/s. Then the lizard will catch the insect after
(a) 20 s
(b) 1 s
(c) 21 s
(d) 24 s
Question. If θ denotes the acute angle between the curves, y = 10 – x2 and y = 2 + x2 at a point of their intersection, then |tan θ| is equal to:
(a) 4/9
(b) 8/15
(c) 7/17
(d) 8/17
Question. If the curves y2 = 6x,9x2 + by2 =16 intersect each other at right angles, then the value of b is :
(a) 7/2
(b) 4
(c) 9/2
(d) 6
Question. The function, f(x) = (3x – 7)x2/3 , x ∈ R, is increasing for all x lying in :
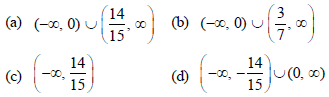
Ans : A
Question. Let f(x) = ex – x and g(x) = x2 – x, x ∈ R. Then the set of all x ∈ R, where the function h(x) = (fog) (x) is increasing, is :
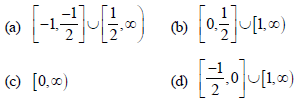
Ans : B
Question. If the function f : R – {1, –1} → A defined by f(x) = x2/(1−x2), is surjective, then A is equal to:
(a) R – {–1}
(b) [0, “)
(c) R – [–1, 0)
(d) R – (–1, 0)
Question. The position of a moving car at time t is given by f (t) = at2 + bt + c, t > 0, where a, b and c are real numbers greater than 1. Then the average speed of the car over the time interval [t1, t2] is attained at the point :
(a) (t2 – t1)/2
(b) a(t2 – t1) + b
(c) (t1 + t2)/2
(d) 2a(t1 + t2) + b
Question. If the surface area of a cube is increasing at a rate of 3.6 cm2/sec, retaining its shape; then the rate of change of its volume (in cm3/sec.), when the length of a side of the cube is 10 cm, is :
(a) 18
(b) 10
(c) 20
(d) 9
Question. Let f: [0 : 2] → R be a twice differentiable function such that f”(x) > 0, for all x∈(0, 2). If Φ(x) = f(x) + f(2 – x), then Φ is :
(a) increasing on (0, 1) and decreasing on (1, 2).
(b) decreasing on (0, 2)
(c) decreasing on (0, 1) and increasing on (1, 2).
(d) increasing on (0, 2)
Question. The function f defined by f(x) = x3 – 3x2 + 5x + 7, is :
(a) increasing in R.
(b) decreasing in R.
(c) decreasing in (0, ∞) and increasing in (– ∞ , 0).
(d) increasing in (0, ∞) and decreasing in (– ∞, 0).
Question. Let f(x) = sin4x + cos4x. Then f is an increasing function in the interval :
(a) ]5π/8, 3π/4]
(b) ]π/2, 5π/8]
(c) ]π/4, π/2]
(d) ]0, π/4]
Question. The maximum value of the function f(x) = 3x3 – 18x2 + 27 x – 40 on the set S = {x ∈ R : x2 + 30 ≤ 11x} is :
(a) – 122
(b) – 222
(c) 122
(d) 222
Question. Let x, y be positive real numbers and m, n positive integers. The maximum value of the expression (xmyn) / ( (1+x2m)(1+y2n) ) is :
(a) 1
(b) 1/2
(c) 1/4
(d) (m + n)/6mn
Question. Let f and g be two differentiable functions on R such that f'(x) > 0 and g'(x) < 0 for all x ∈ R . Then for all x:
(a) f(g (x)) > f (g (x – 1))
(b) f(g (x)) > f (g (x + 1))
(c) g(f (x)) > g (f (x – 1))
(d) g(f (x)) < g (f (x + 1))
Question.Statement-1: The equation x log x = 2 – x is satisfied by at least one value of x lying between 1 and 2.
Statement-2: The function f (x) = x log x is an increasing function in [l, 2] and g (x) = 2 – x is a decreasing function in [1, 2] and the graphs represented by these functions intersect at a point in [1, 2]
(a) Statement-1 is true; Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(b) Statement-1 is true; Statement-2 is true; Statement-2 is not correct explanation for Statement-1.
(c) Statement-1 is false, Statement-2 is true.
(d) Statement-1 is true, Statement-2 is false.
Question. Two ships A and B are sailing straight away from a fixed point O along routes such that ∠AOB is always 120° . At a certain instance, OA = 8 km, OB = 6 km and the ship A is sailing at the rate of 20 km/hr while the ship B sailing at the rate of 30 km/hr. Then the distance between A and B is changing at the rate (in km/hr):
(a) 260/√37
(b) 260/37
(c) 80/√37
(d) 80/37
Question. A spherical balloon is being inflated at the rate of 35cc/ min. The rate of increase in the surface area (in cm2/min.) of the balloon when its diameter is 14 cm, is :
(a) 10
(b) √10
(c) 100
(d) 10√10
Question. How many real solutions does the equation x7 + 14x5 + 16x3 + 30x – 560 = 0 have?
(a) 7
(b) 1
(c) 3
(d) 5
Question. If the tangent to the curve, y = f (x) = xlogex, (x > 0) at a point (c, f(c)) is parallel to the line segement oining the points (1, 0) and (e, e), then c is equal to:
(a) (e – 1)/e
(b) e(1/(e-1))
(c) e(1/(1-e))
(d) e/(e -1)
Question. The function f(x) = x/2 + x/2 has a local minimum at
(a) x = 2
(b) x = -2
(c) x = 0
(d) x = 1
Question. The real number x when added to its inverse gives the minimum value of the sum at x equal to
(a) –2
(b) 2
(c) 1
(d) –1
Question. Which of the following points lies on the tangent to the curve x4ey + 2√(y+1) =3 at the point (1, 0)?
(a) (2, 2)
(b) (2, 6)
(c) (– 2, 6)
(d) (– 2, 4)
Question. If
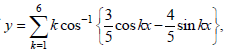
then dy/dx at x = 0 is ___________.
Ans : 91
Very Short Answer Type Questions
Question. The total cost C(x) associated with provision of free mid-day meals to x students of a school in primary classes is given by C(x) = 0.005x3 – 0.02x2 + 30x + 50 If the marginal cost is given by rate of change dC/dx of total cost, write the marginal cost of food for 300 students. What value is shown here?
Answer. Given, C(x) = 0.005x3 – 0.02x2 + 30x + 50

= 1350 – 12 + 30 = 1368.
The value indicated here is that a kind of care and concern is shown towards the health of students of primary classes by providing free mid-day meal to them.
Question. The total expenditure (in ₹) required for providing the cheap edition of a book for poor and deserving students is given by R(x) = 3x2 + 36x where x is the number of sets of books. If the marginal expenditure is defined as dR/dx, write the marginal expenditure required for 1200 such sets. What value is reflected in this question?
Answer. Here, R(x) = 3x2 + 36x,

The value indicated here is that a kind of help is provided to poor and deserving students who want to study but they don’t have sources to purchase books.
Question. For the curve y = 3x2 + 4x, Find the slope of the tangent to the curve at the point whose x-coordinate is –2.
Answer. The given curve is y = 3x2 + 4x.
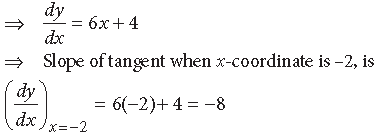
Short Answer Type Questions
Question. Find the intervals in which the following function is (a) increasing (b) decreasing :
f(x) = 2x3 – 9x2 + 12x + 20
Answer. Given : f(x) = 2x3 + 9x2 + 12x + 20
⇒ f’ (x) = 6x2 + 18x + 12
= 6(x2 + 3x + 2) = 6(x + 1)(x + 2)

Question. Find the point on the curve 9y2 = x3, where the normal to the curve makes equal intercepts on the axes.
Answer. We have, 9y2 = x3 … (i)
Differentiating (i) w.r.t. x, we get


Question. Find the equation of the tangent and normal to the curve x = a sin3θ and y = a cos3θ at θ = π/4
Answer. We have, x = a sin3θ; y = a cos3θ

Question. Find the equations of the tangent and normal to the curve
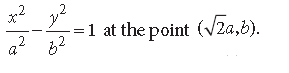
Answer.

Question. Show that the equation of normal at any point t on the curve x = 3 cost – cos3t and y = 3 sint – sin3t is 4(y cos3t – x sin3t)= 3 sin 4t.
Answer. x = 3 cost – cos3t and y = 3 sint – sin3 t
Now,
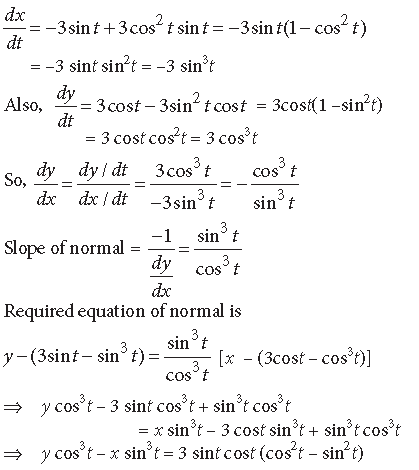
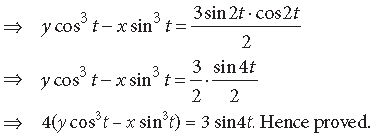
Question. The equation of tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x –5. Find the values of a and b
Answer. We have, y2 = ax3 + b
Differentiating w.r.t. x, we get

So, equation of tangent at the point (2, 3) is
y – 3 = 2a (x – 2)
⇒ y = 2ax – 4a + 3 …(i)
But we are given that equation of tangent at (2, 3) is
y = 4x – 5 …(ii)
∴ On comparing (i) and (ii), we get
2a = 4 ⇒ a = 2
∵ Point (2, 3) lies on the curve y2 = ax3 + b,
∴ (3)2 = (2)3 a + b ⇒ 9 = 8a + b
⇒ 9 = 8 × 2 + b ⇒ b = –7
Question. Find the angle of intersection of the curves y2 = 4ax and x2 = 4by
Answer. The given curves are
y2 = 4ax … (i)
x2 = 4by …(ii)
Solving (i) and (ii), we get



Question. Show that the equation of tangent to the parabola y2 = 4ax at (x1, y1) is yy1 = 2a(x + x1)
Answer. The Given parabola is
y2 = 4ax … (i)
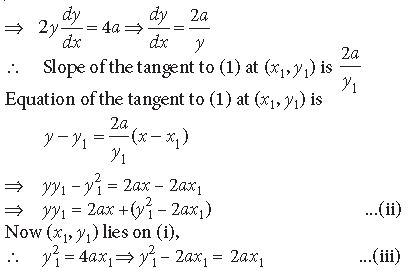
From (ii) and (iii), we get
yy1 = 2ax + 2ax1 = 2a(x + x1)
This is the equation of the tangent to (i) at (x1, y1).
Question. Find the points on the curve x2 + y2 – 2x – 3 = 0 at which the tangents are parallel to x-axis.
Answer. The given curve is
x2 + y2 – 2x – 3 = 0. …(i)
Differentiating with respect to x, we get
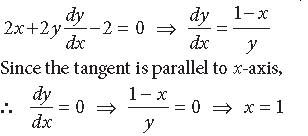
Putting the value of x = 1 in (i), we get
(1)2 + y2 – 2(1) – 3 = 0 ⇒ y2 = 4
⇒ y = ±2
∴ The points are (1, 2) and (1, –2).
Question. Find the point on the curve y = x3 – 11x + 5 at which the equation of tangent is y = x – 11.
Answer. y = x3 – 11x + 5 …(i)
Differentiating (i) w.r.t. x, we get
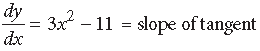
Also, equation of tangent is y = x – 11
∴ its slope = 1.
So 3x2 – 11 = 1 ⇒ x2 = 4
∴ x = ± 2
Putting the values of x in (i), we get
y = 23 – 11(2) + 5 = 8 – 22 + 5 = – 9
y = (– 2)3 – 11(–2) + 5 = – 8 + 22 + 5 = 19
So points are (2, –9) and (–2, 19).
But only (2, –9) satisfies the equation of tangent.
So required point is (2, –9).
Question. Find the intervals in which the function f(x) = (x – 1)3(x – 2)2 is.
(a) increasing
(b) decreasing.
Answer. Here, f(x) = (x – 1)3 · (x – 2)2
⇒ f’ (x) = 3(x – 1)2(x – 2)2 + (x – 1)3 · 2(x – 2)
= (x – 1)2(x – 2)[3(x – 2) + 2(x – 1)]
= (x – 1)2 (x – 2) (5x – 8)
(a) For f to be an increasing function,
f’ (x) > 0
⇒ (x – 1)2 (x – 2)(5x – 8) > 0
⇒ (x – 2)(5x – 8) > 0 [… (x – 1)2 > 0 ∀ x ∈ R]
⇒ x – 2 > 0, 5x – 8 > 0 or x – 2 < 0, 5x – 8 < 0
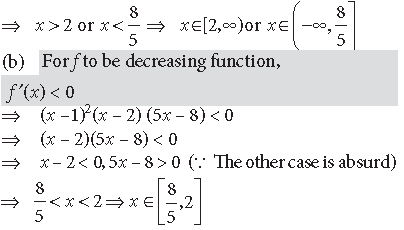
Question. Find the intervals in which the following function is (a) increasing (b) decreasing :
f (x) = 2x3 – 15x2 + 36x + 17
Answer. We have, f (x) = 2x3 – 15x2 + 36x + 17
⇒ f’ (x) = 6x2 – 30x + 36 = 6(x2 – 5x + 6)
⇒ f’ (x) = 6(x – 3)(x – 2)
Now, for critical points f’ (x) = 0
⇒ 6(x – 3)(x – 2) = 0 ⇒ x = 2, 3
The points x = 2, x = 3 divide real line into disjoint
intervals (– ∞, 2), (2, 3) and (3, ∞).
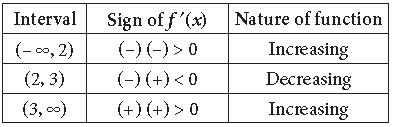
Hence, f (x) is increasing in (– ∞, 2] U [3, ∞) and decreasing in [2, 3].
Question. Find the intervals in which the function f given by
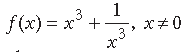
(i) increasing
(ii) decreasing
Answer.
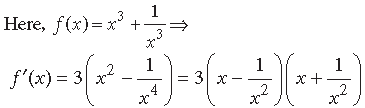
So, critical points are x = –1, x = 1.
Also f (x) is not defined for x = 0.
So, disjoint intervals are (–∞, –1), (–1, 0), (0, 1), (1, ∞).
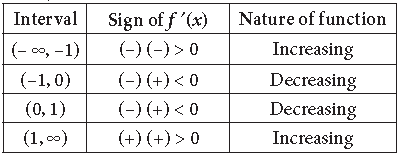
Hence, f(x) is increasing in (–∞, – 1] U [1, ∞) and decreasing in [–1, 0) U (0, 1]
Question. Find the intervals in which the function given by f(x) = sin x + cosx, 0 ≤ x ≤ 2π is
(a) increasing,
(b) decreasing.
Answer. The given function is
f(x) = sin x + cosx; 0 < x < 2π
⇒ f’ (x) = cos x – sin x
Now f’ (x) = 0 ⇒ cos x – sin x = 0

Question. Find the intervals in which the following function is (a) increasing (b) decreasing :
f(x) = x4 – 8x3 + 22x2 – 24x + 21
Answer. The given function is
f(x) = x4 – 8x3 + 22x2 – 24x + 21
⇒ f ‘(x) = 4x3 – 24x2 + 44x – 24
= 4(x3 – 6x2 + 11x – 6)
= 4(x – 1)(x2 – 5x + 6)
= 4(x – 1)(x – 2)(x – 3)
Thus f ‘(x) = 0 ⇒ x = 1, 2, 3.
Hence, possible disjoint intervals are
(–∞, 1), (1, 2), (2, 3) and (3, ∞).
In the interval (–∞, 1), f ‘ (x) < 0
In the interval (1, 2), f'(x) >0
In the interval (2, 3), f'(x) < 0
In the interval (3, ∞), f'(x) >0
∴ f is increasing in [1, 2] U [3, ∞) and f is
decreasing in (–∞, 1] U [2, 3].
Question.
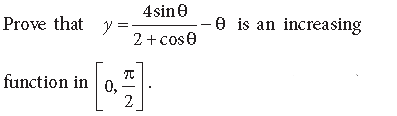
Answer.
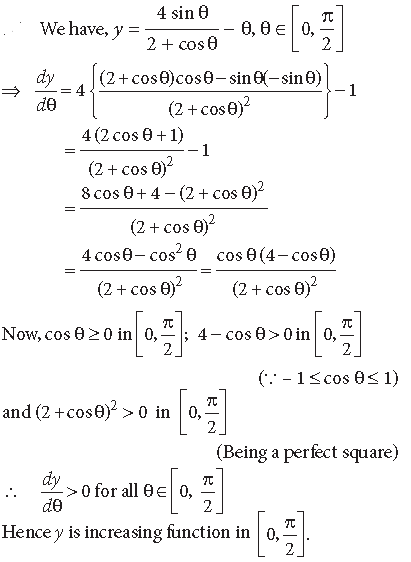
Long Answer Type Questions
Question. Find the equations of the tangent and normal to the parabola y2 = 4ax at the point (at2, 2at).
Answer. the given parabola is
y2 = 4ax …(i)
and the point is P(at2, 2at).
Differentiating (i) w.r.t. x, we get

Question. Find the equations of the normals to the curve y = x3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Answer. The given curve is
y = x3 + 2x + 6 …(i)

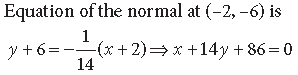
Question. Find the equations of the tangent and the normal to the curve x = 1 – cos θ; y = θ – sin θ at θ = π/4
Answer. Given curves are x = 1 – cos θ and y = θ –sin θ
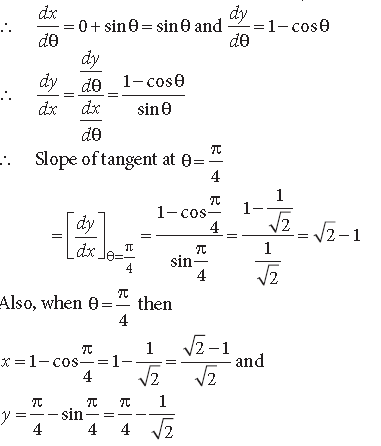
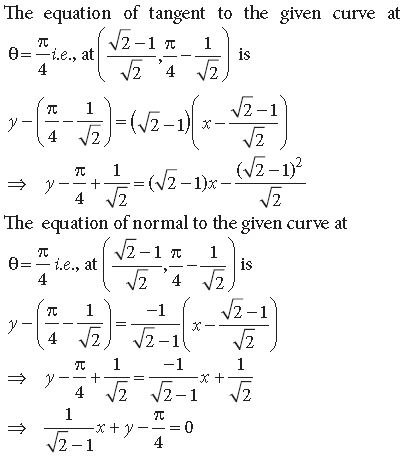
Question. Find the local maxima and local minima of the function f(x) = sin x – cos x, 0 < x < 2π. Also find the local maximum and local minimum values.
Answer. We have, f(x) = sinx – cosx
⇒ f’ (x) = cos x + sinx
For maxima or minima, f’ (x) = 0
⇒ cos x + sin x = 0 ⇒ tan x = –1
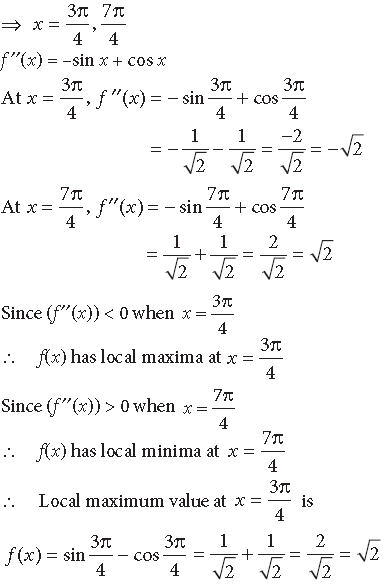
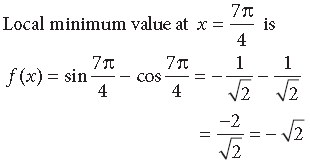
Question. Find the minimum value of (ax + by), where xy = c2.
Answer. Let u = ax+ by, where xy = c2

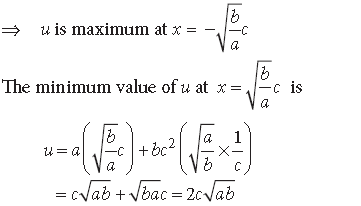
Question. Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x –3.
Answer. Let P (h, k) be the coordinates of the point on given parabola.
∴ k = h2 + 7h + 2 …(i)
The distance S of P from the straight line
– 3x + y + 3 = 0 is
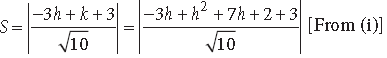
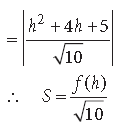
⇒ S will be maximum or minimum according as f(h) is maximum or minimum.
Since, f(h) = h2 + 4h + 5
f’ (h) = 2h + 4
For maxima or minima, f’ (h) = 0
⇒ 2h + 4 = 0 ⇒ h = – 2
Also, f” (h) = 2 > 0 when h = – 2
S is minimum at h = –2
Putting this value in (i), we get
k = (–2)2 + 7(–2) + 2 = 4 – 14 + 2 = –8
∴ The required coordinates are (–2, –8)
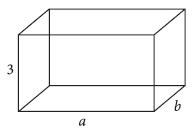
Question. A tank with rectangular base and rectangular sides open at the top is to be constructed so that its depth is 3 m and volume is 75 m3. If building of tank costs ₹ 100 per square metre for the base and ₹ 50 per square metre for the sides, find the cost of least expensive tank.
Answer. Let a m and b m be the sides of the base of the tank.

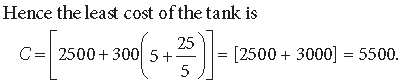
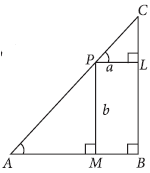
Question. A point on the hypotenuse of a right triangle is at distance ‘a’ and ‘b’ from the sides of the triangle. Show that the minimum length of the hypotenuse is
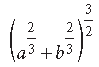
Answer. Let P be any point on the hypotenuse of the given right triangle.
Let PL = a, PM = b and AM = x.
Clearly, ΔCPL and ΔPAM are similar
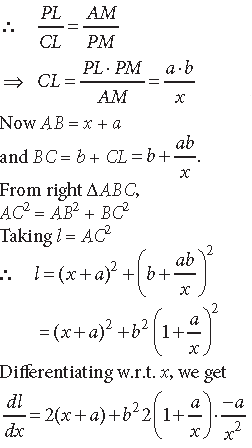

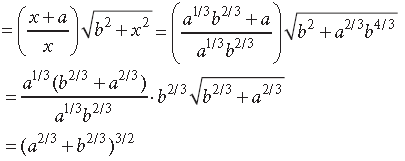
Question. Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
Answer. Let r and h be the radius and height of the cylindrical can respectively.
Therefore, the total surface area of the closed cylinder is given by
S = 2πrh + 2πr2 = 2πr(r + h) …(i)
Given volume of the can = 128π cm3
Also volume (V) = πr2h

Question. Show that the semi vertical angle of the cone of the maximum volume and of given slant height is cos−1 1/√3
Answer. Let θ be the semi-vertical angle of the cone, V its volume, h its height, r base radius and slant height l.
Then from ΔOAP,
r = l sin θ, h = l cos θ
Now
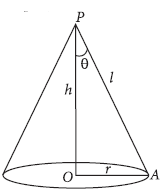
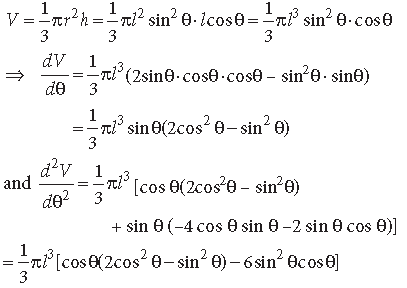
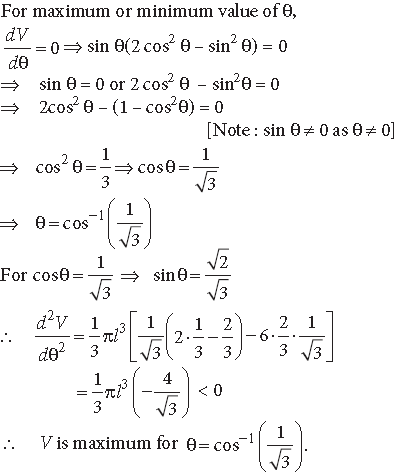
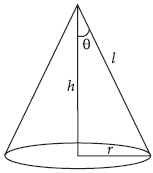
Question. Prove that the semi vertical angle of the right circular cone of given volume and least curved surface area is cot−1 √2.
Answer. Let r, h, l, V and S be respectively the base radius, height, slant height, volume and curved surface of the cone.
Then,
l2 = r2 + h2
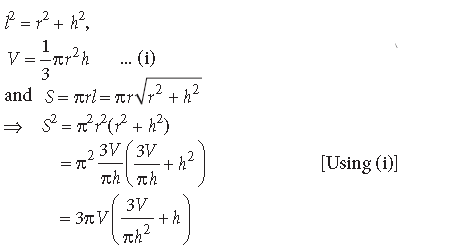
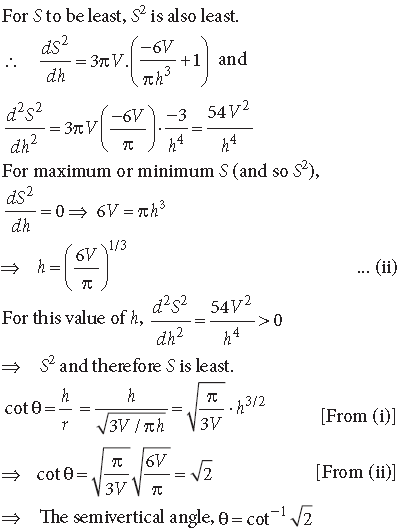
Question. Prove that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3. Also find the maximum volume.
Answer. Let r and h be the base radius and height of cylinder respectively.
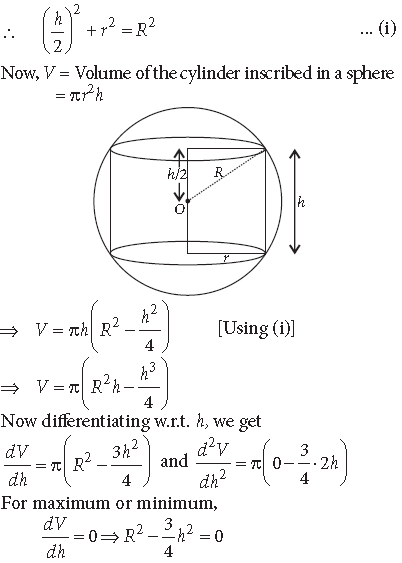
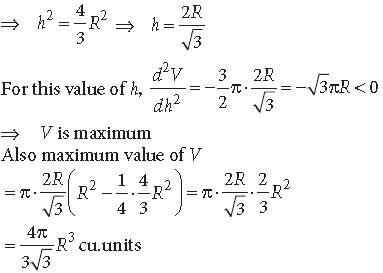
Question. The sum of the perimeters of a circle and a square is k, where k is some constant. Prove that the sum of their areas is least when the side of the square is equal to the diameter of the circle.
Answer. Let a be the side of the given square and r be the radius of the circle.
By hypothesis 4a + 2πr = k
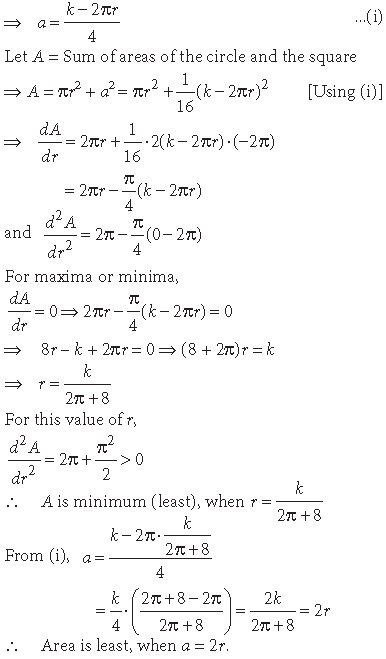
Question. Show that a cylinder of a given volume which is open at the top has minimum total surface area, when its height is equal to the radius of its base.
Answer. Let r and h be the base radius and height of the cylinder respectively and volume of cylinder, V = πr2h
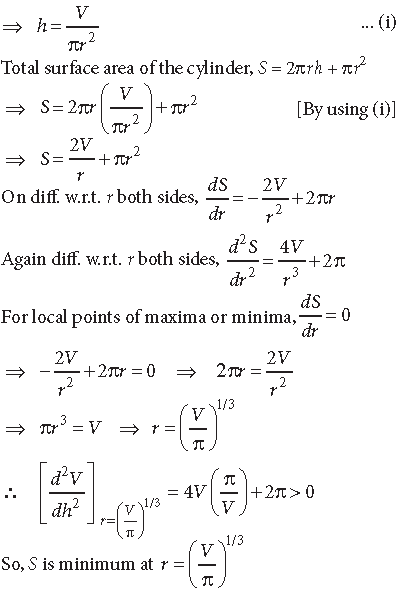
Now, πr3 = V ⇒ πr3 = πr2h ⇒ r = h
Hence, the cylinder of a given volume which is open at the top has minimum total surface area, when it height is equal to the radius of its base.
Question. A window is of the form of a semi-circle with a rectangle on its diameter. The total perimeter of the window is 10 m. Find the dimension of the window to admit maximum light through the whole opening.
Answer. Let ABCD be a rectangle and let the semi-circle is described on the side AB as its diameter.
Let AB = 2x and AD = 2y. Let P = 10 m be the given perimeter of window.
Therefore, 10 = 2x + 4y + πx ⇒ 4y = 10 – 2x – πx …(i)


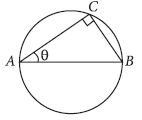
Question. AB is a diameter of a circle and C is any point on the circle. Show that the area of ΔABC is maximum , when it is isosceles.
Answer. Here BA is a diameter of the given circle, of radius = r.
Let ∠CAB = θ
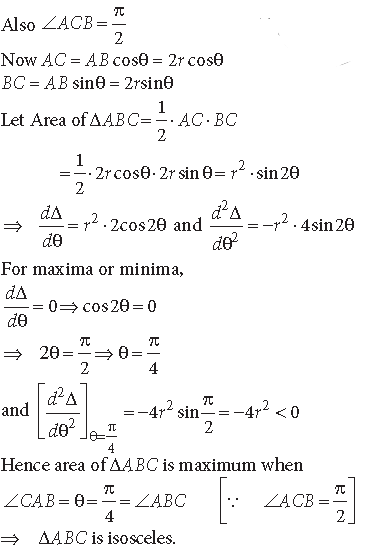
Question. Find the point P on the curve y2 = 4ax which is nearest to the point
Answer. The given parabola is
y2 = 4ax …(i)
Let Q(11a, 0).
Any point on (i) is P(at2, 2at)
∴ PQ2 = (at2 – 11a)2 + (2at – 0)2
Let l = PQ2 = a2t4 – 18 a2t2 + 121a2
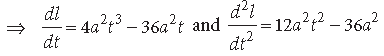
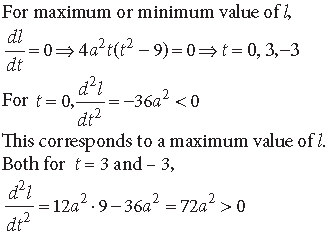
∴ This corresponds to a minimum value of l i.e., of PQ2 and therefore of PQ.
Thus, there are two such points P with coordinates,
(9a, 6a)and (9a – 6a) nearest to the given point Q.
Question. If the length of three sides of a trapezium other than base is 10 cm each, then find the area of the trapezium when it is maximum.
Answer. Let ABCD be the given trapezium
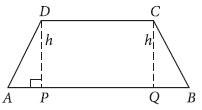
Then AD = DC = CB = 10 cm
In ΔAPD and ΔBQC
DP = CQ = h
AD = BC = 10 cm
∠DPA = ∠CQB = 90°
∴ ΔAPD ≅ ΔBQC (by R.H.S. congruency)
⇒ AP = QB = x cm (Say)
∴ AB = AP + PQ + QB
= x + 10 + x = (2x + 10)cm
Also from ΔAPD,
AP2 + PD2 = AD2 ⇒ x2 + h2 = 102
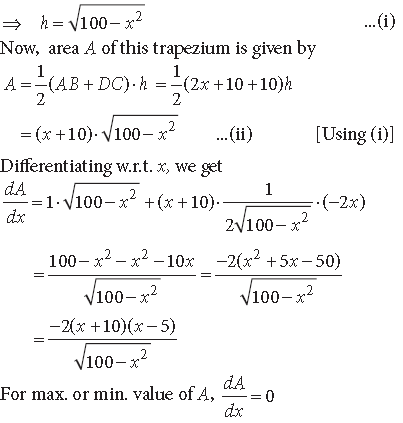
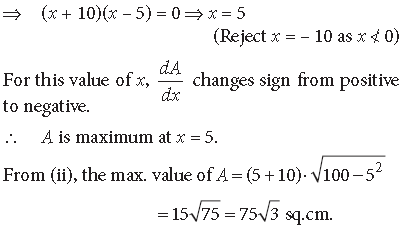
Question. Find the area of the greatest rectangle that can be inscribed in an ellipse
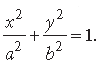
Answer. Let ABCD be a rectangle inscribed in the ellipse,
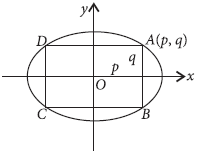
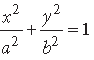
Let AB = 2q, DA = 2p.
Then coordinates of A are (p, q).
As A lies on the ellipse so
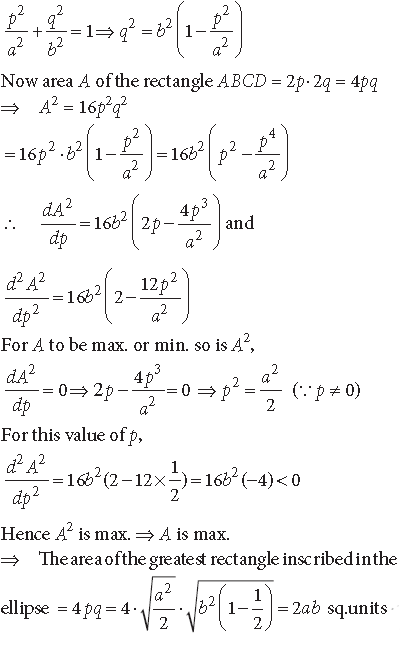
Question. Prove that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of a radius r is 4r/3
Answer.
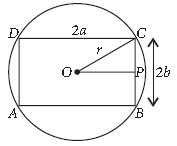
91. Prove that of all the rectangles inscribed in a given circle, the square has the maximum area.
Answer. Let the radius of given circle = r
Let 2a and 2b are the lengths of the sides of any inscribed rectangle in the given circle.
Then from ΔOPC,
OC2 = OP2 + PC2
⇒ r2 = a2 + b2
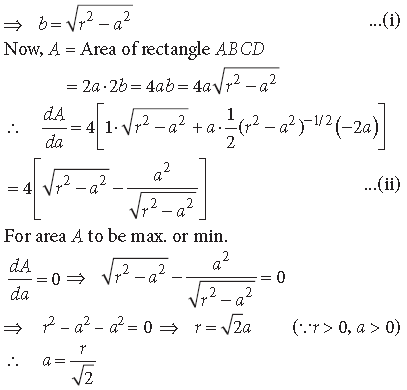
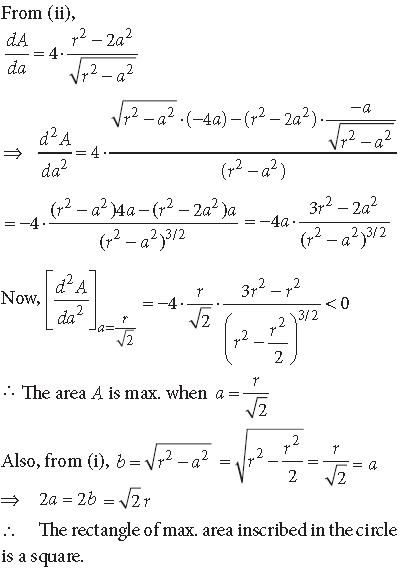
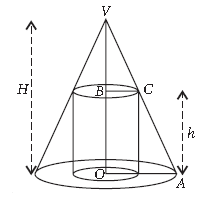
Question. Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone, is half that of the cone.
Answer. Let R and H be the base radius and height of the given cone and r, h be the same for the inscribed cylinder. Clearly, ΔVBC is similar to ΔVOA

Question. Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 times the radius of the base.
Answer. Let r be the base radius of the cone, l be the slant height and h be its height. Let V be its volume and S be its curved surface.

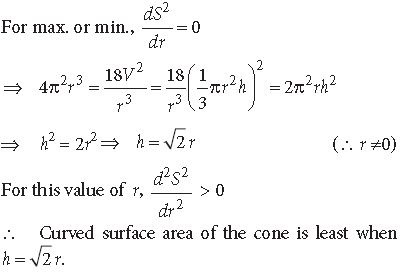
Question. Show that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
Answer. Let r be the radius of the circular base, h be the height and S be the total surface area of a right circular cylinder, then
S = 2πr2 + 2πrh is given to be a constant.
Let V be the volume of the cylinder, then

So, volume is maximum when the height is equal to the diameter.
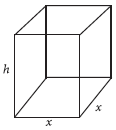
Question. An open box with a square base is to be made out of a given quantity of cardboard of area c2 square units. Show that the maximum volume of the box is c36√3 cubic units.
Answer. Let h be height and x be the side of the square base of the open box. Then its area = x × x + 4 h × x = c2
(given)
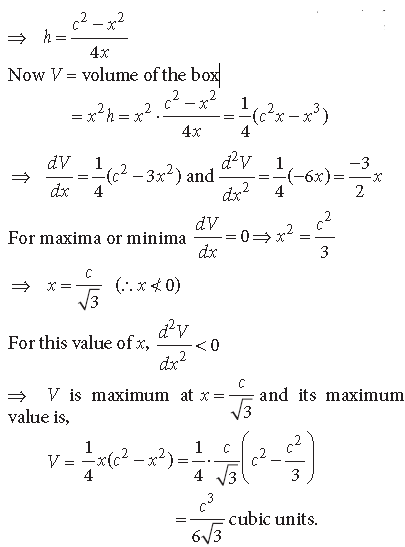
Question. Prove that the area of a right angled triangle of given hypotenuse is maximum when the triangle is isosceles.
Answer. Let ΔABC be gives right angled triangle with sides a, b and hypotenuse c.
We have, a2 + b2 = c2

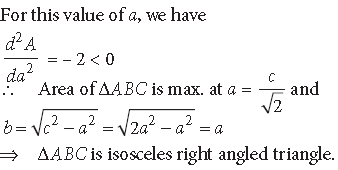
Question. Show that of all the rectangles with a given perimeter, the square has the largest area.
Answer. Let x and y be the length and breadth of the rectangle whose perimeter (P) is given.

Question. Show that of all the rectangles of given area, the square has the smallest perimeter.
Answer. Let x and y be the lengths and breadth of rectangle of given area A, then we have,
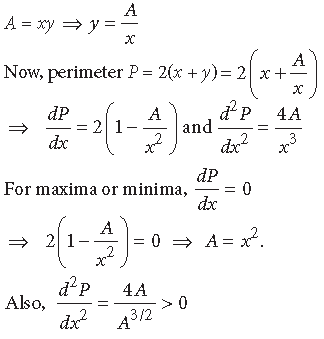
∴ Perimeter of rectangle is minimum, when x = √A
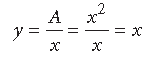
So, perimeter of rectangle is minimum, when y = x
i.e. rectangle is square.
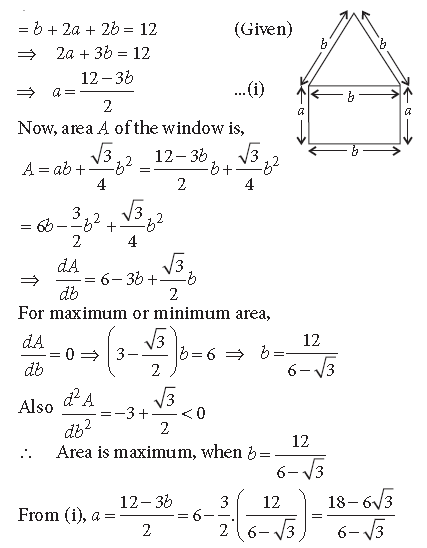
Question. A window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the rectangle that will produce the largest area of the window.
Answer. Let a be the breadth and b be the length of rectangle and b be the side of equilateral triangle. Total perimeter of the window
Question. Find the point on the curve y2 = 2x which is at a minimum distance from the point (1, 4).
Answer. Let the point on y2 = 2x, which is at a min.
distance from Q(1, 4), be P(x, y).
∴ We have to minimise
s = PQ2 = (x – 1)2 + (y – 4)2
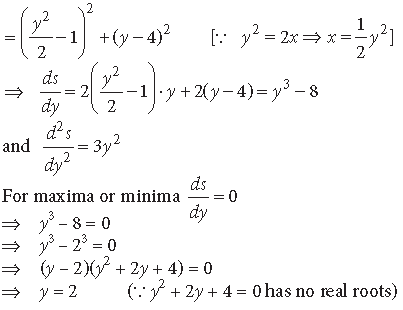
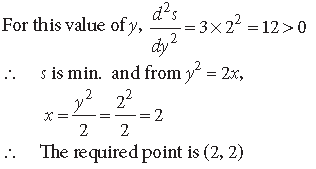
Question. Show that a right circular cylinder which is open at the top and has a given surface area, will have the greatest volume, if its height is equal to the radius of its base.
Answer. Let S, V, r and h be the surface area, volume, radius and height of the cylinder. Then

Question. A manufacturer can sell x items at a price of

Answer. Let S(x) be the selling price of x items and let C(x) be the cost price of x items. Then, we have

Thus x = 240 is a point of maxima. Hence, the manufacturer can earn maximum profit, if he sells 240 items.
Question. Show that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is (1/3)h.
Answer. Let a cylinder be inscribed in a cone of radius
R and height h.
Let the cylinder’s radius be r and its height be h1
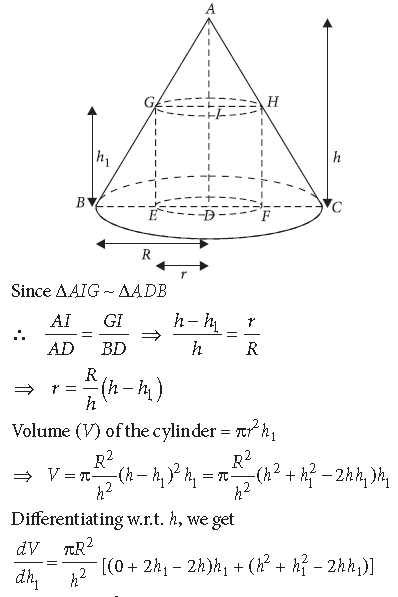


Question. Show that the volume of the greatest cylinder which can be inscribed in a cone of height h and semi-vertical angle α is 4/27 πh3 tan2 α .
Answer. Let R be the radius, H be the height of the cylinder inscribed in cone, r be the radius and h be the height of the cone.
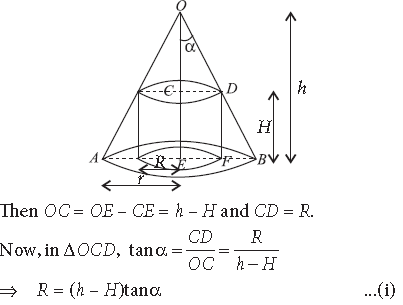
where α is the semi-vertical angle of the cone
As α is given. ∴ It is constant.
Let V be the volume of the cylinder.
∴ V= πR2H = π[(h – H)2 tan2α]H (Using (i))
V = πH · (h – H)2 tan2α …(ii)
Differentiating (ii) w.r.t. H, we get
dV/dH = π[(h − H)2 X 1+ H · 2(h − H)(−1)]tan2 α
= π tan2 α(h2 − 4hH + 3H2 ) …(iii)
= πtan2 α(h – H)(h – 3H)


Question. Find the point on the curve x2 = 8y which is nearest to the point (2, 4).
Answer. Let P(x, y) be a point on x2 = 8y and Q ≡(2, 4).