VBQs Straight Lines Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Straight Lines Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Straight Lines VBQs Class 11 Mathematics
Question. Let A (h, k), B(1, 1) and C (2, 1) be the vertices of a right angled triangle with AC as its hypotenuse. If the area of the triangle is 1square unit, then the set of values which ‘k’ can take is given by
(a) {–1, 3}
(b) {–3, –2}
(c) {1, 3}
(d) {0, 2}
Answer
A
Question. If a vertex of a triangle is (1, 1) and the mid points of two sides through this vertex are (–1, 2) and (3, 2) then the centroid of the triangle is
(a) (-1, 7/3)
(b) (-1/3, 7/3)
(c) (1, 7/3)
(d) (1/3, 7/3)
Answer
C
Question. A triangle has a vertex at (1, 2) and the mid points of the two sides through it are (–1, 1) and (2, 3). Then the centroid of this triangle is :
(a) (1, 7/3)
(b) (1/3, 2)
(c) (1/3, 1)
(d) (1/3, 5/3)
Answer
B
Question. Let the orthocentre and centroid of a triangle be A(–3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter, is :
(a) 2√10
(b) 3√(5/2)
(c)3√5/2
(d) √10
Answer
B
Question. A point on the straight line, 3x + 5y = 15 which is equidistant from the coordinate axes will lie only in :
(a) 4th quadrant
(b) 1st quadrant
(c) 1st and 2nd quadrants
(d) 1st, 2nd and 4th quadrants
Answer
C
Question. Two vertical poles of heights, 20 m and 80 m stand apart on a hori ontal plane. The height (in meters) of the point of intersection of the lines oining the top of each pole to the foot of the other, from this hori ontal plane is :
(a) 15
(b) 18
(c) 12
(d) 16
Answer
D
Question. A square, of each side 2, lies above the x-axis and has one vertex at the origin. If one of the sides passing through the origin makes an angle 30° with the positive direction of the x-axis, then the sum of the x-coordinates of the vertices of the square is :
(a) 2√3 -1
(b) 2√3 – 2
(c) √3 – 2
(d) √3 -1
Answer
B
Question. The points (0, 8/3), (1, 3) and (82, 30):
(a) form an acute angled triangle.
(b) form a right angled triangle.
(c) lie on a straight line.
(d) form an obtuse angled triangle.
Answer
C
Question. A light ray emerging from the point source placed at P( 1, 3) is reflected at a point Q in the axis of x. If the reflected ray passes through the point R (6, 7), then the abscissa of Q is:
(a) 1
(b) 3
(c) 7/2
(d) 5/2
Answer
D
Question. If a line intercepted between the coordinate axes is trisected at a point A(4, 3), which is nearer to x-axis, then its equation is:
(a) 4x – 3y = 7
(b) 3x + 2y = 18
(c) 3x + 8y = 36
(d) x + 3y = 13
Answer
B
Question. Given three points P, Q, R with P(5, 3) and R lies on the x-axis. If equation of RQ is x – 2y = 2 and PQ is parallel to the x-axis, then the centroid of ΔPQR lies on the line:
(a) 2x + y – 9 = 0
(b) x – 2y + 1 = 0
(c) 5x – 2y = 0
(d) 2x – 5y = 0
Answer
D
Question. If the equation of the locus of a point equidistant from the point (a1, b1) and (a2, b2 ) is (a1 – b2 )x + (a1 – b2 ) y + c = 0 , then the value of c is
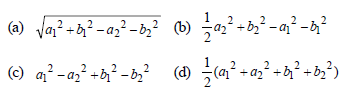
Answer
B
Question. A triangle ABC lying in the first quadrant has two vertices as A(1, 2) and B(3, 1). If ∠BAC = 90°, and ar (ΔABC) = 5√5 sq. units, then the abscissa of the vertex C is:
(a) 1 + √5
(b) 1 + 2√5
(c) 2 + √5
(d) 2√5 – 1
Answer
B
Question. If the perpendicular bisector of the line segment oining the points P (1, 4) and Q (k, 3) has y-intercept equal to – 4, then a value of k is :
(a) – 2
(b) – 4
(c) √14
(d) √15
Answer
B
Question. Locus of centroid of the triangle whose vertices are (a cos t, asin t), (bsin t,- bcos t) and (1, 0), where t is a parameter, is
(a) (3x+1)2 + (3y)2 = a2 − b2
(b) (3x−1)2 + (3y)2 = a2 − b2
(c) (3x−1)2 + (3y)2 = a2 + b2
(d) (3x+1)2 + (3y)2 = a2 + b2
Answer
C
Question. A triangle with vertices (4, 0), (–1, –1), (3, 5) is
(a) isosceles and right angled
(b) isosceles but not right angled
(c) right angled but not isosceles
(d) neither right angled nor isosceles
Answer
A
Question. If a straight line passing through the point P(–3, 4) is such that its intercepted portion between the coordinate axes is bisected at P, then its equation is :
(a) 3x – 4y + 25 = 0
(b) 4x – 3y + 24 = 0
(c) x – y + 7 = 0
(d) 4x + 3y = 0
Answer
B
Question. If in a parallelogram ABDC, the coordinates of A, B and C are respectively (1, 2), (3, 4) and (2, 5), then the equation of the diagonal AD is :
(a) 5x – 3y + 1 = 0
(b) 5x + 3y – 11 = 0
(c) 3x – 5y + 7 = 0
(d) 3x + 5y – 13 = 0
Answer
A
Question. Let ƒ: R → R be defined as
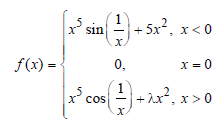
The value of λ for which ƒ” (0) exists, is ______.
Answer
5
Question. The point (2, 1) is translated parallel to the line L : x – y = 4 by 2√3 units. If the new points Q lies in the third quadrant, then the equation of the line passing through Q and perpendicular to L is :
(a) x + y = 2 – √6
(b) 2x + 2y =1- √6
(c) x + y = 3- 3√6
(d) x + y = 3- 2√6
Answer
D
Question. A straight line L through the point (3, – 2) is inclined at an angle of 60 to the line 3 x + y = 1. If L also intersects the x-axis, then the equation of L is :
(a) y + √3 x + 2 – 3√3 = 0
(b) √3 y + x – 3 + 2√3 = 0
(c) y – √3 x + 2 + 3√3 = 0
(d) √3 y – x + 3 + 2√3 = 0
Answer
C
Question. The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1) (1, 1) and (1, 0) is :
(a) 2 + √2
(b) 2 – √2
(c) 1 + √2
(d) 1 – √2
Answer
B
Question. Let C be the centroid of the triangle with vertices (3, –1), (1, 3) and (2, 4). Let P be the point of intersection of the lines x + 3y – 1 = 0 and 3x – y + 1 = 0. Then the line passing through the points C and P also passes through the point:
(a) (–9, –6)
(b) (9, 7)
(c) (7, 6)
(d) (–9, –7)
Answer
A
Question. Slope of a line passing through P(2, 3) and intersecting the line x + y = 7 at a distance of 4 units from P, is:
(a) (1 – √5)/(1 + √5)
(b) (1 – √7)/(1 + √7)
(c) (√7 – 1)/(√7 + 1)
(d) (√5 – 1)/(√5 + 1)
Answer
B
Question. A point P moves on the line 2x – 3y + 4 = 0. If Q(1, 4) and R(3, –2) are fixed points, then the locus of the centroid of ΔPQR is a line:
(a) with slope 3/2
(b) parallel to x-axis
(c) with slope 2/3
(d) parallel to y-axis
Answer
C
Question. If a ΔABC has vertices A(–1, 7), B(–7, 1) and C(5, –5), then its orthocentre has coordinates :
(a) ( – 3/5, 3/5)
(b) (–3, 3)
(c) (3/5, – 3/5)
(d) (3, –3)
Answer
B
Question. Let A(l, 0), B(6, 2) and C (3/2, 6) be the vertices of a triangle ABC. If P is a point inside the triangle ABC such that the triangles APC, APB and BPC have equal areas, then the length of the line segment PQ, where Q is the point (– 7/6, – 1/3), is _______ .
Answer
5
Question. If the line 3x + 4y – 24 = 0 intersects the x-axis at the point A and the y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is:
(a) (3, 4)
(b) (2, 2)
(c) (4, 3)
(d) (4, 4)
Answer
B
Question. A ray of light along x + √3y = √3 gets reflected upon reaching x-axis, the equation of the reflected ray is
(a) y = x + √3
(b) √3y = x – √3
(c) y = √3x – √3
(d) √3y = x -1
Answer
B
Question. Let A (–3, 2) and B (–2, 1) be the vertices of a triangle ABC. If the centroid of this triangle lies on the line 3x + 4y + 2 = 0, then the vertex C lies on the line :
(a) 4x + 3y + 5 = 0
(b) 3x + 4y + 3 = 0
(c) 4x + 3y + 3 = 0
(d) 3x + 4y + 5 = 0
Answer
B
Question. A straight line through a fixed point (2, 3) intersects the coordinate axes at distinct points P and Q. If O is the origin and the rectangle OPRQ is completed, then the locus of R is :
(a) 2x + 3y = xy
(b) 3x + 2y = xy
(c) 3x + 2y = 6xy
(d) 3x + 2y = 6
Answer
B
Question. A straight line through origin O meets the lines 3y = 10 – 4x and 8x + 6y + 5 = 0 at points A and B respectively. Then O divides the segment AB in the ratio :
(a) 2 : 3
(b) 1 : 2
(c) 4 : 1
(d) 3 : 4
Answer
C
Question. A ray of light is incident along a line which meets another line, 7x – y + 1 = 0, at the point (0, 1). The ray is then reflected from this point along the line, y + 2x = 1. Then the equation of the line of incidence of the ray of light is :
(a) 41x – 25y + 25 = 0
(b) 41x + 25y – 25 = 0
(c) 41x – 38y + 38 = 0
(d) 41x + 38y – 38 = 0
Answer
C
Question. Let L be the line passing through the point P(1, 2) such that its intercepted segment between the co-ordinate axes is bisected at P. If L1 is the line perpendicular to L and passing through the point (–2, 1), then the point of intersection of L and L1 is :
(a) (4/5, 12/5)
(b) (3/5, 23/10)
(c) (11/10, 29/10)
(d) (3/10, 17/5)
Answer
A
Question. If a variable line drawn through the intersection of the lines x/3 + y/4 = 1 and x/4 + y/3 = 1, meets the coordinate axes at A and B, (A ≠ B) , then the locus of the midpoint of AB is :
(a) 7xy = 6 (x + y)
(b) 4 (x + y)2 – 28 (x + y) + 49 = 0
(c) 6xy = 7 (x + y)
(d) 14 (x + y)2 – 97 (x + y) + 168 = 0
Answer
A
Question. The circumcentre of a triangle lies at the origin and its centroid is the mid point of the line segment oining the points (a2 + 1, a2 + 1) and (2a, – 2a), a ≠ 0. Then for any a, the orthocentre of this triangle lies on the line:
(a) y – 2ax = 0
(b) y – (a2 + 1)x = 0
(c) y + x = 0
(d) (a – 1)2x – (a + 1)2y = 0
Answer
D
Question. Let O(0, 0) and A(0, 1) be two fixed points. Then the locus of a point P such that the perimeter of ΔAOP is 4, is :
(a) 8x2 – 9y2 + 9y = 18
(b) 9x2 – 8y2 + 8y = 16
(c) 9x2 + 8y2 – 8y = 16
(d) 8x2 + 9y2 – 9y = 18
Answer
C
Question. Two vertices of a triangle are (0, 2) and (4, 3). If its orthocentre is at the origin, then its third vertex lies in which quadrant?
(a) third
(b) second
(c) first
(d) fourth
Answer
B
Question. In a triangle ABC, coordianates of A are (1, 2) and the equations of the medians through B and C are x + y = 5 and x = 4 respectively. Then area of ΔABC (in sq. units) is
(a) 5
(b) 9
(c) 12
(d) 4
Answer
B
Question. Two sides of a rhombus are along the lines, x – y + 1 = 0 and 7x – y – 5 = 0. If its diagonals intersect at (–1, –2), then which one of the following is a vertex of this rhombus?
(a) (1/3, – 8/3)
(b) – 10/3, – 7/3)
(c) (-3, -9)
(d) (-3, -8)
Answer
A
Question. If the line 2x + y = k passes through the point which divides the line segment oining the points (1,1) and (2,4) in the ratio 3 :2, then k equals :
(a) 29/5
(b) 5
(c) 6
(d) 11/5
Answer
C
Question. Let PS be the median of the triangle vertices P(2, 2), Q(6, –1) and R(7, 3). The equation of the line passing through (1, –1) and parallel to PS is:
(a) 4x + 7y + 3 = 0
(b) 2x – 9y – 11 = 0
(c) 4x – 7y – 11 = 0
(d) 2x + 9y + 7 = 0
Answer
D
Question. If a line L is perpendicular to the line 5x – y = 1, and the area of the triangle formed by the line L and the coordinate axes is 5, then the distance of line L from the line x + 5y = 0 is:
(a) 7/√5
(b) 5/√13
(c) 7/√13
(d) 5/√7
Answer
B
Question. If the straight lines x + 3y = 4, 3x + y = 4 and x + y = 0 form a triangle, then the triangle is
(a) scalene
(b) equilateral triangle
(c) isosceles
(d) right angled isosceles
Answer
C
Question. Let P = (–1, 0), Q = (0, 0) and R = (3, 3 3 ) be three point. The equation of the bisector of the angle PQR is
(a) (√3/2)x + y = 0
(b) x + √3y = 0
(c) √3x + y = 0
(d) x + (√3/2)y = 0
Answer
C
Question. If x1, x2 , x3 and y1, y2 , y3 are both in G.P. with the same common ratio, then the points (x1, y1),(x2, y2) and (x3, y3)
(a) are vertices of a triangle
(b) lie on a straight line
(c) lie on an ellipse
(d) lie on a circle.
Answer
B
Question. If A (2, – 3) and B (– 2, 1) are two vertices of a triangle and third vertex moves on the line 2x + 3y = 9, then the locus of the centroid of the triangle is :
(a) x – y =1
(b) 2x + 3y =1
(c) 2x + 3y = 3
(d) 2x – 3y = 1
Answer
B
Question. If 2 (a,a2) falls inside the angle made by the lines y = x/2, x > 0 and y = 3x , x > 0 , then a belong to
(a) (0, 1/2)
(b) (3, ∞)
(c) (1/2, 3)
(d) ( -3, – 1/2)
Answer
C
Question. The line parallel to the x- axis and passing through the intersection of the lines ax + 2by + 3b = 0 and bx – 2ay – 3a = 0, where (a, b) ≠ (0, 0) is
(a) below the x – axis at a distance of 3/2 from it
(b) below the x – axis at a distance of 2/3 from it
(c) above the x – axis at a distance of 3/2 from it
(d) above the x – axis at a distance of 2/3 from it
Answer
A
Question. The equation of the straight line passing through the point (4, 3) and making intercepts on the co-ordinate axes whose sum is –1 is
(a) x/2 – y/3 = 1 and x/–2 + y/1 = 1
(b) x/2 – y/3 = –1 and x/–2 + y/1 = –1
(c) x/2 + y/3 = 1 and x/–2 + y/1 = 1
(d) x/2 + y/3 = –1 and x/–2 + y/1 = –1
Answer
A
Question. The lines x + y = |a| and ax – y = 1 intersect each other in the first quadrant. Then the set of all possible values of a in the interval :
(a) (0,∞)
(b) [1,∞)
(c) (-1,∞)
(d) (-1,1)
Answer
B
Question. The lines L1 : y – x = 0 and L2 : 2x + y = 0 intersect the line L3 : y + 2 = 0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R.
Statement-1: The ratio PR : RQ equals 2√2: √5
Statement-2: In any triangle, bisector of an angle divides the triangle into two similar triangles.
(a) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
(b) Statement-1 is true, Statement-2 is false.
(c) Statement-1 is false, Statement-2 is true.
(d) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Answer
B
Question. Let A(2, – 3) and B(-2, 3) be vertices of a triangle ABC. If the centroid of this triangle moves on the line 2x + 3y = 1, then the locus of the vertex C is the line
(a) 3x – 2y = 3
(b) 2x -3y = 7
(c) 3x + 2y = 5
(d) 2x + 3y = 9
Answer
D
Question. The pair of lines represented by 3αx2 + 5xy + (α2 – 2)y2 = 0 are perpendicular to each other for
(a) two values of α
(b) ∀ α
(c) for one value of α
(d) for no values of α
Answer
A
Question. If one of the lines given by 6x2 – xy + 4cy2 = 0 is 3x + 4y = 0, then c equals
(a) –3
(b) 1
(c) 3
(d) 1
Answer
A
Question. If the pair of lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 intersect on the y-axis then
(a) 2fgh = bg2 + ch2
(b) bg2 ≠ ch2
(c) abc = 2fgh
(d) none of these
Answer
A
Question. The locus of the mid-points of the perpendiculars drawn from points on the line, x = 2y to the line x = y is:
(a) 2x – 3y = 0
(b) 5x – 7y = 0
(c) 3x – 2y = 0
(d) 7x – 5y = 0
Answer
B
Question. The line parallel to x-axis and passing through the point of intersection of lines ax + 2by + 3b = 0 and bx – 2ay – 3a = 0, where (a, b) ≠ (0, 0) is
(a) above x-axis at a distance 2/3 from it
(b) above x-axis at a distance 3/2 from it
(c) below x-axis at a distance 3/2 from it
(d) below x-axis at a distance 2/3 from it
Answer
C
Question. If the point (1, a) lies between the straight lines x + y = 1 and 2(x + y) = 3 then a lies in interval
(a) (3/2, ∞)
(b) (1, 3/2)
(c) (–∞, 0)
(d) (0, 1/2)
Answer
D
Question. A straight line L at a distance of 4 units from the origin makes positive intercepts on the coordinate axes and the perpendicular from the origin to this line makes an angle of 60o with the line x + y = 0. Then an equation of the line L is:
(a) x + √3y = 8
(b) (√3 +1)x + (√3 -1) y = 8√2
(c) √3x + y = 8
(d) None of these
Answer
B
Question. Lines are drawn parallel to the line 4x – 3y + 2 = 0, at a distance 3/5 from the origin. Then which one of the following points lies on any of these lines ?
(a) (– 1/4, 2/3)
(b) (1/4, 1/3)
(c) (1/4, 1/3)
(d) ( – 1/4, – 2/3)
Answer
A
Question. If the two lines x + (a–1) y = 1 and 2x + a2y =1 (a ∈ R – {0,1}) are perpendicular, then the distance of their point of intersection from the origin is:
(a) √(2/5)
(b) 2/5
(c) 2/√5
(d) √2/5
Answer
A
Question. If two vertices of a triangle are (5, –1) and (–2, 3) and its orthocentre is at (0, 0), then the third vertex is
(a) (4, – 7)
(b) (– 4, – 7)
(c) (– 4, 7)
(d) (4, 7)
Answer
B
Question. If a triangle has its orthocenter at (1, 1) and circum centre at (3/2 , 3/4) and if centroid and nine point centre are (α,β) and (γ ,δ ) respectively, then the value of 6α +12β +4γ +8δ must be:
Answer
30
Question. If m1 and m2 are the roots of the equation x2 + (√3 + 2)x + (√3 −1) = 0 and if area of the triangle formed by the lines 1 2 2 y = m x, y = m x , and y = c is (a + b)c2 , then the value of 2008 (a2 + b2 )must be:
Answer
5222
Question. If (λ, 2) is an interior point of △ABC formed by x + y = 4, 3x − 7 y = 8 and 4x − y = 31 then λ ∈(a, b), the value of 6a +8b must be:
Answer
110
Question. Consider the two lines L1 ≡ x − y = 0 and L2 ≡ x + y = 0 and a moving point (x, y).Let (P , L), i =1, 2 represents the distance of the point ‘P’ from . Li If point ‘P’ moving in certain region ‘R’ in such a way
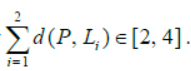
If the area of region ‘R’ is λ sq unit then the value of λ must be:
Answer
24
Question. P1.. P2.. P3..,… pn are points on the line y = x lying in the positive quadrant such that OPn/OPn−1 = n, o being the origin. If 1 OP =1 then the coordinates of 8 P are (3a√2, 3a√2), then the value of a must be:
Answer
6720
Question. If the area of the triangle formed by the lines y2 –9xy +18×2 = 0 and y = 9 is λ sq unit, then the value of 4λ must be:
Answer
27
Question. If the angle between the pair of straight lines y2 sin2θ − xy , sin2θ + x (cos2θ −1) = 0 is φ, then the value of 3 sin φ + 32sinφ + 9 must be:
Answer
42
Question. Equation ax3 − 9x2y − xy2 +4y3 = 0 represents three straight lines. If the two of the lines are perpendicular, then a – a2 must be:
Answer
20
Question. The value of λ for which the equation 12x2 – 10xy + 2y2 + 11x – 5y + λ = 0 represent a pair of straight lines, must be:
Answer
2
Question. The lines joining the origin to the common points of (x − 3)2 + ( y − 4)2 = c and 4x + 3y = 24 are at right angles, then the value of c2 must be:
Answer
25