Binomial Theorem VBQs Class 11 Mathematics

VBQs Binomial Theorem Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Binomial Theorem Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.

Binomial Theorem VBQs Class 11 Mathematics

Question. Let (x + 10)⁵⁰ + (x – 10)⁵⁰ = a₀ + a₁x + a₂x² + …. + a₅₀x⁵⁰, for all x ∈ R; then a₂/a₀ is equal to :
(a) 12.50
(b) 12.00
(c) 12.25
(d) 12.75

Question. If the third term in the binomial expansion of (1 + x^log₂x)⁵ equals 2560, then a possible value of x is:
(a) 1/4
(b) 4√2
(c) 1/8
(d) 2√2

Question. The number of terms in the expansion of (1 + x)¹⁰¹ (1 + x² – x)100 in powers of x is:
(a) 302
(b) 301
(c) 202
(d) 101

Question. If for positive integers r > 1, n > 2, the coefficients of the (3r)^th and (r + 2)^th powers of x in the expansion of (1 + x)²ⁿ are equal, then n is equal to : 
(a) 2r + 1
(b) 2r –1
(c) 3r
(d) r + 1

Question. If the fourth term in the Binomial expansion of (2/x + x^log₈x)⁶ (x > 0) is 20 × 8⁷, then a value of x is:
(a) 8³
(b) 8²
(c) 8
(d) 8^–2

Question. If the fourth term in the binomial expansion of

 is equal to 200, and x > 1, then the value of x is:
(a) 100
(b) 10
(c) 10³
(d) 10⁴

Question. The positive value of l for which the co-efficient of x2 in the expression x²(√x + λ/x²)¹⁰ is 720, is:
(a) 4
(b) 2√2
(c) √5
(d) 3

Question. If the fractional part of the number 2⁴⁰³/15 is k/15 , then k is equal to: 
(a) 6
(b) 8
(c) 4
(d) 14

Question. The natural number m, for which the coefficient of x in the binomial expansion of (x^m + 1/x²)²² is 1540, is ______.

Question. If n is the degree of the polynomial,

and m is the coefficient of xn in it, then the ordered pair (n, m) is equal to 
(a) (12 , (20)⁴)
(b) (8, 5 (10)⁴)
(c) (24 , (10)⁸)
(d) (12, 8 (10)⁴)

Question. If α and β be the coefficients of x⁴ and x² respectively in the expansion of (x + √(x² – 1))⁶ + (x – √(x² – 1))⁶ , then:
(a) α + β = 60
(b) α + β = –30
(c) α – β= 60
(d) α – β = –132

Question. If {4n – 3n – 1 : n ∈ N } and Y = {9(n -1) : nε N}, where N is the set of natural numbers, then X ∪ Y is equal to:
(a) X
(b) Y
(c) N
(d) Y – X

Question. The coefficient of x² in the expansion of the product (2 – x²). ((1 + 2x + 3x²)6 + (1 – 4x²)6) is
(a) 106
(b) 107
(c) 155
(d) 108

Question. If (27)⁹⁹⁹ is divided by 7, then the remainder is :
(a) 1
(b) 2
(c) 3
(d) 6

Question. Statement – 1 : For each natural number n, (n + 1)⁷–1 is divisible by 7.
Statement – 2 : For each natural number n, n⁷ – n is divisible by 7.
(a) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(b) Statement-1 is true, Statement-2 is true; Statement-2 is NOT a correct explanation for Statement-1
(c) Statement-1 is true, Statement-2 is false
(d) Statement-1 is false, Statement-2 is true

Question. In the expansion of (x/cosθ + 1/sinθ)¹⁶, if l₁ is the least value of the term independent of x when π/8 ≤ 0 ≤ π/4 and l₂ is the least value of the term independent of x when π/16 ≤ 0 ≤ π/8 , then the ratio l₂ : l₁ is equal to :
(a) 1 : 8
(b) 16 : 1
(c) 8 : 1
(d) 1 : 16

Question. The number of integral terms in the expansion of (√3 + ⁸√5)²⁵⁶ is
(a) 35
(b) 32
(c) 33
(d) 34

Question. If the constant term in the binomial expansion of

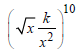
is 405, then |k| equals:
(a) 9
(b) 1
(c) 3
(d) 2

Question. If for some positive integer n, the coefficients of three consecutive terms in the binomial expansion of (1 + x)ⁿ⁺⁵ are in the ratio 5 : 10 : 14, then the largest coefficient in this expansion is :
(a) 462
(b) 330
(c) 792
(d) 252

Question. In the binomial expansion of (a – b)ⁿ, n ≥ 5, the sum of 5th and 6th terms is ero, then a/b equals
(a) (n – 5) / 6
(b) (n – 4) / 5
(c) 5/ (n – 4)
(d) 6/ (n – 5)

Question. For natural numbers m, n if (1 – y)^m (1 + y)ⁿ = 1+ a₁y + a₂y² + ……. and a₁ = a₂ = 10, then (m,n) is
(a) (20, 45)
(b) (35, 20)
(c) (45, 35)
(d) (35, 45)

Question. If the number of integral terms in the expansion of (3^1/2 + 5^1/8)ⁿ is exactly 33, then the least value of n is :
(a) 264
(b) 128
(c) 256
(d) 248

Question. The total number is irrational terms in the binomial expansion of (7^1/5 – 3^1/10)⁶⁰ is :
(a) 55
(b) 49
(c) 48
(d) 54

Question. The coefficient of x¹⁸ in the product (1+x)(1–x)¹⁰ (1+x+x²)⁹ is :
(a) 84
(b) –126
(c) –84
(d) 126

Question. The ratio of the coefficient of x¹⁵ to the term independent of x in the expansion of (x² + 2/x)¹⁵ is :
(a) 7 : 16
(b) 7 : 64
(c) 1 : 4
(d) 1 : 32

Question. The middle term in the expansion of (1 – 1/x)n (1 – x)n in power of x is
(a) ^–2nC_n–1
(b) ^{– 2}nCn
(c) ²ⁿC_n–1
(d) 2nC_n

Question. If x is so small that x³ and higher powers of x may be neglected, then

 may be approximated as
(a) 1 – 3/8 x²
(b) 3x + 3/8 x²
(c) – 3/8 x²
(d) x/2 – 3/8 x²

Question. If x is positive, the first negative term in the expansion of (1+ x)^27/5 is
(a) 6th term
(b) 7th term
(c) 5th term
(d) 8th term

Question. The coefficient of the middle term in the binomial expansion in powers of x of (1+ αx)⁴ and of (1 – αx)⁶ is the same if
α equals
(a) 3/5
(b) 10/3
(c) -3/10
(d) -5/3

Question. A ratio of the 5th term from the begining to the 5th term from the end in the binomial expansion of (2^1/3 + 1/2(3)^1/3)¹⁰ is:
(a) 1 : 2(6)^1/3
(b) 1/1 : 4(16)^1/3
(c) 4(36)^1/3 : 1
(d) 2(36)^1/3 : 1

Question. If ²⁰C₁ + (2²) ²⁰C₂ +(3²) ²⁰C₃+ ………. + (20²) ²⁰C₂₀ = A(2^β), then the ordered pair (A, β) is equal to :
(a) (420, 19)
(b) (420, 18)
(c) (380, 18)
(d) (380, 19)

Question.

Statement – 1 : S₃ = 55 × 2⁹.
Statement – 2 : S₁ = 90 × 2⁸ and S₂ = 10 × 2⁸.
(a) Statement -1 is true, Statement -2 is true ; Statement – 2 is not a correct explanation for Statement -1.
(b) Statement -1 is true, Statement -2 is false.
(c) Statement -1 is false, Statement -2 is true .
(d) Statement – 1 is true, Statement 2 is true ; Statement -2 is a correct explanation for Statement -1.

Question. In a shop there are five types of ice-creams available. A child buys six ice-creams.
Statement – 1 : The number of different ways the child can buy the six ice-creams is ¹⁰C₅.
Statement – 2 : The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row.
(a) Statement -1 is false, Statement-2 is true
(b) Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
(c) Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
(d) Statement -1 is true, Statement-2 is false

Question. The value of

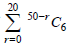
 is equal to :
(a) ⁵¹C₇ – ³⁰C₇
(b) ⁵⁰C₇ – ³⁰C₇
(c) ⁵⁰C₆ – ³⁰C₆
(d) ⁵¹C₇ + ³⁰C₇

Question. The term independent of x in the expansion of (1/60 – x⁸/81) · (2x² – 3/x²)⁶ is equal to :
(a) –72
(b) 36
(c) –36
(d) –108

Question. The coefficient of x7 in the expansion of (1– x – x² + x³ )⁶ is
(a) –132
(b) –144
(c) 132
(d) 144

Question. If the coefficients of x^–2 and x^–4 in the expansion of

(x > 0), are m and n respectively, then m/n is equal to : 
(a) 27
(b) 182
(c) 5/4
(d) 4/5

Question. The remainder left out when 8²ⁿ – (62)²ⁿ⁺¹ is divided by 9 is:
(a) 2
(b) 7
(c) 8
(d) 0

Question. The coefficient of x10 in the expansion of (1 + x)² (1 + x2)³ (1 + x3)4 is equal to
(a) 52
(b) 44
(c) 50
(d) 56

Question. If {p} denotes the fractional part of the number p, then {3²⁰⁰/8}, is equal to :
(a) 5/8
(b) 7/8
(c) 3/8
(d) 1/8

Question.

(a) Statement -1 is false, Statement-2 is true
(b) Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
(c) Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
(d) Statement -1 is true, Statement-2 is false

Question. If the coefficients of the three successive terms in the binomial expansion of (1 + x)n are in the ratio 1 : 7 : 42, then the first of these terms in the expansion is:
(a) 8th
(b) 6th
(c) 7th
(d) 9th

Question. If some three consecutive coefficients in the binomial expansion of (x + 1)ⁿ in powers of x are in the ratio 2:15:70, then the average of these three coefficients is:
(a) 964
(b) 232
(c) 227
(d) 625

Question. The sum of the co-efficients of all even degree terms in x in the expansion of (x + √(x³-1))⁶ + (x – √(x³-1))⁶ , (x > 1) is equal to :
(a) 29
(b) 32
(c) 26
(d) 24

Question. If the coefficents of x3 and x4 in the expansion of (1+ ax + bx²) (1- 2x)¹⁸ in powers of x are both ero, then
(a, b) is equal to:
(a) (14 , 272/3)
(b) (16 , 272/3)
(c) (16 , 251/3)
(d) (14 , 251/3)

Question. Let

 Then a₇ / a₁₃ is equal to ___________.

Question.

(a) – 4
(b) 6
(c) – 8
(d) 10

Question. If the 7th term in the binomial expansion of

 is equal to 729, then x can be :
(a) e²
(b) e
(c) e/2
(d) 2e

Question. If n is a positive integer, then (√3+1)²ⁿ – (√3 –1)²ⁿ is :
(a) an irrational number
(b) an odd positive integer
(c) an even positive integer
(d) a rational number other than positive integers

Question. If (2+x/3)⁵⁵ is expanded in the ascending powers of x and the coefficients of powers of x in two consecutive terms of the expansion are equal, then these terms are:
(a) 7th and 8th
(b) 8th and 9th
(c) 28th and 29th
(d) 27th and 28th

Question. The sum of the rational terms in the binomial expansion of (2^1/2 + 3^1/5)¹⁰ is :
(a) 25
(b) 32
(c) 9
(d) 41

Question. The coefficient of x⁴ in the expansion of (1 + x + x² + x³)⁶ in powers of x, is ____________.

Question. The smallest natural number n, such that the coefficient of x in the expansion of (x² + 1/x³)ⁿ is ⁿC₂₃, is :
(a) 38
(b) 58
(c) 23
(d) 35

Question. The number of terms in the expansion of (y^1/5 + x^1/10)⁵⁵ , in which powers of x and y are free from radical signs are
(a) six
(b) twelve
(c) seven
(d) five

Question. If ƒ(y) = 1 – (y – 1) + (y – 1)² – (y – 1)³ + … – (y – 1)¹⁷, then the coefficient of y² in it is
(a) 17C₂
(b) 17C₃
(c) 18C₂
(d) 18C₃

Question. The sum of the co-efficients of all odd degree terms in the expansion of (x+ √x³–1) + (x– √x³ -1) ,(x >1) is :
(a) 0
(b) 1
(c) 2
(d) – 1

Question. The coefficient of x^–5 in the binomial expansion of

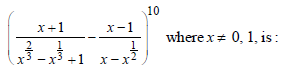
(a) 1
(b) 4
(c) – 4
(d) – 1

Question. If the coefficients of x² and x³ are both ero, in the expansion of the expression (1 + ax + bx²) (1–3x)¹⁵ in powers of x, then the ordered pair (a, b) is equal to:
(a) (28, 861)
(b) (–54, 315)
(c) (28, 315)
(d) (–21, 714)

Question. If the coefficient of x⁷ in [ ax² + (1/bx) ]¹¹ equals the coefficient of x⁷ in [ ax – (1/bx) ]¹¹ , then a and b satisfy the relation
(a) a – b = 1
(b) a + b = 1
(c) a/b = 1
(d) ab = 1

Question. For a positive integer n, (1 + 1/x)ⁿ is expanded in increasing powers of x. If three consecutive coefficients in this expansion are in the ratio, 2 : 5 : 12, then n is equal to __________.

Question. The coefficient of xⁿ in expansion of (1 + x)(1 – x)ⁿ is
(a) ( –1)^n–1n
(b) ( – 1)ⁿ(1 – n)
(c) ( – 1)^n–1(n – 1)²
(d) (n – 1)

Question. The sum of the series 2 · ²⁰C₀ + 5 · ²⁰C₁ + 8 · ²⁰C₂ + 11 · ²⁰C₃ + … + 62 · ²⁰C20 is equal to :
(a) 2²⁶
(b) 2²⁵
(c) 2²³
(d) 2²⁴

Question. If the sum of the coefficients in the expansion of (a + b)ⁿ is 4096, then the greatest coefficient in the expansion is
(a) 1594
(b) 792
(c) 924
(d) 2924

Question. The coefficient of t⁴ in the expansion of ( 1 – t⁶ / 1 – t )³
(a) 14
(b) 15
(c) 10
(d) 12

Question. The sum of the real values of x for which the middle term in the binomial expansion of (x³/3 + 3/x)⁸ equals 5670 is :
(a) 0
(b) 6
(c) 4
(d) 8

Question. If the term independent of x in the expansion of

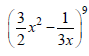
 is k, then 18k is equal to :
(a) 5
(b) 9
(c) 7
(d) 11

Question. If the number of terms in the expansion of ( 1 – 2/x + 4/x² )ⁿ , x ≠ 0, is 28, then the sum of the coefficients of all the terms in this expansion, is :
(a) 243
(b) 729
(c) 64
(d) 2187

Question. The sum of coefficients of integral power of x in the binomial expansion (1–2√x)⁵⁰ is :
(a) 1/2(3⁵⁰ – 1)
(b) 1/2(2⁵⁰ – 1)
(c) 1/2(3⁵⁰ + 1)
(d) 1/2(3⁵⁰)

Question. Let α > 0, β > 0 be such that α³ +β² = 4. If the maximum value of the term independent of x in the binomial expansion of (αx^1/9 + βx^1/6)¹⁰ is 10k, then k is equal to :
(a) 336
(b) 352
(c) 84
(d) 176

Question. The value of r for which ²⁰C_r²⁰C₀ + ²⁰C_r-1²⁰C₁ + ²⁰C_r-2²⁰C₂ + … +²⁰C₀²⁰C_r is maximum, is :
(a) 15
(b) 20
(c) 11
(d) 10

Question. If

 then K is equal to:
(a) (25)²
(b) 2²⁵ – 1
(c) 2²⁴
(d) 2²⁵

Question. The positive integer ust greater than (1 + 0.0001)¹⁰⁰⁰⁰ is
(a) 4
(b) 5
(c) 2
(d) 3

Question. The value of (²¹C₁ – ¹⁰C₁) + (²¹C₂ – ¹⁰C₂) + (²¹C₃ – ¹⁰C₃) + (²¹C₄ – ¹⁰C₄) + …. + (²¹C₁₀ – ¹⁰C₁₀) is :
(a) 2²⁰ – 2¹⁰
(b) 2²¹ – 2¹¹
(c) 2²¹ – 2¹⁰
(d) 2²⁰ – 2⁹

Question. The coefficient of x¹⁰¹² in the expansion of (1 + xⁿ + x²⁵³)¹⁰, (where n ≤ 22 is any positive integer), is
(a) 1
(b) ¹⁰C₄
(c) 4n
(d) ²⁵³C₄

Question. The sum of the series ²⁰C₀ – ²⁰C₁ + ²⁰C₂ – ²⁰C₃ + …. – …. + ²⁰c₁₀ is
(a) 0
(b) ²⁰C₁₀
(c) – ²⁰C₁₀
(d) 1/2²⁰C₁₀

Question. r and n are positive integers r > 1, n > 2 and coefficient of (r+2)^th term and 3r^th term in the expansion of (1 + x)²ⁿ are equal, then n equals
(a) 3r
(b) 3r + 1
(c) 2r
(d) 2r + 1

Question. The coefficients of x^p and x^q in the expansion of (1+ x )^p+q are
(a) equal
(b) equal with opposite signs
(c) reciprocals of each other
(d) none of these

Question. The coefficient of x4 in the expansion of (1 + x + x²)¹⁰ is _______.

Question. If the sum of the coefficients of all even powers of x in the product (1 + x + x² + … + x²ⁿ) (1 – x + x² – x³ + … + x²ⁿ) is 61, then n is equal to_______.

Question. The term independent of x in the binomial expansion of (1 – 1/x + 3x⁵)(2x² – 1/X)⁸ is :
(a) 496
(b) –496
(c) 400
(d) –400

Question. The term independent of x in expansion of

(a) 4
(b) 120
(c) 210
(d) 310