VBQs Permutations and Combinations Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Permutations and Combinations Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Permutations and Combinations VBQs Class 11 Mathematics
Question. The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by
(a) 6! × 5!
(b) 6 × 5
(c) 30
(d) 5 × 4
Answer
A
Question. The sum of integers from 1 to 100 that are divisible by 2 or 5 is
(a) 3000
(b) 3050
(c) 3600
(d) 3250
Answer
B
Question. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is :
(a) less than 500
(b) at least 500 but less than 750
(c) at least 750 but less than 1000
(d) at least 1000
Answer
D
Question. A man X has 7 friends, 4 of them are ladies and 3 are men. His wife Y also has 7 friends, 3 of them are ladies and 4 are men. Assume X and Y have no common friends. Then the total number of ways in which X and Y together can throw a party inviting 3 ladies and 3 men, so that 3 friends of each of X and Y are in this party, is :
(a) 484
(b) 485
(c) 468
(d) 469
Answer
B
Question. Total number of 6-digit numbers in which only and all the five digits 1, 3, 5, 7 and 9 appear, is:
(a) 1/2 (6!)
(b) 6!
(c) 56
(d) 5/2 (6!)
Answer
D
Question. Let S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 sq. units, then the number of elements in the set S is:
(a) 9
(b) 18
(c) 36
(d) 32
Answer
C
Question. If
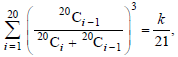
then k equals:
(a) 400
(b) 50
(c) 200
(d) 100
Answer
D
Question. Consider a class of 5 girls and 7 boys. The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys A and B, who refuse to be the members of the same team, is:
(a) 500
(b) 200
(c) 300
(d) 350
Answer
C
Question. The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4, (repetition of digits is not allowed) and are multiple of 3 is?
(a) 30
(b) 48
(c) 24
(d) 36
Answer
A
Question. If all the words, with or without meaning, are written using the letters of the word QUEEN and are arranged as in English dictionary, then the position of the word QUEEN is :
(a) 44th
(b) 45th
(c) 46th
(d) 47th
Answer
C
Question. If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is :
(a) 52nd
(b) 58th
(c) 46th
(d) 59th
Answer
B
Question. Two families with three members each and one family with four members are to be seated in a row. In how many ways can they be seated so that the same family members are not separated?
(a) 2! 3! 4!
(b) (3!)3 × (4!)
(c) (3!)2 × (4!)
(d) 3! (4!)3
Answer
B
Question. The value of (2× 1P0 -3 · 2P1 + 4· 3P2 – … up to 51th term) + (1! – 2! + 3! – … up to 51th term) is equal to :
(a) 1 – 51(51)!
(b) 1 + (51)!
(c) 1 + (52)!
(d) 1
Answer
C
Question. The sum
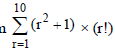
is equal to :
(a) 11 × (11!)
(b) 10 × (11!)
(c) (11!)
(d) 101 × (10!)
Answer
B
Question. The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is :
(a) 120
(b) 72
(c) 216
(d) 192
Answer
D
Question. Let n > 2 be an integer. Suppose that there are n Metro stations in a city located along a circular path. Each pair of stations is connected by a straight track only. Further, each pair of nearest stations is connected by blue line, whereas all remaining pairs of stations are connected by red line. If the number of red lines is 99 times the number of blue lines, then the value of n is :
(a) 201
(b) 200
(c) 101
(d) 199
Answer
A
Question. If Cr ≡ 25Cr and C0 + 5×C1 + 9 · C2 + … + (101) · C25 = 225 · k, then k is equal to ________.
Answer
51
Question. The number of ways of selecting 15 teams from 15 men and 15 women, such that each team consists of a man and a woman, is:
(a) 1120
(b) 1880
(c) 1960
(d) 1240
Answer
D
Question. A committee of 11 members is to be formed from 8 males and 5 females. If m is the number of ways the committee is formed with at least 6 males and n is the number of ways the committee is formed with at least 3 females, then:
(a) m + n = 68
(b) m = n = 78
(c) n = m – 8
(d) m = n = 68
Answer
B
Question. All possible numbers are formed using the digits 1, 1, 2, 2, 2, 2, 3, 4, 4 taken all at a time. The number of such numbers in which the odd digits occupy even places is :
(a) 180
(b) 175
(c) 160
(d) 162
Answer
A
Question. Two women and some men participated in a chess tournament in which every participant played two games with each of the other participants. If the number of games that the men played between themselves exceeds the number of games that the men played with the women by 66, then the number of men who participated in the tournament lies in the interval:
(a) [8, 9]
(b) [10, 12)
(c) (11, 13]
(d) (14, 17)
Answer
B
Question. There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is
(a) 36
(b) 66
(c) 108
(d) 3
Answer
C
Question. From 6 different novels and 3 different dictionaries,4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then the number of such arrangement is:
(a) at least 500 but less than 750
(b) at least 750 but less than 1000
(c) at least 1000
(d) less than 500
Answer
C
Question. 8-digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do no occupy odd places, is:
(a) 160
(b) 120
(c) 60
(d) 48
Answer
B
Question. 5 – digit numbers are to be formed using 2, 3, 5, 7, 9 without repeating the digits. If p be the number of such numbers that exceed 20000 and q be the number of those that lie between 30000 and 90000, then p : q is :
(a) 6 : 5
(b) 3 : 2
(c) 4 : 3
(d) 5 : 3
Answer
D
Question. If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number
(a) 601
(b) 600
(c) 603
(d) 602
Answer
A
Question. Consider three boxes, each containing 10 balls labelled 1, 2,…, 10. Suppose one ball is randomly drawn from each of the boxes. Denote by ni, the label of the ball drawn from the ith box, (i = 1, 2, 3). Then, the number of ways in which the balls can be chosen such that n1 < n2 < n3 is :
(a) 120
(b) 82
(c) 240
(d) 164
Answer
A
Question. The number of natural numbers less than 7,000 which can be formed by using the digits 0,1,3,7,9 (repetition of digits allowed) is equal to:
(a) 374
(b) 372
(c) 375
(d) 250
Answer
A
Question. How many ways are there to arrange the letters in the word GARDEN with vowels in alphabetical order
(a) 480
(b) 240
(c) 360
(d) 120
Answer
C
Question. The set S = {1, 2, 3, ……., 12} is to be partitioned into three sets A, B, C of equal size. Thus A ∪ B ∪ C = S, A ∩ B = B ∩ C = A ∩ C = Φ. The number of ways to partition S is
(a) 12! / (4!)3
(b) 12! / (4!)4
(c) 12! / 3!(4!)3
(d) 12! / 3!(4!)4
Answer
A
Question. At an election, a voter may vote for any number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are of be selected, if a voter votes for at least one candidate, then the number of ways in which he can vote is
(a) 5040
(b) 6210
(c) 385
(d) 1110
Answer
C
Question. The range of the function ƒ(x) = 7-xPx-3 is
(a) {1, 2, 3, 4, 5}
(b) {1, 2, 3, 4, 5, 6}
(c) {1, 2, 3, 4,}
(d) {1, 2, 3,}
Answer
D
Question. Number greater than 1000 but less than 4000 is formed using the digits 0, 1, 2, 3, 4 (repetition allowed). Their number is
(a) 125
(b) 105
(c) 374
(d) 625
Answer
C
Question. The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
(a) 8C3
(b) 21
(c) 38
(d) 5
Answer
B
Question. A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
(a) 346
(b) 140
(c) 196
(d) 280
Answer
C
Question. Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 5, 7 (using repetition allowed) are
(a) 216
(b) 375
(c) 400
(d) 720
Answer
D
Question. The number of words (with or without meaning) that can be formed from all the letters of the word “LETTER” in which vowels never come together is ______.
Answer
120.00
Question. A test consists of 6 multiple choice questions, each having 4 alternative answers of which only one is correct. The number of ways, in which a candidate answers all six questions such that exactly four of the answers are correct, is __________.
Answer
135
Question. The number of 6 digit numbers that can be formed using the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11 and no digit is repeated, is:
(a) 72
(b) 60
(c) 48
(d) 36
Answer
B
Question. The number of four-digit numbers strictly greater than 4321 that can be formed using the digits 0, 1, 2, 3, 4, 5 (repetition of digits is allowed) is:
(a) 288
(b) 360
(c) 306
(d) 310
Answer
D
Question. The total number of 3-digit numbers, whose sum of digits is 10, is _________.
Answer
54
Question. An urn contains 5 red marbles, 4 black marbles and 3 white marbles. Then the number of ways in which 4 marbles can be drawn so that at the most three of them are red is _________.
Answer
490
Question. An eight digit number divisible by 9 is to be formed using digits from 0 to 9 without repeating the digits. The number of ways in which this can be done is:
(a) 72 (7!)
(b) 18 (7!)
(c) 40 (7!)
(d) 36 (7!)
Answer
D
Question. The sum of the digits in the unit’s place of all the 4-digit numbers formed by using the numbers 3, 4, 5 and 6, without repetition, is:
(a) 432
(b) 108
(c) 36
(d) 18
Answer
B
Question. If a, b and c are the greatest values of 19Cp, 20Cq and 21Cr respectively, then:
(a) a/11 = b/22 = c/21
(b) a/10 = b/11 = c/21
(c) a/11 = b/22 = c/42
(d) a/10 = b/11 = c/42
Answer
C
Question. If the four letter words (need not be meaningful) are to be formed using the letters from the word “MEDITERRANEAN” such that the first letter is R and the fourth letter is E, then the total number of all such words is :
(a) 110
(b) 59
(c) 11!/(2!)3
(d) 56
Answer
C
Question. Let A and B be two sets containing four and two elements respectively. Then the number of subsets of the set A × B, each having at least three elements is :
(a) 275
(b) 510
(c) 219
(d) 256
Answer
C
Question. If in a regular polygon the number of diagonals is 54, then the number of sides of this polygon is
(a) 12
(b) 6
(c) 10
(d) 9
Answer
A
Question. The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0, 0), (0, 41) and (41, 0) is :
(a) 820
(b) 780
(c) 901
(d) 861
Answer
B
Question. The number of 4 letter words (with or without meaning) that can be formed from the eleven letters of the word ‘EXAMINATION’ is _________.
Answer
2454
Question. The number of ordered pairs (r, k) for which 6.35Cr = (k2 – 3).36Cr+1, where k is an integer, is:
(a) 3
(b) 2
(c) 6
(d) 4
Answer
D
Question. Statement 1: If A and B be two sets having p and q elements respectively, where q > p. Then the total number of functions from set A to set B is qp.
Statement 2: The total number of selections of p different ob ects out of q ob ects is qCp.
(a) Statement 1 is true, Statement 2 is false.
(b) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation of Statement 1.
(c) Statement 1 is false, Statement 2 is true
(d) Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation of Statement 1.
Answer
D
Question. If the number of 5-element subsets of the set A= {a1, a2, …., a20} of 20 distinct elements is k times the number of 5-element subsets containing a4, then k is
(a) 5
(b) 20/7
(c) 4
(d) 10/3
Answer
C
Question. The number of ways of choosing 10 ob ects out of 31 ob ects of which 10 are identical and the remaining 21 are distinct is:
(a) 220–1
(b) 221
(c) 220
(d) 220+1
Answer
C
Question. There are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then the value of m is
(a) 12
(b) 11
(c) 9
(d) 7
Answer
A
Question. The number of four letter words that can be formed using the letters of the word BARRACK is
(a) 144
(b) 120
(c) 264
(d) 270
Answer
D
Question. If n+2C6 / n-2P2 = 11, then n satisfies the equation :
(a) n2 + n – 110 = 0
(b) n2 + 2n – 80 = 0
(c) n2 + 3n – 108 = 0
(d) n2 + 5n – 84 = 0
Answer
C
Question. The value of
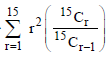
is equal to :
(a) 1240
(b) 560
(c) 1085
(d) 680
Answer
D
Question. Let A and B two sets containing 2 elements and 4 elements respectively. The number of subsets of A × B having 3 or more elements is
(a) 256
(b) 220
(c) 219
(d) 211
Answer
C
Question. If nCr denotes the number of combination of n things taken r at a time, then the expression nCr+1 + nCr-1 + 2 × nCr equals
(a) n+1Cr+1
(b) n+2Cr
(c) n+2Cr+1
(d) n+1Cr
Answer
C
Question. Five digit number divisible by 3 is formed using 0, 1, 2, 3, 4, 6 and 7 without repetition. Total number of such numbers are
(a) 312
(b) 3125
(c) 120
(d) 216
Answer
D
Question. Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 – Tn = 10, then the value of n is :
(a) 7
(b) 5
(c) 10
(d) 8
Answer
B
Question. The number of words, with or without meaning, that can be formed by taking 4 letters at a time from the letters of the word ‘SYLLABUS’ such that two letters are distinct and two letters are alike, is ______.
Answer
240
Question. There are 3 sections in a question paper and each section contains 5 questions. A candidate has to answer a total of 5 questions, choosing at least one question from each section. Then the number of ways, in which the candidate can choose the questions, is :
(a) 3000
(b) 1500
(c) 2255
(d) 2250
Answer
D
Question. On the sides AB, BC, CA of a ΔABC, 3, 4, 5 distinct points (excluding vertices A, B, C) are respectively chosen. The number of triangles that can be constructed using these chosen points as vertices are :
(a) 210
(b) 205
(c) 215
(d) 220
Answer
B
Question. A group of students comprises of 5 boys and n girls. If the number of ways, in which a team of 3 students can randomly be selected from this group such that there is at least one boy and at least one girl in each team, is 1750, then n is equal to :
(a) 28
(b) 27
(c) 25
(d) 24
Answer
C
Question. Suppose that 20 pillars of the same height have been erected along the boundary of a circular stadium. If the top of each pillar has been connected by beams with the top of all its non-adjacent pillars, then the total number of beams is :
(a) 170
(b) 180
(c) 210
(d) 190
Answer
A
Question. The number of arrangements that can be formed from the letters a, b, c, d, e, f taken 3 at a time without repetition and each arrangement containing at least one vowel, is
(a) 96
(b) 128
(c) 24
(d) 72
Answer
A
Question. If the letters of the word ‘MOTHER’ be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word ‘MOTHER’ is ________.
Answer
309
Question. If the number of five digit numbers with distinct digits and 2 at the 10th place is 336 k, then k is equal to:
(a) 4
(b) 6
(c) 7
(d) 8
Answer
D
Question. If n = mC2, then the value of nC2 is given by
(a) 3(m+1C4)
(b) m–1C4
(c) m+1C4
(d) 2(m+2C4)
Answer
A
Question. Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is:
(a) 880
(b) 629
(c) 630
(d) 879
Answer
D
Question. If seven women and seven men are to be seated around a circular table such that there is a man on either side of every woman, then the number of seating arrangements is
(a) 6! 7!
(b) (6!)2
(c) (7!)2
(d) 7!
Answer
A
Question. There are 10 points in a plane, out of these 6 are collinear. If N is the number of triangles formed by oining these points. Then :
(a) N ≤ 100
(b) 100 < N ≤ 140
(c) 140 < N ≤ 190
(d) N > 190
Answer
A
Question. Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3.
Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3.
(a) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
(b) Statement-1 is true, Statement-2 is false.
(c) Statement-1 is false, Statement-2 is true.
(d) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Answer
A
Question. How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?
(a) 8. 6C4. 7C4
(b) 6.7. 8C4
(c) 6. 8. 7C4.
(d) 7. 6C4. 8C4
Answer
D
Question. The value of
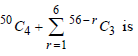
(a) 55C4
(b) 55C3
(c) 56C3
(d) 56C4
Answer
D
Question. The number of ways in which an examiner can assign 30 marks to 8 questions, giving not less than 2 marks to any question, is :
(a) 30C7
(b) 21C8
(c) 21C7
(d) 30C8
Answer
C
Question. A commit tee of 4 persons is to be formed from 2 ladies, 2 old men and 4 young men such that it includes at least 1 lady, at least 1 old man and at most 2 young men. Then the total number of ways in which this committee can be formed is :
(a) 40
(b) 41
(c) 16
(d) 32
Answer
B
Question. n – digit numbers are formed using only three digits 2, 5 and 7. The smallest value of n for which 900 such distinct numbers can be formed, is
(a) 6
(b) 8
(c) 9
(d) 7
Answer
D
Question. The number of ways in which 5 boys and 3 girls can be seated on a round table if a particular boy B1 and a particular girl G1 never sit ad adjcent to each other, is :
(a) 5 × 6!
(b) 6 × 6!
(c) 7!
(d) 5 × 7!
Answer
A