Please refer to Nuclei Class 12 Physics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Physics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Physics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.
Class 12 Physics Important Questions Nuclei
Very Short Answer Type Questions
Question. In decay of free neutron, name the elementary particle emitted along with proton and electron in nuclear reaction.
Answer. Anti-neutrino.
Question. Four nuclei of an element undergo fusion to form a heavier nucleus, with release of energy. Which of the two — the parent or the daughter nucleus — would have higher binding energy per nucleon?
Answer. Daughter nucleus
Question. The binding energies per nucleon for deutron and an alpha-particle are x1 and x2 respectively. Find the amount of energy released in the following reactions.
3H2 + 3H2 → 4HE2 + Q
Answer. 4 (x2 – x1).
Question. How the mass density of a nucleus varies with mass number ?
Answer. Mass density is independent of mass number.
Question. If the atomic number of an element is 11 and the atomic mass is 24, how many electrons does it have?
Answer. Atomic number of any element gives the number of protons which is equal to the number of electrons in an atom. Sodium has atomic number 11, this shows that Sodium atom has 11 protons in its nucleus and has 11 electrons surrounding its nucleus.
Question. What do you mean by mass defect of a nucleus?
Answer. The difference between the rest mass of a nucleus and the sum of the rest masses of its constituent nucleons is called its mass defect. It is given by
Δm = Zmp + (A – Z) mn – M 1
Question. What do you mean by binding energy per nucleon?
Answer. The binding energy per nucleon may be defined as
the energy required to break up a nucleus into its constituent protons and neutrons and to separate them to such a large distance so that they may not interact with each other. It may also be defined as the surplus energy which the nucleons give up by virtue of their attractions when they become bound together to form a nucleus.
The binding energy of a nucleus is given by
Δm = Zmp + (A – Z) mn – Mnuc
Eb = (Δm) c2
Question. On the basis of which relation mass to energy conversion in nuclear fusion and fission is explained ?
Answer. Since, Nuclear Fission and Fusion are processes in which mass is converted into energy. Hence, nuclear fission and fusion can be explained on the basis of Einstein mass-energy equivalence relation.
Question. Identify the nucleides X and Y in the nuclear reactions.
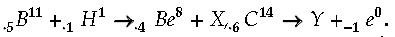
Answer. Using conservation of mass number and charge number

Short Answer Type Questions-I
Question. Calculate for how many years the fusion of 2.0 kg deuterium will keep 800 W electric lamp glowing.
Take the fusion reaction as
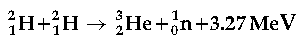
Answer. The given fusion reaction is:

Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms
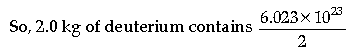
× 2000 = 6.023 × 1026 atoms
Two atoms of deuterium fuse to release 3.27 MeV energy.
So, total energy released

Power of the electric lamp, P = 800 W = 800 J/s
Hence, the energy consumed by the lamp per second = 800 J
So, the electric lamp will glow for
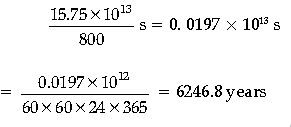
Question. A heavy nucleus P of mass number 240 and binding energy 7.6 MeV per nucleon splits in to two nuclei Q and R of mass numbers 110 and 130 and binding energy per nucleon 8.5 MeV and 8.4 MeV, respectively. Calculate the energy released in the fission.
Answer. Total BE of P = 240 × 7.6 = 1824 MeV
BE of Q = 110 × 8.5 = 935 MeV
BE of R = 130 × 8.4 = 1092 MeV
Total BE of Q and R = (935 +1092) = 2027 MeV
Total energy released in the fission
= 2027 – 1824
= 203 MeV
Question. Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A.
Answer. (a) Drawing the plot
Explaining the process of Nuclear fission and Nuclear fusion.
The plot of (B.E. / nucleon) verses mass number is as shown.
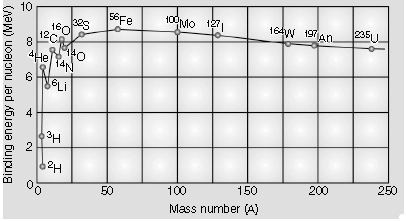
[ Note :Also accept the diagram that just shows the general shape of the graph]. From the plot we note that
(i) During nuclear fission A heavy nucleus in the larger mass region ( A>200) breaks into two middle level nuclei, resulting in an increase in B.E/ nucleon. This results in a release of energy.
(ii) During nuclear fusion Lighter nuclei in the lower mass region (A<20) fuse to form a nucleus having higher B.E. / nucleon.
Hence Energy gets released.
[Alternatively : As per the plot, during nuclear fission as well as nuclear fusion, the final value of B.E/ nucleon is more than its initial value. Hence energy gets released in both these processes. ]
Question. Calculate the energy in fusion reaction :
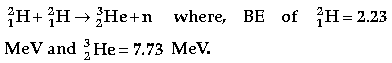
Answer. Calculation of Energy in fusion reaction
Total Binding energy of initial system
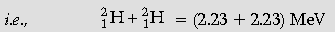
= 4.46 MeV 1
Binding energy of final system i.e., 32He
= 7.73 MeV
Hence energy released = 7.73 MeV – 4.46 MeV 1
= 3.27 MeV
Question. Show that the density of nucleus over a wide range of nuclei is constant and independent of mass number.
Answer. We have
R = R0 A1/3
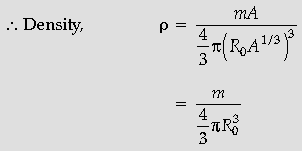
Hence r is independent of A.
(Here m is the mass of the nucleus.)
Question. A nucleus with mass number A = 240 and BE/A = 7.6 MeV breaks into two fragments each of A = 120 with BE/A = 8.5 MeV. Calculate the released energy.
Answer. Calculation of energy released Binding energy of nucleus with mass number 240,
Ebn = 240 × 7.6 MeV
Binding energy of two fragments
= 2 × 120 × 8.5 MeV
Energy released = 240(8.5 – 7.6) MeV
= 240 × 0.9
= 216 MeV
Short Answer Type Questions-II
Question. Draw the curve showing the variation of binding energy per nucleon with the mass number of nuclei. Using it explain the fusion of nuclei lying on ascending part and fission of nuclei lying on descending part of this curve.
Answer.
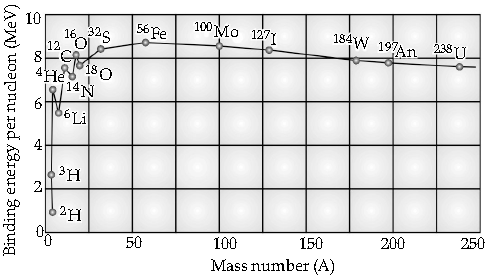
From the graph, it is clear that it has a peak near A = 60. Nuclei around this are most stable. (Example :
Iron)
The shape of this curve suggests two possibilities for converting significant amounts of mass into energy :
(i) Fission reactions: From the curve, the heaviest nuclei are less stable than the nuclei near A = 60.
This suggests that energy can be released if heavy nuclei split apart into smaller nuclei. This process is called fission.
(ii) Fusion reactions: The curve also suggests energy can be released from the lighter elements (like hydrogen and helium) as they are less stable than heavier elements up to A~60. Thus, sticking two light nuclei together to form a heavier nucleus can also release energy. This process is called fusion.
In both fission and fusion reactions, the total masses after the reaction are less than those before. This “missing mass” appears as energy.
Question. Binding energy per nucleon versus mass number curve is as shown.
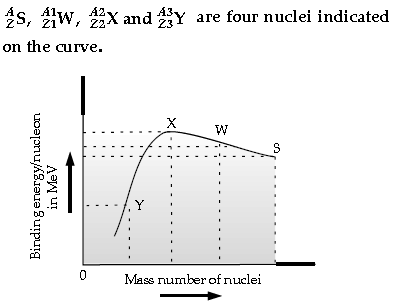
Based on the graph :
(a) Arrange X, W and S in the increasing order of stability.
(b) Write the relation between the relevant A and Z values for the following nuclear reaction.
S → X + W
(c) Explain why binding energy for heavy nuclei is low.
Answer. (a) S, W, X
(b) Z = Z1 + Z2
A = A1 + A2
(c) Reason for low binding energy : In heavier nuclei, the Coulombian repulsive effects can increase considerably and can match/offset the attractive effects of the nuclear forces. This can result in such nuclei being unstable.
Question. Distinguish between nuclear fission and fusion.
Show how in both these processes energy is released.
Calculate the energy release in MeV in the deuterium-tritium fusion reaction :

Answer. Nuclear Fission is the breaking down of heavier nucleus into smaller fragments while nuclear fusion is combining of lighter nuclei to form heavier nucleus. We see that binding energy per nucleon of daughter nuclei in both fission and fusion processes is more than that of parent nuclei. Further, the difference in binding energy is released, in form of energy while in both the processes certain masses get converted into energy.
In both processes, some mass get converted into energy.
Energy Released,

= [2.014102 + 3.016049 – 4.002603 – 1.008665]
× 931.5 MeV
= 0.018883 × 931.5 MeV
= 17.59 MeV
Question. (a) Give one point of difference between nuclear fission and nuclear fusion.
(b) Suppose we consider fission of a 2656Fe into two equal fragments of 2813Al nucleus. Is the fission
energetically possible? Justify your answer by working out Q value of the process.
Given (m) 5626Fe = 55.93494 u and (m) 2813Al = 27.98191
Answer. One difference between nuclear fission and nuclear fusion
Calculating Q = ((m) Fe – 2 (m) Al) c2
= – 26.90 MeV 1
Justification not possible
Question. (a) State two distinguishing features of nuclear force.
(b) Draw a plot showing the variation of potential energy of a pair of nucleons as a function of their separation. Mark the regions on the graph where the force is (i) attractive, and (ii) repulsive.
Answer. (a) Stating distinguishing feature of nuclear force.
(b) Draw a plot showing variation of potential energy.
(c) Marking the regions.
(a) Distinguishing feature:
(1) Short range force
(2) Strongest force
(3) Attractive in nature
(4) Does not depend on charge (any two)
(b) Plot showing variation of potential energy:

(c) Making the regions:
r < r0 : repulsive force
r > r0 : attractive force

