Please refer to MCQ Questions Chapter 8 Trigonometry Class 10 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 10 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 10 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 8 Trigonometry in Class 10 Mathematics provided below to get more marks in exams.
Chapter 8 Trigonometry MCQ Questions
Please refer to the following Chapter 8 Trigonometry MCQ Questions Class 10 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 8 Trigonometry Class 10 Mathematics
Question. Select the equation represented by the graph below.
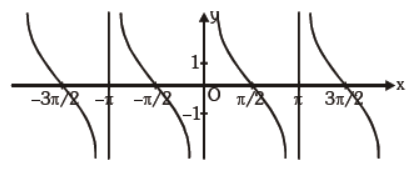
(a) y = − tan x
(b) y = sec x
(c) y = 2 sin x
(d) y = cot x
Answer
D
Question. If x = a cosecnq and y = b cotnq, then by eliminating q
(a) (x/a)2/n + (y/b)2/n = 1
(b) (x/a)2/n − (y/b)2/n = 1
(c) (x/a)2 − (y/b)2 = 1
(d) (x/a)1/n − (y/b)1/n = 1
Answer
B
Question. If x and y are complementary angles, then
(a) sin x = sin y
(b) tan x = tan y
(c) cos x = cos y
(d) sec x = cosec y
Answer
D
Question. If sin A − cos A = 0, then the value of sin4A + cos4A is
(a) 2
(b) 1
(c) 3/4
(d) 1/2
Answer
D
Question. The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sunrays meet the ground at an angle of 60°. find the angle between the sunrays and the ground at the time of long shadow.
(a) 60°
(b) 90°
(c) 45°
(d) 30°
Answer
D
Question. From a point on the horizontal plane, the elevation of the top of a hill is 45°. After walking 500 m towards its summit up a slope inclined at an angle of 15° to the horizon the elevation is 75°, the height of the hill is :-
(a) 500√ 6 m
(b) 500√ 3 m
(c) 250√ 6 m
(d) 250√ 3 m
Answer
C
Question. If x = a cos θ and y = b sin θ, then b2x2 + a2y2 =
(a) ab
(b) b2+a2
(c) a2b2
(d) a4b4
Answer
C
Question. Given that sin A = √3/ 2 and cos B = √3/2 , then tan (A + B) =
(a) 1/√3
(b) 1
(c) √3
(d) Not defined
Answer
D
Question. An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. If after10 s the elevation be 30°, the uniform speed of the aeroplane is
(a) 240√3km/hrs
(b) 240/√3km/hrs
(c) 120/√3km/hrs
(d) 120/√3km/hrs
Answer
A
Question. A balloon leaves the earth at point A and rises at a uniform velocity. At the end of 1 1 2 min, an observer situated at a distance of 200 m from A finds the angular elevation of the balloon to be 60°. The speed of the balloon is
(a) 5.87 m/s
(b) 4.87 m/s
(c) 3.87 m/s
(d) 6.87 m/s
Answer
C
Question. If sin2(2/1 ,3/2 , 4/3 ….x – 1/x – 2) = 1 , 0 < x <100 , find the value of x .
(a) 91°
(b) 80°
(c) 49°
(d) 46°
Answer
D
Question. Find the value of the expression [cos (75 + θ) – sec(15 – θ ) – tan(55 + θ) cot(35 – θ )]
(a) – 1
(b) 0
(c) 1
(d) 3/2
Answer
B
Question. If tan26° + tan19°/ x(1- tan 26° tan19°) = cos 60° , what is the value of x ?
(a) 1
(b) √2
(c) 2
(d) √3
Answer
C
Question. If cos3x = cos 30° sin 60° – sin 30° cos 60° , find the value of x.
(a) 60°
(b) 45°
(c) 20°
(d) 30°
Answer
C
Question. What is the numerical value of the expression sin9°/sin48° – cos81°/cos42° .
(a) 1
(b) 1/2
(c) 0
(d) -1
Answer
C
Question. Find the value of √1 – cosA/1 + cosA .
(a) sec A – cot A
(b) cosec A – cot A
(c) 0
(d) 1
Answer
C
Question. In ΔABC , if ∠B = 90°,AB = 5 cm and AC =10 cm, find ∠A and ∠C .

(a) 90°, 45°
(b) 60°°, 30°
(c) 45°, 0°
(d) 90°, 60°
Answer
B
Question. How is cotθ expressed in terms of sinθ ?
(a) 1/√1 – sin2 θ
(b) √1 – sin2 θ/sin θ
(c) 1/sin θ
(d) sin θ/√1 – sin2 θ
Answer
B
Question. Graphs of y = sin x and y = cos x , where 0 ≤ θ ≤ π/2 intersect at a point. Find abscissa.
(a) π/6
(b) π/4
(c) π/3
(d) 0
Answer
B
Question. Given that sin α = 1/2 and cos β = 1/2 , , find the value of (α +β) .
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Answer
D
Question. A boy standing on the ground and flying a kite with 75 m of string at an elevation of 45°. Another boy is standing on the roof of 25 m high building and is flying his kite at an elevation of 30°. Both the boys are on the opposite side of the two kites. Find the length of the string that the second boy must have, so that the kites meet.
(a) 43.05 m
(b) 34.05 m
(c) 45.05 m
(d) 56.05 m
Answer
D
Question. The angle of elevation of a cloud from a point x m above a take is q and the angle of depression of its reflection in the take is 45°. The height of the cloud is
(a) x tan (45° −θ)
(b) x tan (45° + θ)
(c) 1/ x cot (45° − θ)
(d) 1/ x cot (45° + θ)
Answer
B
Question. Two poles of height a and b stand at the centres of two circular plots which touch each other externally at a point and the two poles subtend angles of 30° and 60° respectively at this point, then distance between the centres of these plots is :-
(a) a + b
(b) (3a +b)/√3
(c) a+3b/√3
(d) a√3 + b
Answer
B
Question. If sinA/ sinB = p and cosA/ cosB = q, then tan B is equal to
(a) ± p/q√q2 −1/1 −p2
(b) ± √q2 −1/1 −p2
(c) ± p/q√p2 −1/1 −q2
(d) None of these
Answer
B
Question. If Tn = sinn θ + cosn θ, then 2T6 − 3T4 + 1 is equal to
(a) 0
(b) sin θ
(c) cos θ
(d) 2 sin θ cos θ
Answer
A
Question. From the top of a light house, the angles of depression of two stations on opposite sides of it at distance ‘a’ apart are a and b. The height of the light house is
(a) a/ cotα cotβ
(b) a/ cotα + cotβ
(c) a cotα cotβ/ cotα + cotβ
(d) a tanα cotβ/ cotα +cotβ
Answer
B
Question. If Tn = sinn θ + cosn θ, then 6T10 − 15T8 + 10T6 − 1 is equal to
(a) 0
(b) 1
(c) sin2 θ
(d) sin3 θ
Answer
A
Question. If the angle of elevation of an object from a point 100 m above a lake is found to be 30° and the angle of depression of its image in lake is 45°, then the height of the object above the lake is
(a) 100(2−√3)m
(b) 100(2+√3)m
(c) 100(√3 −1)m
(d) 1000(√3 +1)m
Answer
B
Question. If sin q and cos θ are the roots of ax2 + bx + c = 0 (ac ≠ 0), then
(a) a2 + b2 − 2ac = 0
(b) a2 − b2 + 2ac = 0
(c) (a + c)2 = b2 + c2
(d) None of these
Answer
B,C
Question. A flagstaff stands vertically on a pillar, the height of the flagstaff being double the height of the pillar. A man on the ground at a distance finds that both the pillar and the flagstaff subtend equal angles at his eyes. The ratio of the height of the pillar and the distance of the man from the pillar is
(a) 1 : 3
(b) 3:√1
(c) 1:√3
(d) √3 :2
Answer
C
Question. If cosθ − sinθ = √2 sinq, then cos θ + sin θ
(a) √2 sin θ
(b) √2 cos θ
(c) 2 cos θ
(d) 2 sin θ
Answer
B
Question. If x sin3θ + y cos3θ = sinq cos θ and x sin θ − y cos q = 0. Then x2 + y2 =
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
Question. The value of sin2 A +cos2 A/sin2A + cosA +cos3 A −sin3 A/cos A−sin A is
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
C
Question. cotθ −cosec θ+1/ cotθ +cosec θ −1 is equal to
(a) 1
(b) cot θ + cosec θ
(c) cosec θ − cot θ
(d) None of these
Answer
C
Question. The distance between two multistoried buildings is 60 m. The angle of depression of the top of the first building as seen from the top of the second building which is 150 m high is 30°. The heigth of the first building is
(a) (150 + 20√3)m
(b) (150 −20√3)m
(c) (150 +10√3)m
(d) (15 −10√3)m
Answer
B
Question. A flagstaff 5 m high stands on a building 25 m high. At an observer at a height of 30 m, the flagstaff and the building subted equal angles. The distance of the observe from the top of the flagstaff is :-
(a) 5 √3/ 2
(b) 5√3/2
(c) 5√2/ 3
(d) None
Answer
B
Question. The value of 5 tan2 A − 5 sec2 A + 1 is equal to
(a) 6
(b) −5
(c) 1
(d) − 4
Answer
D
Question. The perimeter of a triangle ABC is 6 times the A.M. of the sines of its angles. If a = 1, the angle A (acute) is
(a) π/2
(b) π/3
(c) π/4
(d) π/6
Answer
D
Question. Man on a cliff observes a boat at an angle of de- pression of 30° which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of de- pression of the boat is found to be 60°. Find the time taken by the boat to reach the shore.
(a) 6 min.
(b) 7 min.
(c) 8 min.
(d) 9 min.
Answer
D
Question. In an equilateral triangle the inradius r and circumradius R are connected by
(a) r = R/ 3
(b) r = R/ 2
(c) r = 4R
(d) None
Answer
B
Question. If cos A = 5 /13 , find the value of tan A + cot A
(a) 169/ 60
(b) 12/13
(c) 1
(d) 60/ 169
Answer
A
Question. If 2 sin 2θ = √3 , then the value of θ is:
(a) 90º
(b) 30º
(c) 60º
(d) 45º
Answer
B
Question. If 5x = sec θ and 5/ x = tan θ then find the value of 5(x2 -1/x)2
(a) 5
(b) 1/ 5
(c) 2/ 5
(d) 0
Answer
B
Question. If sin A + sin2 θ = 1, then the value of the expression (cos2 A + cos4 A) is:
(a) 1
(b) 1/ 2
(c) 2
(d) 3
Answer
A
Question. Given that sin α = √3/2 and cos β = 0, then the value of β – α is:
(a) 0°
(b) 90°
(c) 60°
(d) 30°
Answer
B
Question. If sin (A + B) = cos (A – B) = 1, then
(a) A = B = 0
(b) A = B = 45°
(c) A = 60°, B = 30°
(d) None of these
Answer
B
Question. The value of (1 + cos θ) (1 − cos θ) cosec2 θ =
(a) 0
(b) 1
(c) cos2 θ
(d) sin2 θ
Answer
B
Question. If θ = 45° then sec θ cot θ – cosec θ tan θ is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. If tan A = 4/3 , the value of sin A is
(a) 4/ 5
(b) 3 /4
(c) 5 /3
(d) 7/ 5
Answer
D
Question. 4 tan2 A – 4 sec2 A is equal to:
(a) 2
(b) 3
(c) 4
(d) –4
Answer
D
Question. If 3 cos θ = 1, then cosec θ is equal to:
(a) 2 √2
(b) 3/ 2√2
(c) 2√3/3
(d) 4/3√2
Answer
B
Question. If sin θ – cos θ = 0, then the value of (sin4 θ + cos4 θ) is:
(a) 1
(b) 3/ 4
(c) 1/ 2
(d) 1/ 4
Answer
C
Question. If x = a sin θ and y = a cos θ, then the value of x2 + y2 is
(a) a
(b) a2
(c) 1
(d) b2
Answer
B
Question. If 3 tan A = 4, then the value of 3 sin A + 2sec A/3 sin A – 2cos A is:
(a) 4
(b) 11/ 15
(c) 7 /15
(d) 3
Answer
D
Question. If cosec θ – cot θ = 1/ 3 , then the value of cosec θ + cot θ is:
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. If the height and length of the shadow of a man are the same, then the angle of elevation of the sun is:
(a) 45º
(b) 60º
(c) 90º
(d) 120º
Answer
A
Question. If sin θ + cos θ = cos θ, (θ ≠ 90°) then the value of tan θ is:
(a) √2 − 1
(b) √2 + 1
(c) √2
(d) – √2
Answer
A
True Or False :
Question. cos θ = a2 +b2/2ab, where a and b are two distinct numbers such that ab > 0.
Answer
False
Question . If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
Answer
False
Question. If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
Answer
True
Question. The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
Answer
False
Fill in the Blanks :
Question. If tan A = 1, then 2 sin A cos A = ………………..
Answer
1
Question. If tan θ + cot θ = 2, then the value of tan2 θ + cot2 θ is ……………….. .
Answer
tan2 θ + cot2 θ = (tan θ + cot θ)2 – 2 tan θ cot θ = (2)2 – 2 × 1 = 2
Question. If sin θ – cos θ = 0, 0 ≤ θ ≤ 90° then the value of q is ……………….. .
Answer
45º
Question. Simplest form of 1+tan2 A/1+cot2 A is
Answer
(tan2A)
Question. If tan θ = √3 , then sec θ = ………………. .
Answer
tan θ = √3 gives θ = 60°
Question. The value of (sin2θ +1/1+tan2θ )………………..
Answer
A
Question. Simplest form of (1 − cos2A) (1 − cot2A) is ……………….. .
Answer
1
Question. cos 1º cos 2º cos 3º …. cos 180º = ……………….. .
Answer
0
Question. In the figure, the angles of depressions from the observing postitions O1 and O2,respectively of the object A are ……………….., ……………….. .
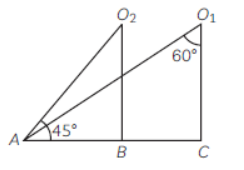
Answer
(30º, 45º)
Question. Maximum value of 1/cosec i is ……………….. .
Answer
1 cosec θ = 1/1 = sin θ
Question. If 3 sec θ – 5 = 0 then cot θ = ……………….. .
Answer
3/ 4
In ΔABC, right angled at B
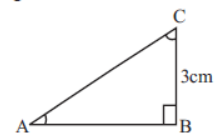
AB + AC = 9 cm and BC = 3cm.
Question. The value of sec C is
(a) 4/ 3
(b) 5/ 3
(c) 1/ 3
(d) None of these
Answer
B
Question. The value of cot C is
(a) 3/ 4
(b) 1/ 4
(c) 5/ 4
(d) None of these
Answer
A
Question. sin2C + cos2C =
(a) 0
(b) 1
(c) –1
(d) None of these
Answer
B
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
Question. Assertion: In a right angled triangle, if tan θ = 3/ 4 , the greatest side of the triangle is 5 units.
Reason: (greatest side)2 = (hypotenuse)2 = (perpendicular)2 + (base)2.
Answer
A
Question. Assertion : In a right angled triangle, if cos θ = 1/ 2 and sin θ = √3/ 2 , then tan θ = √3
Reason: tan θ = sinθ/ cos θ
Answer
A

We hope you liked the above provided MCQ Questions Chapter 8 Trigonometry Class 10 Mathematics with solutions. If you have any questions please ask us in the comments box below.


