MCQ Questions Chapter 5 Continuity and Differentiability Class 12 Mathematics

Please refer to MCQ Questions Continuity and Differentiability Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Continuity and Differentiability in Class 12 Mathematics provided below to get more marks in exams.

Continuity and Differentiability MCQ Questions

Question. The derivative of cos-1 (2x² – 1) with respect to cos-1 x is
(a) 2
(b) 1- 2x
(c) 2/x
(d) 1 – x²

Question

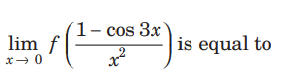
(a) 9/2
(b) 2/ 9
(c) 0
(d) − 9/2 

Question:

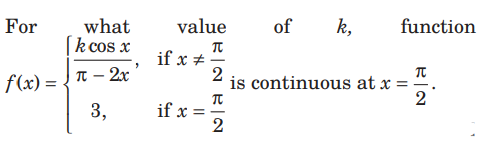
(a) 1
(b) 3
(c) R
(d) 6 

Question:

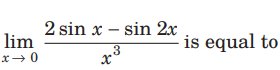
(a) 1
(b) –1
(c) 0
(d) does not exist 

Question:

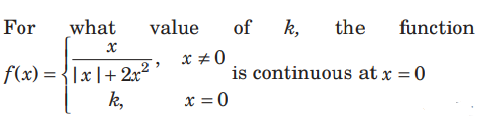
(a) 1 /2
(b) 1
(c) 3/ 2
(d) no value 

Question:

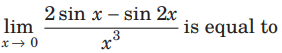
(a) 1
(b) 0
(c) –1
(d) does not exist 

Question:

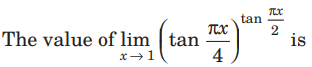
(a) e ⁻²
(b) e ⁻¹
(c) e
(d) 1 

Question:

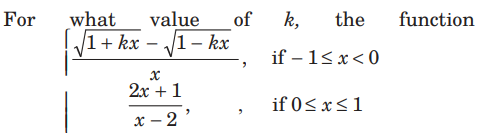
continuous at x =0
(a) 1/ 2
(b) 1
(c) -3/ 2
(d) -1/2 

Question: The value of a and b such that the function f defined

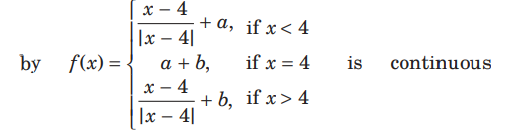
function at x = 4, are
(a) a = 1and b = −1
(b) a = −1and b = 1
(c) a = 0 and b = −1
(d) a = 1and b = 0

Question:

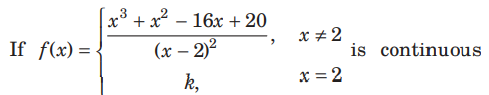
at x = 2, then the value of k is
a) 1
(b) 3
(c) 6
(d) 7 

Question:

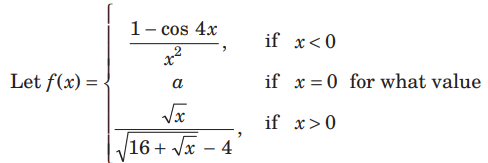
of a, f is continuous at x = 0 ?
(a) 2
(b) 4
(c) 6
(d) 8 

Question: The values of a and b. Such that the function defined

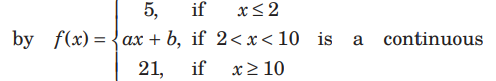
function is
(a) a = 1and b = 2
b) a = 2 and b = 1
(c) a, b ∈ R 
(d) None of these 

Question:

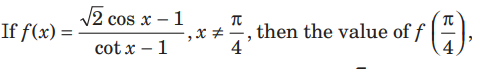
so that f (x ) becomes continuous at x = π/ 4 is
(a) 1/ 2
(b) − 1/ 2
(c) 1
(d) 9  

Question:

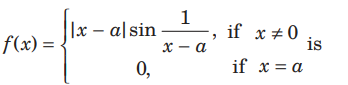
(a) discontinuous at x = 1
(b) discontinuous at x = 2
(c) continuous at x = 1
(d) None of these 

Question:

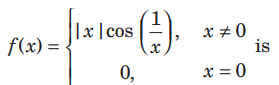
(a) discontinuous at x = 0
(b) continuous at x = 0
(c) does not exist
(d) None of these 

Question: For what value of k,

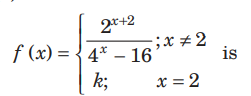
continuous at x = 2
(a) 1
(b) 3 /2
(c) 2
(d) 1/ 2

Question: The number of points at which the function

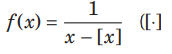
denotes, the greatest integer function) is not continuous is
(a) 1
(b) 2
(c) 3
(d) None of these 

Question: value of a in order that f (x) may be continuous at x = 0 is
(a) − 8
(b) 8
(c) − 4
(d) 4 

Question:

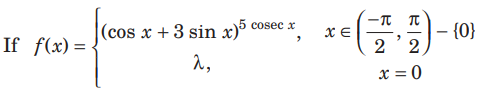
is continuous at x = 0, then λ will be
(a) e ¹⁵
(b) e ²
(c) 15
(d) 1 

Question:

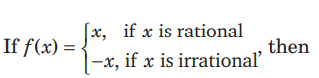
(a) f(x) is an odd function
(b) f (x) is continuous at x = 1 /2
(c) f (x) is continuous at x = 0
(d) f (x) is a periodic function

Question: The function

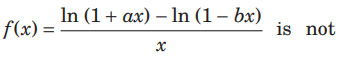
defined at x = 0.The value which should be assigned to f at x = 0, so that it continuous at x = 0, is

(a) a- b 
(b) a+ b 
(c) ln a -ln b
(d) ln a+ ln b 

Question:

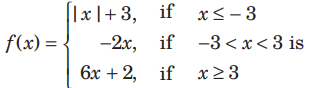
(a) continuous at x = − 3 and discontinuous at x = 3
(b) continuous at x = − 3, 3
(c) discontinuous at x = − 3, 3
(d) continuous at x = 3 and discontinuous at x = 3

Question: The function f(x) = |x|+ |x| /x + is
(a) continuous at the origin
(b) discontinuous at the origin because |x|  is discontinuous there
(c) discontinuous at the origin because |x| /x is discontinuous there
(d) discontinuous at the origin because both | x| and |x|/ x  are discontinuous there 

Question: discontinuity of g(x) = f[f (x)] = is/are
(a) only at x = 1
(b) x = 2, 3
(c) only at x = 3
(d) x = 1, 2 

Question:

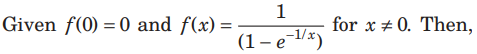
only one of the following statements on f (x ) is true. That is f ( x) is
(a) continuous at x = 0
(b) not continuous at x = 0
(c) both continuous and differentiable at x = 0
(d) not defined at x = 0 

Question:

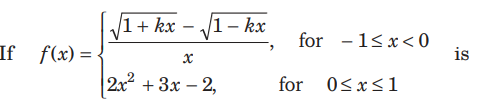
continuous at x = 0, then k is equal to
(a) − 4
(b) − 3
(c) − 2
(d) − 1 

Question: The function f given by

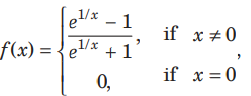
is
(a) discontinuous at x = 0
(b) continuous at x = 0
(c) continuous everywhere
(d) None of the above

Question:

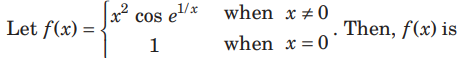
(a) discontinuous at x = 0
(b) continuous but not differentiable at x = 0
(c) differentiable at x = 0
(d) lim (x)  f exist 
     ^{x→ 0}

Question:

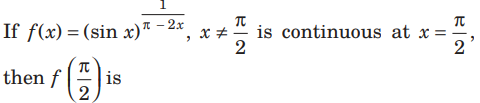
(a) 0
(b) 1
(c) e
(d) None of these 

Question: Let

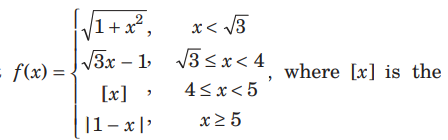
greatest integer ≤ x. The number of points of discontinuity of f (x) is R is
(a) 3
(b) 0
(c) infinite
(d) 1 

Question: If the function

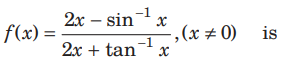
continuous at each point of its domain, then the value of f(0 )is
(a) 2
(b) 1/ 3
(c) 2/ 3
(d) − 1/3 

Question: continuous at x = 0, the value of f (0) should be
(a) −1
(b) 0
(c) −2
(d) 2 

Question:

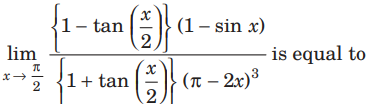
(a) 1/ 8
(b) 0
(c) 1/ 32
(d) ∞

Question

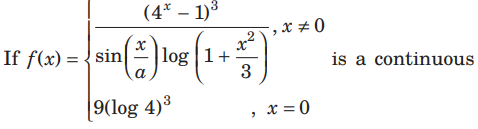
function at x = 0, then the value of a is equal to
(a) 3
(b) 1
(c) 2
(d) 0 

Question:

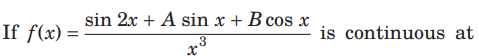
x = 0, then the values of A and B also f( 0) are
(a) A = − 2, B = 0 and f(0)  = − 1
(b) A = 0, B = − 2 and f(0) = 1
(c) A = 1, B = −1 and f(0) 0 =
(d) None of the above

Question: The function

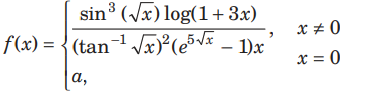
is continuous in [0, 1], if
(a) a = 0
(b) a = 3 /5
(c) a = 2
(d) a = 5/3 

Question. If x = a cos4 θ, y = a sin4 θ ; then dy/dx at θ = 3π/4 is
(a) -1
(b) 1
(c) -a²
(d) a²

Question. If y = log(1−x²/1+x²), then derivative of y with respect to x is
(a) 4x³/(1−𝑥4)
(b) −4x/(1−𝑥4)
(c) 1/ (4−𝑥4)
(d) −4x³/ (1−𝑥4)

Question. If sec (x−y/ x+y) = a, then dy/dx is
(a) –y/x
(b) x/y
(c) –x/y
(d) y/x

Question. The derivative of sin-1 (2x/1+x ²) with respect to cos-1 (1−x²/1+x² ) is
(a) -1
(b) 1
(c) 2
(d) 4

Question. The derivative of f(x) = 3| 2+ x | at x = -3 is
(a) 3
(b) 0
(c) -3
(d) does not exist

Question. If x = t², y = t³, then the value of d² y/ dx² is
(a) 3/2
(b) 3/4t
(c) 3/2t
(d) 34t

Question. Assertion(P) :Sin |x| is differentiable at x= 0
Reason (Q) :Sinx is continuous at x= 0.
Which of the following is true ?
(a) Both P and Q are true and Q is the correct explanation for P.
(b) Both P and Q are true but Q is not correct but Q is false.
(c) P is true but Q is false.
(d) P is false but Q is true

Question. If y = a( 1+ cost) and x = a( t –sint) , then dy/dx is equal to
(a) tan(t/2)
(b) – tan(t/2)
(c) – cot(t/2)
(d) none of these

Question.The set of points where the Function f(x) = |2x-1|cosx is differentiable is
(a) R
(b) R – {1/2}
(c) (0 , ∞)
(d) None of these

Question. If xy = ex-y , then the value of dy/dx is
(a) (1+x)/(1+logx)
(b) (1−logx)/(1+logy)
(c) not defined
(d) logx/(1+logx) ²

Question.The function f(x) = cot x is discontinuous on the set
(a) {x = nπ , n ∈ Z}
(b) {x = 2nπ , n ∈ Z}
(c) {x = (2n + 1) π/2 , n ∈ Z}
(d) {x = nπ/2 , n ∈ Z}

Question. If y = √(sinx + y) , then dy/dx is equal to
(a) cosx/(2y−1)
(b) cosx/(1−2y)
(c) sinx/(1−xy)
(d) sinx/(2y−1)

Question. The function f(x) = [x] , where [x] denotes the greatest integer function , is continuous and differentiable at
(a) -2
(b) 1
(c) 4
(d)1.7

Question. The function f(x) = x | x| ;at x = 0 is
(a) Continuous but not differentiable
(b) Differentiable but not continuous
(c) Continuous and Differentiable
(d) Neither Continuous nor differentiable

Question. Let f(x) = |sin x| Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ , n ∈ Z
(c) f is everywhere continuous but not differentiable at x = (2n + 1) π/2 , n ∈ Z
(d) None of these

Question.The function f(x) = e|x| is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) None of these

Question. If y = (tan x)sin x, then dy/dx is equal to
(a) sec x + cos x
(b) sec x+ log tan x
(c) (tan x)sin x
(d) None of these

Question. If xx = yy, then dy/dx is equal to
(a) –y/x
(b) –x/y
(c) 1 + log (x/y )
(d) ( 1+logx)/(1+logy)

Question. If x = sin-1 (3t – 4t³) and y = cos-1 √(1-t ²) then dy/dx is equal to
(a) ½
(b) 2/5
(c) 3/2
(d) 1/3

Question. If (image 33) is continuous at x = 0, then a + 2b is equal to:
(a) 1
(b) –1
(c) 0
(d) –2

Question. Let f and g be differentiable functions on R such that fog is the identity function. If for some a, b ∈ R, g'(a) = 5 and g(a) = b, then f'(b) is equal to:
(a) 1/5
(b) 1
(c) 5
(d) 2/5

Question. Consider the function, f(x) = | x – 2 | ‘+ | x – 5 |, x ∈ R.
Statement-1 : f'(4) = 0
Statement-2 : f is continuous in [2,5], differentiable in (2,5) and f(2) = f(5).
(a) Statement-1 is false, Statement-2 is true.
(b) Statement-1 is true, statement-2 is true; statement-2 is a correct explanation for Statement-1.
(c) Statement-1 is true, statement-2 is true; statement-2 is not a correct explanation for Statement-1.
(d) Statement-1 is true, statement-2 is false.

Question. If f(x) = a |sinx| + be^|x| + c|x|³, where a, b, c ∈ R, is differentiable at x = 0, then
(a) a = 0, b and c are any real numbers
(b) c = 0, a = 0, b is any real number
(c) b = 0, c = 0, a is any real number
(d) a = 0, b = 0, c is any real number

Question. If the function f defined on (π/6, π/3) by (image 5) is continuous, then k is equal to:
(a) 2
(b) 1/2
(c) 1
(d) 1/√2

Question. Let f : [– 1, 3] → R be defined as (image 8) where [t] denotes the greatest integer less than or equal to t. Then, f is discontinuous at :
(a) only one point
(b) only two points
(c) only three points
(d) four or more points

Question. Let (image 11) The value of k for which f is continuous at x = 2 is
(a) e^–2
(b) e
(c) e^–1
(d) 1

Question. The value of k for which the function (image 12) is continuous at x = π/2, is :
(a) 17/20
(b) 2/5
(c) 3/5
(d) – 2/5

Question. If xlog_e(log_ex) – x² + y² = 4(y > 0), then dy/dx at x = e is equal to:
(image 45)

Question. Let K be the set of all real values of x where the function f(x) = sin | x | – | x | + 2 (x – π) cos | x | is not differentiable. Then the set K is equal to :
(a) Φ (an empty set)
(b) {p}
(c) {0}
(d) {0, π}

Question. If the function (image 15) is continuous at x = π, then k equals:
(a) 0
(b) 1/2
(c) 2
(d) 1/4

Question. If (image 78) then dy/dx is equal to.
(a) y/x
(b) – y/x
(c) – x/y
(d) x/y

Question. If (image 79)
(a) Exists and is equal to – 2
(b) Does not exist
(c) Exist and is equal to 0
(d) Exists and is equal to 2

Question. Let f be a composite function of x defined by
(image 18)
Then the number of points x where f is discontinuous is :
(a) 4
(b) 3
(c) 2
(d) 1

Question. Let f (x) = x.[x/2], for –10 < x < 10, where [t] denotes the greatest integer function. Then the number of points of discontinuity of f is equal to ______.

Question. If a function f (x) defined by (image 2) be continuous for some a, b, c ∈ R and f ‘(0) + f ‘(2) = e, then the value of a is :
(a) 1/(e² – 3e -13)
(b) e/(e² – 3e +13)
(c) e/(e² + 3e +13)
(d) e/(e² – 3e +13)

Question. Let f(x) = – 1 + | x – 2 |, and g(x) = 1 – | x |; then the set of all points where fog is discontinuous is :
(a) {0, 2}
(b) {0, 1, 2}
(c) {0}
(d) an empty set

Question. If f : R → R is a function defined by f(x) = [x] cos ((2x – 1) / 2)π, where [x] denotes the greatest integer function, then f is .
(a) continuous for every real x.
(b) discontinuous only at x = 0
(c) discontinuous only at non- ero integral values of x.
(d) continuous only at x = 0.

Question. Let S be the set of all points in (–π,π) at which the function f(x) = min {sinx, cosx} is not differentiable. Then S is a subset of which of the following?
(image 74)

Question. For x > 1, if (2x)^2y = 4e^2x-2y, then (1 + log_e2x)²dy/dx is equal to :
(image 75)

Question. Define f(x) as the product of two real functions
(image 23)
Statement – 1 : f(x) is continuous on R.
Statement – 2 : f₁(x) and f₂(x) are continuous on R.
(a) Statement -1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(b) Statement-1 is true, Statement-2 is true; Statement-2 is NOT a correct explanation for Statement-1
(c) Statement-1 is true, Statement-2 is false
(d) Statement-1 is false, Statement-2 is true

Question. The values of p and q for which the function
(image 24)
(a) p = 5/2, q = 1/2
(b) p = − 3/2, q = 1/2
(c) p = 1/2, q = 3/2
(d) p = 1/2, q = − 3/2

Question. If f(x) = sin (sin x) and f”(x) + tan x f'(x) + g(x) = 0, then g(x) is :
(a) cos² x cos (sin x)
(b) sin² x cos (cos x)
(c) sin² x sin (cos x)
(d) cos² x sin (sin x)

Question. Consider a quadratic equation ax² + bx + c = 0, where 2a + 3b + 6c = 0 and let g(x) = a(x³/3) + b(x²/2) + cx.
Statement 1: The quadratic equation has at least one root in the interval (0, 1).
Statement 2: The Rolle’s theorem is applicable to function g(x) on the interval [0, 1].
(a) Statement 1 is false, Statement 2 is true.
(b) Statement 1 is true, Statement 2 is false.
(c) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation for Statement 1.
(d) Statement 1 is true, Statement 2 is true, , Statement 2 is a correct explanation for Statement 1.

Question. The function f : R /{0} → R given by f(x) = 1/x − 2/(e^2x − 1) can be made continuous at x = 0 by defining f (0) as
(a) 0
(b) 1
(c) 2
(d) – 1

Question. Let S = { |x| t ∈ R : f (x) =| x – π | (e^|x|-1)sin | x | is not differentiable at t}. Then the set S is equal to :
(a) {0}
(b) {π}
(c) {0, π}
(d) Φ(an empty set)

Question. Let S = {(λ, m) ∈ R × R : ƒ(t) = (|λ|e^|t| – μ). sin (2|t|), t ∈ R, is a differentiable function}. Then S is a subest of?
(a) R × [0, ∞)
(b) (–∞, 0) × R
(c) [0, ∞) × R
(d) R × (–∞, 0)

Question. Let f : R → R be a function defined by f(x) = max{x, x²}. Let S denote the set of all points in R, where f is not differentiable. Then
(a) {0, 1}
(b) {0}
(c) Φ (an empty set)
(d) {1}

Question. Suppose a differentiable function f(x) satisfies the identity f(x + y) = f(x) + f(y) + xy² + x²y, for all real x and y. If (image 31) then f'(3) is equal to ___________.

Question. If for x ∈ (0, 1/4), the derivative of tan^-1( (6x√x) / (1–9x³) ) is √x.g(x) , then g(x) equals :
(a) 3/(1 + 9x³)
(b) 9/(1 + 9×3)
(c) 3x√x/(1 – 9x³)
(d) 3x/(1 – 9x³)

We hope you liked the above provided MCQ Questions Continuity and Differentiability Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.