Please refer to MCQ Questions Chapter 4 Determinants Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 4 Determinants in Class 12 Mathematics provided below to get more marks in exams.
Chapter 4 Determinants MCQ Questions
Question. If area of triangle is 4 sq units with vertices (–2, 0), (0, 4) and (0, k), then k is equal to
(a) 0, –8
(b) 8
(c) – 8
(d) 0, 8
Answer
D
Question. Find the cofactors of elements a12, a22, a32, respectively of the matrix

(a) 0, 2, – 2 sin θ
(b) 2, 0, 2sin θ
(c) 2, 0, –2 sin θ
(d) – 2sin θ, 2, 0
Answer
A
Question.
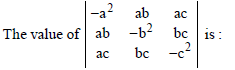
(a) 0
(b) abc
(c) 4a2b2c2
(d) None of these
Answer
C
Question. For any 2 × 2 matrix A, if
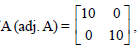
then | A | is equal to :
(a) 0
(b) 10
(c) 20
(d) 100
Answer
B
Question. Value of the determinant (when n ∈ N)
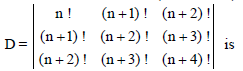
(a) (n!)2 (2n3 –8n2 )
(b) (2n!)3 (3n2 + 4n –5)
(c) (n!)3 (2n3 +8n2 +10n + 4)
(d) None of these
Answer
C
Question. The number of values of k for which the system of equations (k+1)x+8y = 4k; kx + (k + 3) y = 3k – 1 has infinitely many solutions is
(a) 0
(b) 1
(c) 2
(d) infinite
Answer
B
Question. The area of the triangle formed by the points (1, 2), (k, 5) and (7, 11) is zero then the value of k is
(a) 0
(b) 3
(c) 5
(d) 7
Answer
B
Question. If rows and columns of the determinant are interchanged, then its value
(a) remains unchanged
(b) becomes change
(c) is doubled
(d) is zero
Answer
A
Question. Suppose α,β,γ∈ R are such that sin α, sinβ, sin γ ≠ 0 and
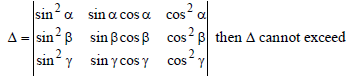
(a) 1
(b) 0
(c) – 1/2
(d) None of these
Answer
A
Question.
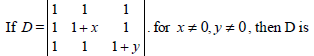
(a) divisible by x but not y
(b) divisible by y but not x
(c) divisible by neither x nor y
(d) divisible by both x and y
Answer
D
Question.

Answer
D
Question.
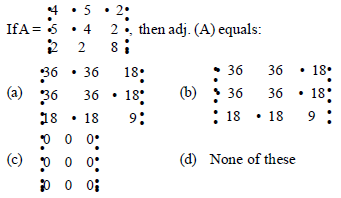
Answer
B
Question.

(a) 52
(b) 1
(c) 1/5
(d) 5
Answer
C
Question. The roots of the equation
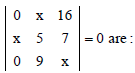
(a) 0, 12 and 12
(b) 0 and ±12
(c) 0, 12 and 16
(d) 0, 9 and 16
Answer
B
Question. If x is positive integer, then
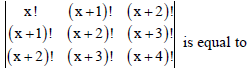
(a) 2x! (x + 1)!
(b) 2x! (x + 1)! (x + 2)!
(c) 2x! (x + 3)!
(d) 2(x + 1)! (x + 2)! (x + 3)!
Answer
B
Question. If a2 + b2 + c2 = – 2 and
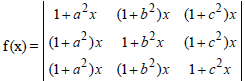
then f (x) is a polynomial of degree
(a) 1
(b) 0
(c) 3
(d) 2
Answer
D
Question.
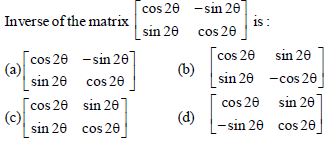
Answer
D
Question.
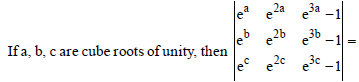
(a) 0
(b) e
(c) e2
(d) e3
Answer
A
Question.

If B is the inverse of matrix A, then α is
(a) 5
(b) –1
(c) 2
(d) –2
Answer
A
Question.

Answer
C
Question.
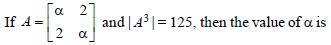
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 5
Answer
C
Question.
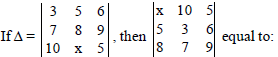
(a) Δ
(b) –Δ
(c) Δx
(d) 0
Answer
B
Question.

(a) k2Δ
(b) k3Δ
(c) kΔ
(d) k4Δ
Answer
B
Question. If each of third order determinant of value Δ is multiplied by 4, then value of the new determinant is:
(a) Δ
(b) 21Δ
(c) 64Δ
(d) 128Δ
Answer
C
Question. If cij is the cofactor of the element aij of the determinant
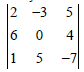
then write the value of a32.c32
(a) 110
(b) 22
(c) – 110
(d) – 22
Answer
A
Question. The parameter on which the value of the determinant
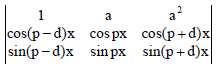
does not depend upon is
(a) a
(b) p
(c) d
(d) x
Answer
B
Question. If A and B are square matrices and A –1 and B–1 of the same order exist, then (AB)–1 is equal to :
(a) AB–1
(b) A–1 B
(c) A–1 B–1
(d) B–1 A–1
Answer
D
Question.

(a) 0
(b) 3
(c) 5
(d) 7
Answer
A
Question. The solution set of the equation

(a) {0, 1}
(b) {1, 2}
(c) {1, 5}
(d) {2, – 1}
Answer
D
Question.
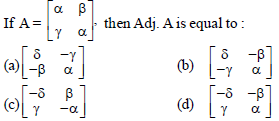
Answer
B
Question. For positive numbers x, y, z, the numerical value of the
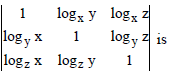
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
A
Question. If A, B, C are the angles of a triangle, then the value of determinant
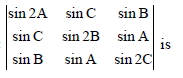
(a) π
(b) 0
(c) 2 π
(d) None of these
Answer
B
Question.
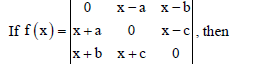
(a) f (a) = 0
(b) f (b) = 0
(c) f (0) = 0
(d) f (1) = 0
Answer
C
Question.
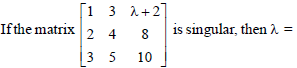
(a) –2
(b) 4
(c) 2
(d) – 4
Answer
B
Question.
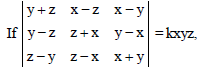
then the value of k is :
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question. If A and B are two matrices such that A + B and AB are both defined, then
(a) A and B are two matrices not necessarily of same order.
(b) A and B are square matrices of same order.
(c) Number of columns of A = Number of rows of B.
(d) None of these.
Answer
B
Question. If the system of linear equations
x + 2ay + az = 0
x + 3by + bz = 0
x + 4cy + cz = 0
has a non – zero solution, then a, b, c
(a) satisfy a + 2b + 3c = 0
(b) are in A.P
(c) are in G..P
(d) are in H.P.
Answer
D
Question.

(a) (a + b)2
(b) (a + b + c + d)2
(c) (a2 + b2 – c2 – d2)
(d) a2 + b2 + c2 + d2
Answer
D
Question. The value of
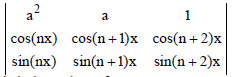
is independent of :
(a) n
(b) a
(c) x
(d) None of these
Answer
A
Question.
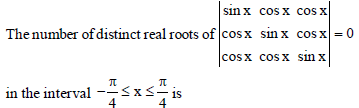
(a) 0
(b) 2
(c) 1
(d) 3
Answer
C
Question. Consider the system of linear equations;
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has
(a) exactly 3 solutions
(b) a unique solution
(c) no solution
(d) infinite number of solutions
Answer
C
Question. If a, b, c are in A. P., then the value of
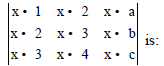
(a) 3
(b) – 3
(c) 0
(d) None of these
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C
(a) 2 1 3
(b) 4 3 1
(c) 4 1 3
(d) 3 1 2
Answer
B
Question.
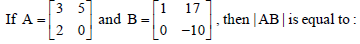
(a) 80
(b) 100
(c) – 110
(d) 92
Answer
B
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Consider the system
2x + 3y + 6z = 8
x + 2y + 3z = 5
x + y + 3z =4
Assertion: The above system of equations has no solution.
Reason: det A = 0 and (adj A)B = 0, where
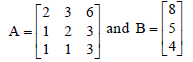
Answer
C
Question. Let A = [aij] be a matrix of order 3 × 3.
Assertion: Expansion of determinant of A along second row and first column gives the same value.
Reason: Expanding a determinant along any row or column gives the same value.
Answer
A
Question.
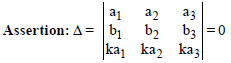
Reason: If corresponding elements of any two rows of a determinant are proportional, then its value is zero.
Answer
A
Question. Assertion: If a, b, c are even natural numbers, then
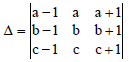
is an even natural number.
Reason: Sum and product of two even natural number is also an even natural number.
Answer
D
Question. Assertion : Δ = a11A11 + a12A12 + a13A13 where, Aij is cofactor of aij.
Reason : Δ = Sum of the products of elements of any row (or column) with their corresponding cofactors.
Answer
A
Question. Assertion : If three lines L1 : a1x + b1y + c1 = 0,
L2 : a2x + b2y + c2 = 0 and
L3 : a3x + b3y + c3 = 0 are concurrent lines, then
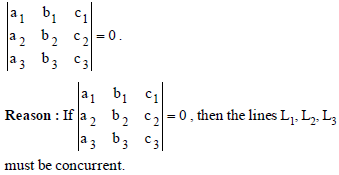
Answer
C
Question. Let (image 6) where b > 0. Then the minimum value of (det (A))/b is:
(a) 2√3
(n) – 2√3
(c) – √3
(d) √3
Answer
A
Question. Let a – 2b + c = 1.
(image 3)
(a) ƒ(–50) = 501
(b) ƒ(–50) = –1
(c) ƒ(50) = –501
(d) ƒ(50) = 1
Answer
D
Question. If (image 12) and A and B are respectively the maximum and the minimum values of f(θ), then (A, B) is equal to:
(a) (3, – 1)
(b) (4, 2 – √2 )
(c) (2 + √2, 2 – √2 )
(d) (2 + √2, -1)
Answer
C
Question. (image 4)
(a) Δ1 – Δ2 = -2x3
(b) Δ1 – Δ2 = x(cos2θ – cos4θ)
(c) Δ1 × Δ2 = – 2(x3 + x -1)
(d) Δ1 + Δ2 = -2x3
Answer
D
Question. The sum of the real roots of the equation
(image 5)
is equal to :
(a) 6
(b) 0
(c) 1
(d) –4
Answer
B
Question. If (image 7) then the ordered pair (A, B) is equal to :
(a) (– 4, 3)
(b) (– 4, 5)
(c) (4, 5)
(d) (– 4, – 5)
Answer
B
Question. (image 8)
(a) 4 + 2√3
(b) -2 + √3
(c) -2 – √3
(d) -4 – 2√3
Answer
C
Question. If (image 9) then the determinant of the matrix (A2016 – 2A2015 – A2014) is :
(a) –175
(b) 2014
(c) 2016
(d) –25
Answer
D
Question. The least value of the product xyz for which the determinant (image 11) is non-negative, is :
(a) -2√2
(b) –1
(c) -16√2
(d) –8
Answer
D
Question. If B is a 3 × 3 matrix such that B2 = 0, then det. [(I + B)50 – 50B] is equal to:
(a) 1
(b) 2
(c) 3
(d) 50
Answer
A
Question. Let (image 1) If B = A + A4, then det (B):
(a) is one
(b) lies in (2, 3)
(c) is zero
(d) lies in (1, 2)
Answer
D
Question. If (image 2) then B + C is equal to :
(a) –1
(b) 1
(c) –3
(d) 9
Answer
C
Question. Let (image 14) Then the number of non-singular matrices in the set S is :
(a) 27
(b) 24
(c) 10
(d) 20
Answer
B
Question. If (image 10) then ‘α’ is equal to :
(a) 24
(b) –12
(c) –24
(d) 12
Answer
A
Question. Statement – 1:
Determinant of a skew-symmetric matrix of order 3 is ero.
Statement – 2 :
For any matrix A, det (A)T= det (A) and det (– A) = – det (A).
Where det (B) denotes the determinant of matrix B. Then :
(a) Both statements are true
(b) Both statements are false
(c) Statement-1 is false and statement-2 is true
(d) Statement-1 is true and statement-2 is false
Answer
D
Question. Let A be a 2 × 2 matrix with real entries. Let I be the 2 × 2 identity matrix. Denote by tr(A), the sum of diagonal entries of a. Assume that A2 = I.
Statement-1 : If A ≠ I and A ≠ –I, then det (A) = –1
Statement-2 : If A ≠ I and A ≠ –I, then tr (A) ≠ 0.
(a) Statement -1 is false, Statement-2 is true
(b) Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
(c) Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
(d) Statement -1 is true, Statement-2 is false
Answer
D
Question. Let A be a 2 × 2 matrix with non- ero entries and let A2 = I , where I is 2 × 2 identity matrix. Define Tr(A) = sum of diagonal elements of A and |A| = determinant of matrix A.
Statement – 1 : Tr(A) = 0.
Statement – 2 : |A| = 1.
(a) Statement-1 is true, Statement-2 is true ; Statement-2 is not a correct explanation for Statement -1.
(b) Statement -1 is true, Statement -2 is false.
(c) Statement -1 is false, Statement -2 is true .
(d) Statement – 1 is true, Statement 2 is true ; Statement -2 is a correct explanation for Statement -1.
Answer
B
Question. Let A, other than I or – I, be a 2 × 2 real matrix such that A2 = I, I being the unit matrix. Let Tr (A) be the sum of diagonal elements of A.
Statement-1: Tr (A) = 0
Statement-2: det (A) = – 1
(a) Statement-1 is true; Statement-2 is false.
(b) Statement-1 is true; Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
(c) Statement-1 is true; Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(d) Statement-1 is false; Statement-2 is true.
Answer
B
Question. Let d ∈ R, and (image 30) q ∈ [0, 2π]. If the minimum value of det (A) is 8, then a value of d is:
(a) – 5
(b) – 7
(c) 2 ( √2 + 1)
(d) 2 ( √2 + 2)
Answer
A
Question. If the minimum and the maximum values of the function (image 21) are m and M respectively, then the ordered pair (m, M) is equal to :
(a) (0, 2√2)
(b) (– 4, 0 )
(c) (– 4, 4)
(d) (0, 4)
Answer
B
Question. Let A = [aij] and B = [bij] be two 3 ´ 3 real matrices such that bij = (3)(i + j – 2) aij, where i, j = 1, 2, 3. If the determinant of B is 81, then the determinant of A is:
(a) 1/3
(b) 3
(c) 1/81
(d) 1/9
Answer
D
Question. If a, b, c, are non-zero complex numbers satisfying a2 + b2 + c2 = 0 and (image 40) then k is equal to
(a) 1
(b) 3
(c) 4
(d) 2
Answer
C
Question. Let α and β be the roots of the equation x2 + x + 1 = 0. Then for y ”’ 0 in R, (image 26) is equal to:
(a) y(y2 – 1)
(b) y(y2 – 3)
(c) y3
(d) y3 – 1
Answer
C
Question. If a1, a2 , a3 , …………, an , …… are in G. P., then the determinant
(image 46)
is equal to
(a) 1
(b) 0
(c) 4
(d) 2
Answer
B
Question. If a + x = b + y = c + z + 1, where a, b, c, x, y, z are non-zero distinct real numbers, then (image 22) is equal to :
(a) y (b – a)
(b) y (a – b)
(c) 0
(d) y (a – c)
Answer
B
Question. The area of the triangle whose vertices are complex numbers z, iz, z + iz in the Argand diagram is
(a) 2|z|2
(b) 1/2|z|2
(c) 4|z|2
(d) |z|2
Answer
B
Question. If a, b, c are sides of a scalene triangle, then the value of (image 39)
(a) non – negative
(b) negative
(c) positive
(d) non-positive
Answer
B
Question. A value of θ ∈ (0, π/3), for which (image 25)
(a) π/9
(b) π/18
(c) 7π/24
(d) 7π/36
Answer
A
Question. The number of distinct real roots of the equaiton, (image 35)
(a) 1
(b) 4
(c) 2
(d) 3
Answer
C
Question. If a2 + b2 + c2 = – 2 and (image 47) then f (x) is a polynomial of degree
(a) 1
(b) 0
(c) 3
(d) 2
Answer
D
Question. Let the numbers 2, b, c be in an A.P. and (image 27) If det(A)?[2, 16], then c lies in the interval :
(a) [2, 3)
(b) (2 + 23/4, 4)
(c) [4, 6]
(d) [3, 2 + 23/4]
Answer
C
Question. If (image 28) det (A) lies in the interval :
(a) (1, 5/2)
(b) [5/2, 4)
(c) (0, 3/2]
(d) (3/2, 3]
Answer
B
Question. If (image 29) = (a + b + c) (x + a + b + c)2, x ≠ 0 and a + b + c ≠ 0, then x is equal to :
(a) abc
(b) – (a + b +c)
(c) 2 (a + b +c)
(d) – 2 (a + b +c)
Answer
B
Question. If a1, a2, a3,……, an ,…. are in G.P., then the value of the determinant (image 48)
(a) –2
(b) 1
(c) 2
(d) 0
Answer
D
Question. Let a1, a2, a3, …, a10 be in G.P. with ai > 0 for i = 1, 2, …, 10 and S be the set of pairs (r, k), r, k ∈ N (the set of natural numbers) for which
(image 31)
Then the number of elements in S, is :
(a) 4
(b) infinitely many
(c) 2
(d) 10
Answer
B
Question. If (image 32) then A is:
(a) invertible for all t ∈ R.
(b) invertible only if t = π.
(c) not invertible for any t ∈ R.
(d) invertible only if t = π/2
Answer
A
Question. Let two points be A(l, – 1) and B(0, 2). If a point P(x’, y’) be such that the area of ΔPAB = 5 sq. units and it lies on the line, 3x + y – 4λ = 0, then a value of λ is:
(a) 4
(b) 3
(c) 1
(d) –3
Answer
B
Question. (image 19)
(a) 1/5
(b) 5
(c) 52
(d) 1
Answer
A
Question. Let k be an integer such that triangle with vertices (k, –3k), (5, k) and (–k, 2) has area 28 sq. units. Then the orthocentre of this triangle is at the point :
(a) (2, 1/2)
(b) (2, − 1/2)
(c) (1, 3/4)
(d) (1, − 3/4)
Answer
A
Question. If the system of linear equations,
x + y + z = 6
x + 2y + 3z = 10
3x + 2y + λz = μ
has more than two solutions, then μ – λ2 is equal to _________.
Answer
13


