Please refer to MCQ Questions Chapter 3 Matrices Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 3 Matrices in Class 12 Mathematics provided below to get more marks in exams.
Chapter 3 Matrices MCQ Questions
Question. If A= [aij] mxn and B= [bij]pxq and AB= BA then
(a) n=p
(b) n=p, m=n
(c) m=n=p=q
(d) m=q
Answer
C
Question: If A and B are matrices of same order, then (AB’- BA’) is a
(a) skew-symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Answer
A
Question: If a, b and c are all different from zero such that 1/a +1/b +1/c=0, then the matrix
(a) symmetric
(b) non-singular
(c) can be written as sum of a symmetric and a skew-symmetric matrix
(d) All of the above
Answer
D
Question: For what value of x, the matrix
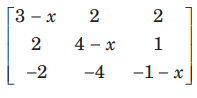
is singular
(a) x = 1, 2
(b) x = 0, 2
(c) x = 0, 1
(d) x = 0 ,3
Answer
D
Question:
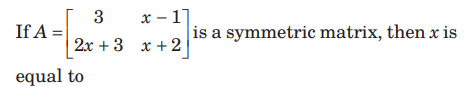
(a) 4
(b) 3
(c) -4
(d) -3
Answer
C
Question: For any 2x 2 matrix A, if A (a d j A) =
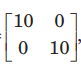
then |A | is equal to
(a) 0
(b) 10
(c) 20
(d) 100
Answer
B
Question: The matrix A =
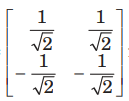
is
(a) unitary
(b) orthogonal
(c) nilpotent
(d) involutory
Answer
C
Question:

Answer
A
Question: If A is a singular matrix, then A adj (A )
(a) is a scalar matrix
(b) is a zero matrix
(c) is an identity matrix
(d) is an orthogonal matrix
Answer
B
Question:
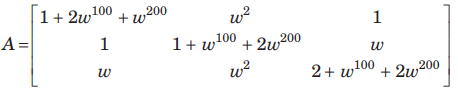
(a) A is singular
(b) | | A ¹ 0
(c) A is symmetric
(d) None of these
Answer
A
Question:
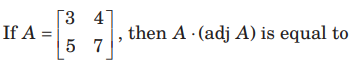
(a) A
(b)| A|
(c) |A | I
d) None of these
Answer
C
Question: Matrix A =
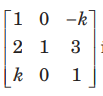
is invertible for
(a) k = 1
(b) k = – 1
(c) k = ± 1
(d) None of these
Answer
C
Question:
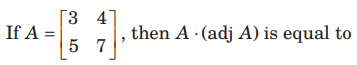
(a) A
(b) |A|
(c) |A|I
(d) None of these
Answer
A
Question: If A is a skew-symmetric matrix of odd order, then A| is equal to
(a) 0
(b) n
(c) n2
(d) None of these
Answer
A
Question:
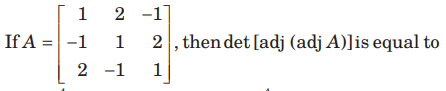
(a) 124
(b) 134
(c) 144
(d) None of these
Answer
C
Question:

Answer
C
Question:
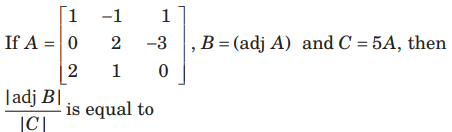
(a) 5
(b) 25
(c) –1
(d) 1
Answer
D
Question:
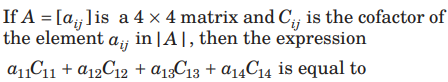
(a) 0
(b) – 1
(c) 1
(d) |A|
Answer
D
Question: If A2– A+I = 0, then the inverse of A is
a) A- I
(b) I- A
(c) A + 1
(d) A
Answer
B
Question:
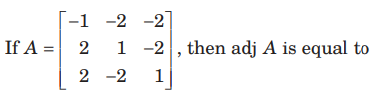
(a) A
(b) A’
(c) 3A
(d) 3A
Answer
D
Question:
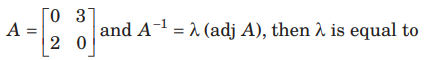
(a) – 1 6
(b) 1/ 3
(c) – 1/ 3
(d) 1/ 6
Answer
A
Question. If A is of order 2x3 and B is of order 3x2, then the order of AB is :
(a) 3x3
(b) 2x2
(c) 3x2
(d) 2x3
Answer
B
Question.
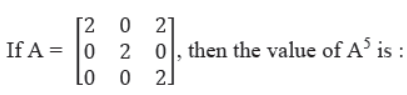
(a) 5A
(b) 10A
(c) 16 A
(d) 32 A
Answer
C
Question.

Answer
B
Question.
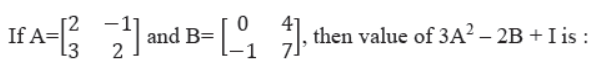
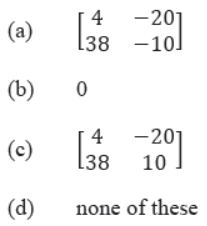
Answer
A
Question.

(a) (3,7)
(b) (9,14)
(c) (5,14)
(d) (3,14)
Answer
B
Question.
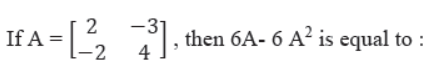
(a) I
(b) 2I
(c) 3I
(d) 4A
Answer
B
Question. If A is a square matrix , then AAT + ATA is :
(a) Unit matrix
(b) null matrix
(c) symmetric matrix
(d) skew-symmetric matrix
Answer
C
Question. If aij= i + j then A = [𝑎𝑖𝑗]3×4 is :
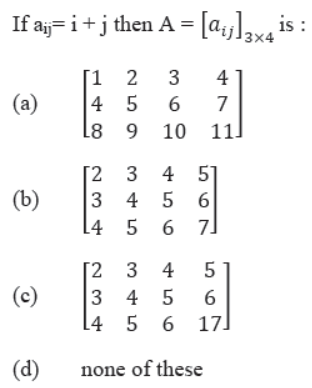
Answer
B
Question.

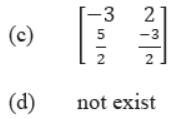
Answer
C
Question.
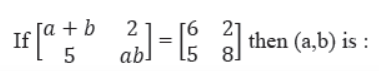
(a) (2,4), (4,2)
(b) (3,3),(3,4)
(c) (2,2),(1,1)
(d) none of above
Answer
A
Question.

(a) 1
(b) 2
(c) 1/2
(d) -2
Answer
C
Question.

Answer
C
Question.

(a) -5
(b) -1/5
(c) 1/25
(d) 25
Answer
B
Question.
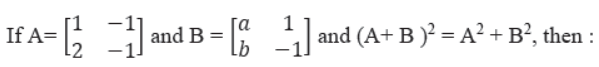
(a) a = 2, b = -3
(b) a = -2, b = -3
(c) a = 1, b = 4
(d) none of above
Answer
C
Question.
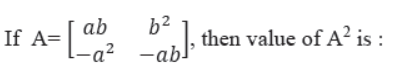
(a) 0
(b) I2
(c) -I2
(d) none of these
Answer
A
Question.

Answer
C
Question.

(d) none of above
Answer
C
Question.
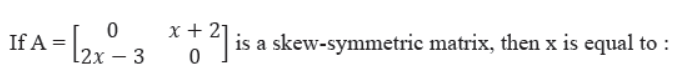
(a) 1/3
(b) 5
(c) 3
(d) 1
Answer
A
Question.

Answer
B
Question.
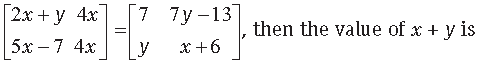
(a) x = 3,y =1
(b) x = 2,y = 3
(c) x = 2,y = 4
(d) x = 3,y = 3
Answer
B
Question. Total number of possible matrices of order 3 x 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512
Answer
A
Question. If A and B are two matrices of the order 3 x m and 3 x n, respectively and m = n, then order of matrix (5A – 2B) is
(a)m x 3
(b) 3 x 3
(c)m x n
(d) 3 x n
Answer
D
Question.
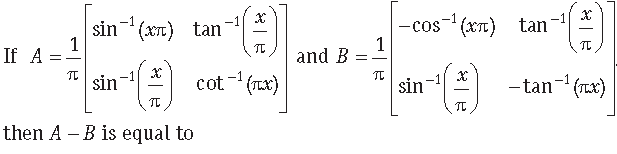
(a) I
(b) 0
(c) 2I
(d) (1/2)I
Answer
D
Question.
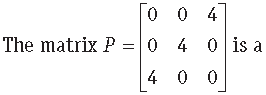
(a) square matrix
(b) diagonal matrix
(c) unit matrix
(d) None of these
Answer
A
Question.
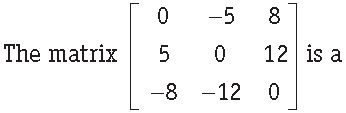
(a) diagonal matrix
(b) symmetric matrix
(c) skew-symmetric matrix
(d) scalar matrix
Answer
C
Question. On using elementary row operation R1 → R1 – 3R2 in the following
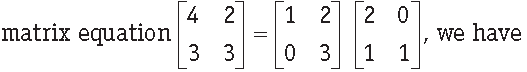

Answer
A
Question. If A is a square matrix such that A2 = I, then (A – I)3 + (A + I)3 – 7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3A
Answer
A
Question. If A is matrix of order m x n and B is a matrix such that AB’ and B’A are both defined, then order of matrix B is
(a) m x m
(b) n x n
(c) n x m
(d) m x n
Answer
D
Question. If matrix A =[ aij ]2×2, where aij = 1, if i ≠ j = 0 and if i = j, then A2 is equal to
(a) I
(b) A
(c) 0
(d) None of these
Answer
A
Question.

(a) identity matrix
(b) symmetric matrix
(c) skew-symmetric matrix
(d) None of these
Answer
B
Question. If A and B are matrices of same order, then (AB’ – BA’) is a
(a) skew-symmetric matrix
(b) null matrix
(c)symmetric matrix
(d) unit matrix
Answer
A
Question. On using elementary column operations C2 → C2 – 2C1 in the
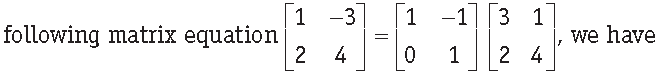

Answer
D
Question. For any two matrices A and B, we have
(a) AB = BA
(b) AB ≠ BA
(c) AB = O
(d) None of these
Answer
D
True/False
Question. Two matrices are equal, if they have same number of rows and same number of columns.
Answer
False
Question. Matrices of different order cannot be subtracted.
Answer
True
Question. A matrix denotes a number.
Answer
False
Question. Matrices of any order can be added.
Answer
False
Question. If matrix AB = 0, then A = 0 or B = 0 or both A and B are null matrices.
Answer
False
Question. Matrix multiplication is commutative.
Answer
False
Question. A square matrix where every element is unity is called an identity matrix.
Answer
False
Question. Matrix addition is associative as well as commutative.
Answer
True
Question. If A and B are two matrices of the same order, then A – B = B – A.
Answer
False
Question. If A and B are two square matrices of the same order, then A + B = B + A.
Answer
True
Question. If A, B and C are square matrices of same order, then AB = AC always implies that B = C.
Answer
False
Question. If each of the three matrices of the same order are symmetric, then their sum is a symmetric matrix.
Answer
True
Question. If A and B are any two matrices of the same order, then (AB)’ = A’B’.
Answer
False
Question. If A is skew-symmetric matrix, then A2 is a symmetric matrix.
Answer
True
Question. Transpose of a column matrix is a column matrix.
Answer
False
Question. If A and B are two square matrices of the same order, then AB = BA.
Answer
False
Question. If (AB)’ = B’ A’, where A and B are not square matrices, then number of rows in A is equal to number of columns in B and number of columns in A is equal to number of rows in B.
Answer
True
Question. (AB)-1 = A-1 · B-1, where A and B are invertible matrices satisfying commutative property with respect to multiplication.
Answer
True
Question. AA’ is always a symmetric matrix for any matrix A.
Answer
True
Question.
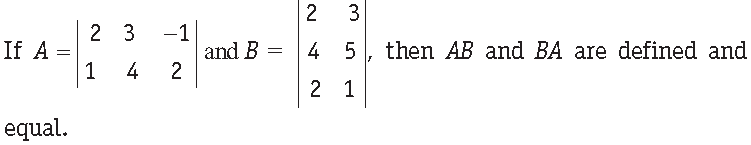
Answer
False
We hope you liked the above provided MCQ Questions Chapter 3 Matrices Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.


