Please refer to MCQ Questions Chapter 10 Gravitation Class 9 Science with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for Class 9 Science issued for the current academic year. We have provided MCQ Questions for Class 9 Science for all chapters on our website. Students should learn the objective based questions for Chapter 10 Gravitation in Class 9 Science provided below to get more marks in exams.
Chapter 10 Gravitation MCQ Questions
Please refer to the following Chapter 10 Gravitation MCQ Questions Class 9 Science with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 10 Gravitation Class 9 Science
Question. A projectile is projected with velocity kve in vertically upward direction from the ground into the space. (ve isescape velocity and k, < 1). If air resistance is considered to be negligible then the maximum height from the centre of earth to which it can go, will be : (R = radius of earth)
(a) R k2 + 1
(b) R k2 – 1
(c) R 1 – k2
(d) R k + 1
Answer
C
Question. The escape velocity for the earth is 11.2 km/sec. The mass of another planet is 100 times that of the earth and its radius is 4 times that of the earth. The escape velocity for this planet will be
(a) 112.0 km/s
(b) 5.6 km/s
(c) 280.0 km/s
(d) 56.0 km/s
Answer
D
Question. The escape velocity from the surface of earth is Ve . The escape velocity from the surface of a planet whose mass and radius are 3 times those of the earth will be
(a) Ve
(b) 3Ve
(c) 9Ve
(d) 27Ve
Answer
A
Question. How much energy will be necessary for making a body of 500 kg escape from the earth 2 [g = 9.8 m / s2 , radius of earth = 6.4 x 106 m]
(a) About 9.8 x 106 J
(b) About 6.4 x 108 J
(c) About 3.1 x 1010 J
(d) About 27.4 x 1012 J
Answer
C
Question. Two bodies of masses 1 m and 2 m are initially at rest at infinite distance apart. They are then allowed to move towards each other under mutual gravitational attraction. Their relative velocity of approach at a separation distance r between them is
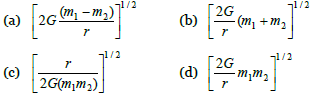
Answer
B
Question. The escape velocity of a planet having mass 6 times and radius 2 times as that of earth is
(a) √3 Ve
(b) 3 Ve
(c) √2 Ve
(d) 2 Ve
Answer
A
Question. A simple pendulum has a time period T1 when on the earth’s surface and T2 when taken to a height R above the earth’s surface, where R is the radius of the earth. The value of T2 / T1 is
(a) 1
(b) √2
(c) 4
(d) 2
Answer
D
Question. Orbital velocity of an artificial satellite does not depend upon
(a) Mass of the earth
(b) Mass of the satellite
(c) Radius of the earth
(d) Acceleration due to gravity
Answer
B
Question. Escape velocity on the earth
(a) Is less than that on the moon
(b) Depends upon the mass of the body
(c) Depends upon the direction of projection
(d) Depends upon the height from which it is projected
Answer
D
Question. If the gravitational force between two objects were proportional to 1/R (and not as 1 / R2) where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
(a) 1 / R2
(b) R0
(c) R1
(d) 1/R
Answer
B
Question. The time period of a geostationary satellite is
(a) 24 hours
(b) 12 hours
(c) 365 days
(d) One month
Answer
A
Question. An artificial satellite moving in a circular orbit around the earth has a total (kinetic + potential) energy 0 E . Its potential energy is
(a) -E0
(b) 1.5 E0
(c) 2 E0
(d) E0
Answer
C
Question. A geostationary satellite is revolving around the earth. To make it escape from gravitational field of earth, is velocity must be increased
(a) 100%
(b) 41.4%
(c) 50%
(d) 59.6%
Answer
B
Question. Pascal is a unit of
(a) pressure
(b) force
(c) linear momentum
(d) energy
Answer
A
Question. Gravitational force is a
(a) repulsive force
(b) attractive force
(c) neither (a) nor (b)
(d) both (a) and (b)
Answer
B
Question. A beaker is filled with a liquid of density r upto a height h . If the beaker is at rest, the mean pressure at the walls is
(a) 0
(b) h r g
(c) h r g/2
(d) 2h r g
Answer
C
Question. A coin and a feather are dropped together in a vacuum. Then
(a) the coin will reach the ground first
(b) the feather will reach the ground first
(c) both will reach the ground at the same time
(d) the feather will not fall down
Answer
C
Question. “When a solid body is partially or completely immersed in a fluid, the fluid exerts an upward force on the body, whose magnitude is equal to the weight of the displaced fluid”. This is known as
(a) Archimedes’ principle
(b) Tyndall effect
(c) Newton’s lst law of motion
(d) Bernoulli’s theorem
Answer
A
Question. Relative density of silver is 10.8. The density of water is 103 kg/m3 . What is the density of silver is SI units?
(a) 10.8 x 103 kg/m3
(b) 12.3 x 103 kg/m3
(c) 10.8 x 102 kg/m3
(d) 11.7 x 103 kg/m3
Answer
A
Question. A body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be
(a) mgR
(b) 1/2 mgR
(c) 2 mgR
(d) 1/4 mgR
Answer
B
Question. The distance of neptune and saturn from sun are nearly 13 10 and 12 10 meters respectively. Assuming that they move in circular orbits, their periodic times will be in the ratio
(a) √10
(b) 100
(c) 10√10
(d) 1 /√10
Answer
C
Question. A satellite of mass m is placed at a distance r from the centre of earth (mass M). The mechanical energy of the satellite is
(a) – GMm/r
(b) GMm/r
(c) GMm/2r
(d) – GMm/2r
Answer
D
Question. A satellite moves around the earth in a circular orbit of radius r with speed v. If the mass of the satellite is M, its total energy is
(a) -1/2 Mv2
(b) 1/2 Mv2
(c) 3/2 Mv2
(d) Mv2
Answer
A
Question. If acceleration due to gravity on the surface of a planet is two times that on surface of earth and its radius is double that of earth. Then escape velocity from the surface of that planet in comparison to earth will be
(a) 2 ve
(b) 3 ve
(c) 4 ve
(d) None of these
Answer
A
Question. Given mass of the moon is 1/81 of the mass of the earth and corresponding radius is 1/4 of the earth. If escape velocity on the earth surface is 11.2 km/s, the value of same on the surface of the moon is
(a) 0.14 km/s
(b) 0.5 km/s
(c) 2.5 km/s
(d) 5 km/s
Answer
C
Question. If the radius of a planet is R and its density is ρ , the escape velocity from its surface will be
(a) ve ∝ pR
(b) ve ∝ √pR
(c) ve ∝ √p/R
(d) ve ∝ 1/√pR
Answer
B
Question. The angular velocity of rotation of star (of mass M and radius R) at which the matter start to escape from its equator will be
(a) √2GM2 / R
(b) √2GM / g
(c) √2GM / R3
(d) √2GM / M
Answer
C
Question. The least velocity required to throw a body away from the surface of a planet so that it may not return is (radius of the planet is 6.4 x 106 m, g = 9.8 m / sec2)
(a) 9.8 x 10-3 m/sec
(b) 12.8 x 103 m/sec
(c) 9.8 x 103 m/sec
(d) 11.2 x 103 m/sec
Answer
D
Question. The escape velocity of a body on an imaginary planet which is thrice the radius of the earth and double the mass of the earth is (ve is the escape velocity of earth)
(a) √2 / 3 ve
(b) √3 / 2 ve
(c) √2/3 ve
(d) 2 / √3 ve
Answer
A
Question. The escape velocity on earth is 11.2 km/s. On another planet having twice radius and 8 times mass of the earth, the escape velocity will be
(a) 3.7 km/s
(b) 11.2 km/s
(c) 22.4 km/s
(d) 43.2 km/s
Answer
C
Question. Escape velocity on earth is 11.2 km/s. What would be the escape velocity on a planet whose mass is 1000 times and radius is 10 times that of earth
(a) 112 km/s
(b) 11.2 km/s
(c) 1.12 km/s
(d) 3.7 km/s
Answer
A
Question. The escape velocity for a body projected vertically upwards from the surface of earth is 11 km/s. If the body is projected at an angle of 45°with the vertical, the escape velocity will be
(a) 11/√2 km/s
(b) 11√2 km/s
(c) 22 km/s
(d) 11 km/s
Answer
D
Question. The acceleration due to gravity on a planet is same as that on earth and its radius is four times that of earth. What will be the value of escape velocity on that planet if it is ve on earth
(a) ve
(b) 2ve
(c) 4ve
(d) ve / 2
Answer
B
Question. Four particles each of mass M, are located at the vertices of a square with side L. The gravitational potential due to this at the centre of the square is
(a) – √32 GM/L
(b) – √64 GM/L2
(c) Zero
(d) √32 GM/L
Answer
A
Question. The ratio of the radii of planets A and B is k1 and ratio of acceleration due to gravity on them is k2 . The ratio of escape velocities from them will be
(a) k1k2
(b) √k1k2
(c) √k1 / k2
(d) √k2 / k1
Answer
B
Question. The escape velocity of a body on the surface of the earth is 11.2 km/s. If the earth’s mass increases to twice its present value and the radius of the earth becomes half, the escape velocity would become
(a) 5.6 km/s
(b) 11.2 km/s (remain unchanged)
(c) 22.4 km/s
(d) 44.8 km/s
Answer
C
Question. Consider a satellite going round the earth in an orbit. Which of the following statements is wrong
(a) It is a freely falling body
(b) It suffers no acceleration
(c) It is moving with a constant speed
(d) Its angular momentum remains constant
Answer
B
Question. The period of a satellite in a circular orbit around a planet is independent of
(a) The mass of the planet
(b) The radius of the planet
(c) The mass of the satellite
(d) All the three parameters (a), (b) and (c)
Answer
C
Question. If a satellite is orbiting the earth very close to its surface, then the orbital velocity mainly depends on
(a) The mass of the satellite only
(b) The radius of the earth only
(c) The orbital radius only
(d) The mass of the earth only
Answer
B
Question. A mass of 6 x 1024 kg is to be compressed in a sphere in such a way that the escape velocity from the sphere is 3 x 108 m /s. Radius of the sphere should be
(G = 6.67 x 10-11 N – m2 / kg2)
(a) 9 km
(b) 9 m
(c) 9 cm
(d) 9 mm
Answer
D
Question. There are two planets. The ratio of radius of the two planets is K but ratio of acceleration due to gravity of both planets is g. What will be the ratio of their escape velocity
(a) (Kg)1 / 2
(b) (Kg)-1 / 2
(c) (Kg)2
(d) (Kg)-2
Answer
A
Question. If ve and vo represent the escape velocity and orbital velocity of a satellite corresponding to a circular orbit of radius R, then
(a) ve = vo
(b) √2vo = ve
(c) ve = vo /2v
(d) ve and vo are not related
Answer
B
Question. If r represents the radius of the orbit of a satellite of mass m moving around a planet of mass M, the velocity of the satellite is given by
(a) v2 = g M/r
(b) v2 = GMm/r
(c) v = GM/r
(d) v2 = GM/r
Answer
D
Question. Which is constant for a satellite in orbit
(a) Velocity
(b) Angular momentum
(c) Potential energy
(d) Acceleration
(e) Kinetic energy
Answer
B
Question. Select the correct statement from the following
(a) The orbital velocity of a satellite increases with the radius of the orbit
(b) Escape velocity of a particle from the surface of the earth depends on the speed with which it is fired
(c) The time period of a satellite does not depend on the radius of the orbit
(d) The orbital velocity is inversely proportional to the square root of the radius of the orbit
Answer
D
Question. The distance of a geo-stationary satellite from the centre of the earth (Radius R = 6400 km) is nearest to
(a) 5 R
(b) 7 R
(c) 10 R
(d) 18 R
Answer
B
Question. A satellite which is geostationary in a particular orbit is taken to another orbit. Its distance from the centre of earth in new orbit is 2 times that of the earlier orbit. The time period in the second orbit is
(a) 4.8 hours
(b) 48 √2 hours
(c) 24 hours
(d) 24 √2 hours
Answer
B
Question. Potential energy of a satellite having mass ‘m’ and rotating at a height of 6.4 x 106 m from the earth surface is
(a) -0.5 mgRe
(b) -mgRe
(c) -2 mgRe
(d) -4 mgRe
Answer
A
Question. The ratio of the K.E. required to be given to the satellite to escape earth’s gravitational field to the K.E. required to be given so that the satellite moves in a circular orbit just above earth atmosphere is
(a) One
(b) Two
(c) Half
(d) Infinity
Answer
B
Question. If Gravitational constant is decreasing in time, what will remain unchanged in case of a satellite orbiting around earth
(a) Time period
(b) Orbiting radius
(c) Tangential velocity
(d) Angular velocity
Answer
C
Question. The distance between centre of the earth and moon is 384000 km. If the mass of the earth is kg 6 x 1024 and G = 6.66 x 10-11 Nm2 /kg2 . The speed of the moon is nearly
(a) 1 km/sec
(b) 4 km/sec
(c) 8 km/sec
(d) 11.2 km/sec
Answer
A
Question. An earth satellite of mass m revolves in a circular orbit at a height h from the surface of the earth. R is the radius of the earth and g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by
(a) gR2/R + h
(b) gR
(c) gR/R + h
(d) √gR2/R + h
Answer
D
Question. The earth revolves about the sun in an elliptical orbit with mean radius 9.3 x 107 m in a period of 1 year. Assuming that there are no outside influences
(a) The earth’s kinetic energy remains constant
(b) The earth’s angular momentum remains constant
(c) The earth’s potential energy remains constant
(d) All are correct
Answer
B
Question. Venus looks brighter than other planets because
(a) It is heavier than other planets
(b) It has higher density than other planets
(c) It is closer to the earth than other planets
(d) It has no atmosphere
Answer
C
Question. An astronaut orbiting the earth in a circular orbit 120 km above the surface of earth, gently drops a spoon out of space-ship. The spoon will
(a) Fall vertically down to the earth
(b) Move towards the moon
(c) Will move along with space-ship
(d) Will move in an irregular way then fall down to earth
Answer
C
Question. The velocity with which a projectile must be fired so that it escapes earth’s gravitation does not depend on
(a) Mass of the earth
(b) Mass of the projectile
(c) Radius of the projectile’s orbit
(d) Gravitational constant
Answer
B
Question. A small satellite is revolving near earth’s surface. Its orbital velocity will be nearly
(a) 8 km/sec
(b) 11.2 km/sec
(c) 4 km/sec
(d) 6 km/sec
Answer
A
Question. A satellite revolves around the earth in an elliptical orbit. Its speed
(a) Is the same at all points in the orbit
(b) Is greatest when it is closest to the earth
(c) Is greatest when it is farthest from the earth
(d) Goes on increasing or decreasing continuously depending upon the mass of the satellite
Answer
B
Question. The orbital velocity of an artificial satellite in a circular orbit just above the earth’s surface is v. For a satellite orbiting at an altitude of half of the earth’s radius, the orbital velocity is
(a) 3/2 v
(b) √3/2 v
(c) √2/3 v
(d) 2/3 v
Answer
C
Question. For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is
(a) 2
(b) 1 / 2
(c) 1 / √2
(d) √2
Answer
B
Question. The radius of a planet is 1/4 of earth’s radius and its acceleration due to gravity is double that of earth’s acceleration due to gravity. How many times will the escape velocity at the planet’s surface be as compared to its value on earth’s surface
(a) 1/√2
(b) √2
(c) 2√2
(d) 2
Answer
A
Question. If the earth is at one-fourth of its present distance from the sun, the duration of the year will be
(a) Half the present year
(b) One-eighth the present year
(c) One-fourth the present year
(d) One-sixth the present year
Answer
B
Question. A planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1 . At another point Q, when it is farthest from the sun at a distance d2 , its speed will be

Answer
C
Question. The orbital speed of Jupiter is
(a) Greater than the orbital speed of earth
(b) Less than the orbital speed of earth
(c) Equal to the orbital speed of earth
(d) Zero
Answer
B
Question. Choose the correct statement from the following : The radius of the orbit of a geostationary satellite depends upon
(a) Mass of the satellite, its time period and the gravitational constant
(b) Mass of the satellite, mass of the earth and the gravitational constant
(c) Mass of the earth, mass of the satellite, time period of the satellite and the gravitational constant
(d) Mass of the earth, time period of the satellite and the gravitational constant
Answer
D
Question. Two satellites of masses m1 and m2 (m1 > m2) are revolving round the earth in circular orbits of radius r1 and r2 (r1 > r2) respectively. Which of the following statements is true regarding their speeds v1 and v2 ?
(a) v1 = v2
(b) v1 < v2
(c) v1 > v2
(d) v1 / r1 = v2 / r2
Answer
B
Question. In a satellite if the time of revolution is T, then K.E. is proportional to
(a) 1/T
(b) 1/T2
(c) 1/T3
(d) 1/T-2/3
Answer
D
Question. A particle of mass 10 g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle far away from the sphere (you may take G = 6.67 x 10-11 Nm2 / kg2
(a) 6.67 x 10-9 J
(b) 6.67 x 10-10 J
(c) 13.34 x 10-10 J
(d) 3.33 x 10-10 J
Answer
B
Question. When a satellite going round the earth in a circular orbit of radius r and speed v loses some of its energy, then r and v change as
(a) r and v both with increase
(b) r and v both will decrease
(c) r will decrease and v will increase
(d) r will decrease and v will decrease
Answer
C
Question. An earth satellite S has an orbit radius which is 4 times that of a communication satellite C. The period of revolution of S is
(a) 4 days
(b) 8 days
(c) 16 days
(d) 32 days
Answer
B
Question. Out of the following, the only incorrect statement about satellites is
(a) A satellite cannot move in a stable orbit in a plane passing through the earth’s centre
(b) Geostationary satellites are launched in the equatorial plane
(c) We can use just one geostationary satellite for global communication around the globe
(d) The speed of a satellite increases with an increase in the radius of its orbit
Answer
D
Question. A satellite is moving around the earth with speed v in a circular orbit of radius r. If the orbit radius is decreased by 1%, its speed will
(a) Increase by 1%
(b) Increase by 0.5%
(c) Decrease by 1%
(d) Decrease by 0.5%
Answer
B
Question. The weight of an astronaut, in an artificial satellite revolving around the earth, is
(a) Zero
(b) Equal to that on the earth
(c) More than that on the earth
(d) Less than that on the earth
Answer
A
Question. In the following four periods
(i) Time of revolution of a satellite just above the earth’s surface (Tst)
(ii) Period of oscillation of mass inside the tunnel bored along the diameter of the earth (Tma)
(iii) Period of simple pendulum having a length equal to the earth’s radius in a uniform field of 9.8 N/kg (Tsp)
(iv) Period of an infinite length simple pendulum in the earth’s real gravitational field (Tis)
(a) Tst > Tma
(b) Tma > Tst
(c) Tsp < Tis
(d) Tst = Tma = Tsp = Tis
Answer
C
Question. The escape velocity for the earth is ve . The escape velocity for a planet whose radius is four times and density is nine times that of the earth, is
(a) 36 ve
(b) 12 ve
(c) 6 ve
(d) 20 ve
Answer
B
Question. If the height of a satellite from the earth is negligible in comparison to the radius of the earth R, the orbital velocity of the satellite is
(a) gR
(b) gR/2
(c) √g / R
(d) √gR
Answer
D

We hope you liked the above provided MCQ Questions Chapter 10 Gravitation Class 9 Science with solutions. If you have any questions please ask us in the comments box below.
