Please see Light Reflection and Refraction Class 10 Science Revision Notes provided below. These revision notes have been prepared as per the latest syllabus and books for Class 10 Science issues by CBSE, NCERT, and KVS. Students should revise these notes for Chapter 10 Light Reflection and Refraction daily and also prior to examinations for understanding all topics and to get better marks in exams. We have provided Class 10 Science Notes for all chapters on our website.
Chapter 10 Light Reflection and Refraction Class 10 Science Revision Notes
Reflection of Light by Spherical Mirrors
Light travels in a straight line and can change its direction when incident on a shiny surface.
Jatin looks inside a polished steel bowl and gets surprised to find his face appearing inverted inside the bowl. Furthermore, the image of his face changes its size as the bowl is moved towards or away from him. However, when he looks on the outer side of the same bowl, he finds his image to be erect. Why does this happen? This happens because the curved surface of the bowl acts as special kind of mirror, known as a spherical mirror. A spherical mirror can be made from a spherical ball.

There are two types of spherical mirrors
i) Concave mirrors
ii) Convex mirrors
Concave mirrors

A concave mirror is a spherical mirror whose reflecting surface is curved inwards. In a concave mirror, reflection of light takes place from the inner surface. This mirror resembles the shape of a ‘cave’. A Painted surface is a non-reflecting surface.
Convex mirrors
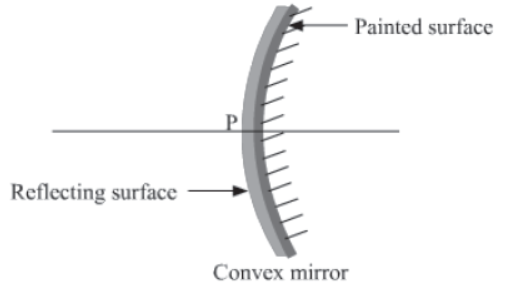
A convex mirror is a spherical mirror whose reflecting surface is curved outwards. In a convex mirror, the reflection of light takes place from its outer surface. A Painted surface is a non-reflecting surface.
Hence, the inward surface of the steel bowl or a spoon acts as a concave mirror, while its outer surface acts as a convex mirror.
There are some definitions associated with spherical mirrors, which will prove helpful in the discussion of spherical mirrors. But, before going into the definitions, let us understand the terms clearly.
So, the definitions of the terminologies are as follows:

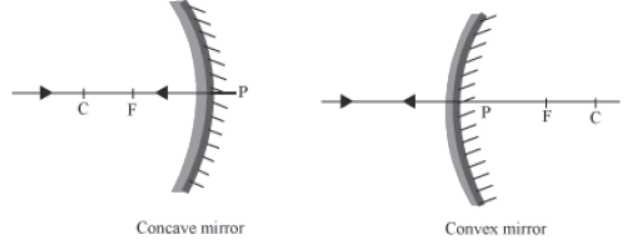
Pole of a spherical mirror
The central point of the reflecting surface of a spherical mirror is termed as the pole. It lies on the mirror and is denoted by the letter (P).
Centre of curvature
The centre of curvature as the centre of a sphere from which the given spherical mirror (convex or concave) is obtained. It is denoted by the letter (C).
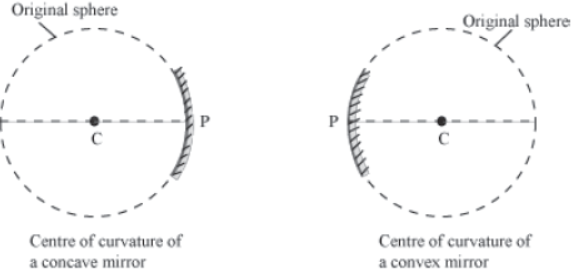
Radius of curvature
The distance between the centre of curvature and pole (PC) is known as the radius of curvature.
Principal axis of the spherical mirror
The imaginary straight line passing through the pole (P) and the centre of curvature (C) is termed as the principal axis.

Focus
The focus (F) is the point on the principal axis of a spherical mirror where all the incident rays parallel to the principal axis meet or appear to diverge from after reflection.
For concave mirrors, the focus lies on the same side of the reflecting surface.
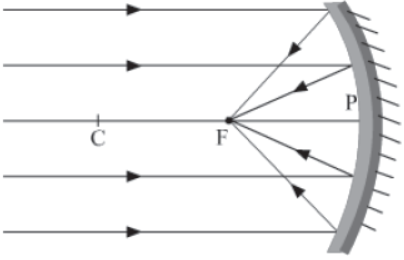
For convex mirrors, the focus is obtained on the opposite side of the reflecting surface by extrapolating the rays reflected from the mirror surface.

Radius of curvature (R) and the focal length (f) of a spherical mirror are related as R = 2f
Where, R is the distance between the centre of curvature and the pole of the mirror,
while f is the distance between the focus and the pole of the mirror.
The focus of a spherical mirror always lies between the pole (P) and the centre of curvature (C).
Reflection by spherical mirrors
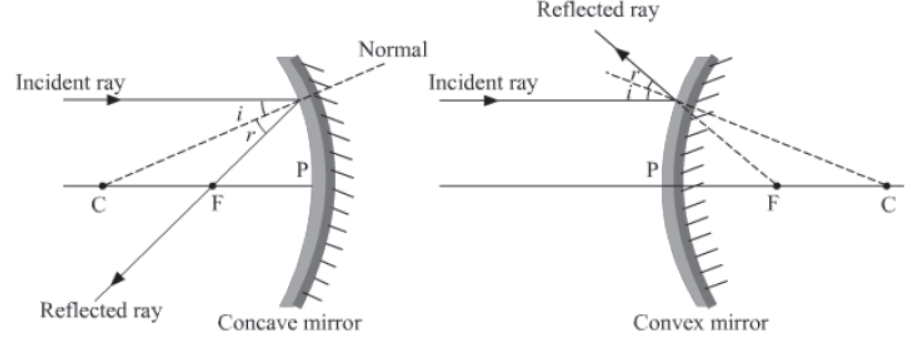
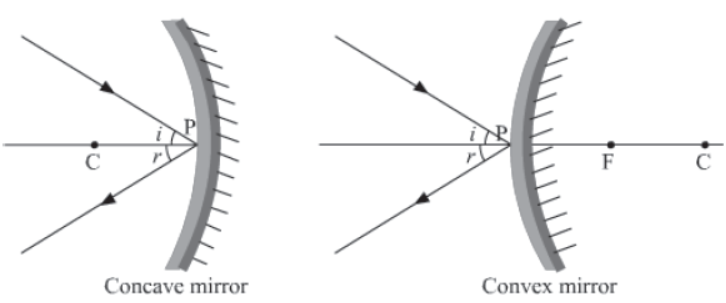
The laws of reflection are also followed by spherical mirrors, same as the plane mirrors.
The laws of reflection are:
1) The angle of incidence of light is always equal to angle of reflection of light.
2) The incident ray, the normal and the reflected ray, all lie in the same plane.
The different ways in which a ray of light is reflected from a spherical mirror are:
Case I: When the incident light ray is parallel to the principal axis.
In this case, the reflected ray will pass through the focus of a concave mirror, or it appears to pass through the focus of a convex mirror.
Case II: When the incident light ray passes through the focus of a concave mirror, or appears to pass through the focus of a convex mirror.
In this case, the reflected light will be parallel to the principal axis of the spherical mirror.

Case III: When the incident ray passes through or appears to pass through the centre of curvature.
In this case, light after reflecting from the spherical surface moves back in the same path.
This happens because light is incident perpendicularly on the mirror surface.

Case IV: When the incident ray is normal to the reflecting surface
In this case, the incident light ray will be reflected back by the reflecting surface of the spherical mirror, as in the case of plane mirror.
Case V: When the ray incident obliquely to the principal axis.
In this case, the incident ray will be reflected back by the reflecting surface of the spherical mirror obliquely. And making equal angles with the principal axis.
Four spherical mirrors of radius of curvature R1, R2, R3, and R4 (R1 > R3 > R2 > R4) are placed against the sunlight. Try to obtain the bright spot on a paper sheet for each mirror. Which mirror forms the brightest spot at a maximum distance from the pole of the mirror? Explain.
Do You Know:
Radio telescope is a reflecting telescope that tends to reflect all parallel rays coming from distant stars, galaxies, deep space etc. to a single point. This is because the reflecting surface acts as a large concave mirror. The point where the reflected rays meet is its focus. A receiver is placed at the focus, which receives light rays and sends these rays to a computer in the form of electrical signals. As a result, images of a light source can be obtained on the monitor.

Images Formed by Spherical Mirrors
Images formed by spherical mirrors
Spherical mirrors form images of an object that may be smaller, larger, or of the same size, erect or inverted, depending on their type and their distance from the object. In general, images formed by any type of mirrors can be classified in two types: real images and virtual images.
Difference between a real image and a virtual image
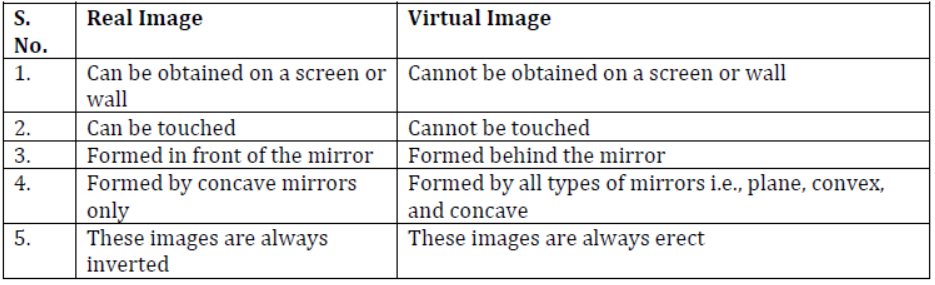
You can distinguish between real and virtual images by checking the orientation (erect or inverted) of images and also by touching them.
Let us learn about the images formed by different spherical mirrors.
So, you have seen that
- the image formed by a convex mirror is virtual, erect, and of a smaller size.
- the image formed by a concave mirror is virtual, erect and of a larger size when placed near the surface of the mirror; and inverted and may be smaller or larger than the object when placed at a distance from the surface.
Concave mirrors form larger, smaller and of same size real images and also larger virtual images. On the other hand, convex mirrors always form smaller virtual images.
Take a concave mirror and a sharpener. Now, try to see the image of the sharpener in the mirror. Make sure that the sharpener is at a large distance from the concave mirror. Observe the size and the orientation of the image. Now, reduce the distance between the sharpener and the mirror and again notice the size and the orientation of the image. Repeat the observation by reducing the distance and try to complete the following table.
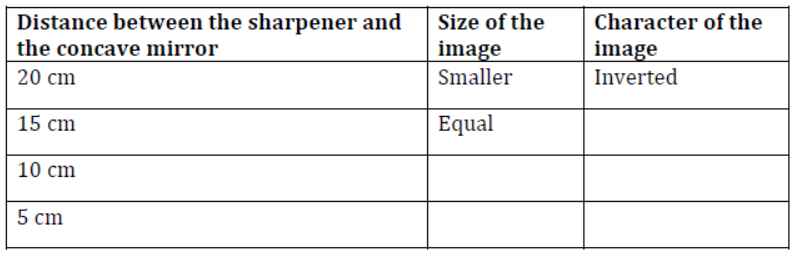
Replace the concave mirror with a convex mirror and follow the same steps. Make a similar table for the convex lens too.
Collect some objects that have shiny surfaces and classify them as plane, convex, or concave mirrors.
Reflection by Spherical Mirrors
The different ways in which a ray of light is reflected from a spherical mirror are as follows:
Case I: When the incident light ray is parallel to the principal axis
In this case, the reflected ray will pass through the focus of a concave mirror, or will appear to pass through the focus of a convex mirror.

Case II: When the incident light ray passes through the focus of a concave mirror, or appears to pass through the focus of a convex mirror
In this case, the reflected light will be parallel to the principal axis of the spherical mirror.
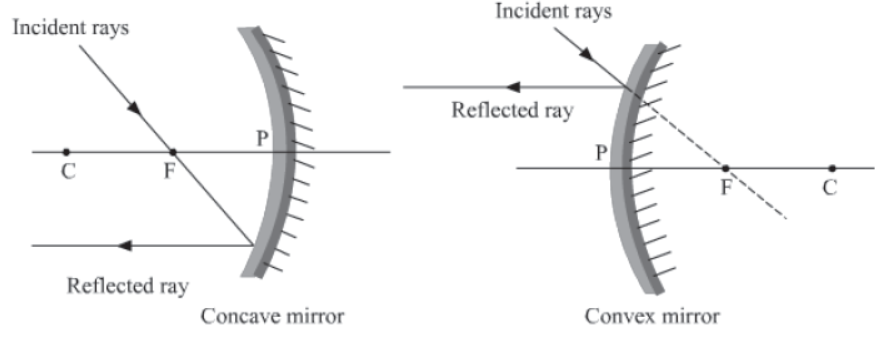
Case III: When the incident ray passes through or appears to pass through the centre of curvature
In this case, after reflecting from the spherical surface, light moves back in the same path.
This happens because light is incident perpendicularly on the mirror surface.
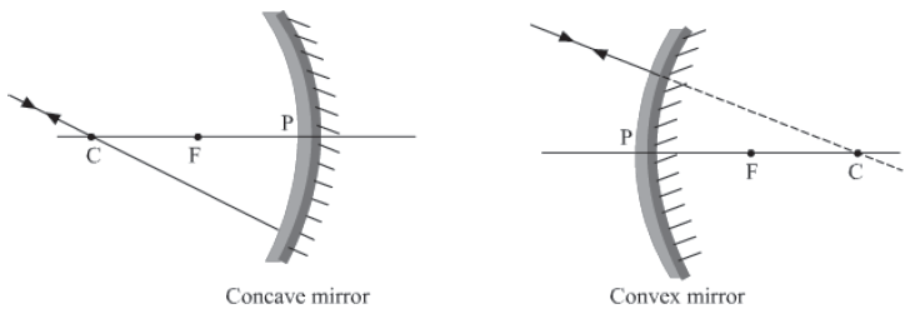
Case IV: When the incident ray is normal to the reflecting surface
In this case, the incident light ray will be reflected back by the reflecting surface of the spherical mirror, as in the case of a plane mirror.

Case V: When the ray incident obliquely to the principal axis.
In this case, the incident ray will be reflected back by the reflecting surface of the spherical mirror obliquely. And making equal angles with the principal axis.

Four spherical mirrors of radius of curvature R1, R2, R3 and R4 (R1 > R3 > R2 > R4) are placed against sunlight. A bright spot is obtained on a paper sheet for each mirror. Which mirror forms the brightest spot at a maximum distance from the pole of the mirror? Explain.
Images formed by Concave Mirrors
A concave mirror can produce both real and virtual images. The nature of an image depends primarily on the distance of the object from the mirror.
Let us consider the following cases:
I. When the object is at infinity
The light rays coming from infinity are parallel. When parallel light rays are incident on the reflecting surface of a concave mirror, they tend to meet at its focus after reflection. In this case, the image is formed at the focus, and is point-sized. It is also real and inverted.

II. When the object is behind the centre of curvature

In this case, the image is formed between the focus (F) and the centre of curvature (C). This image is real, inverted and diminished.
III. When the object is at the centre of curvature
In this case, the image is formed at the centre of curvature. This image is real, inverted and of the same size as the object.
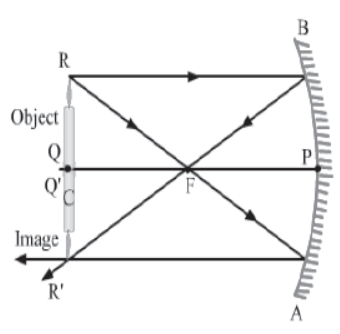
IV. When the object is between the centre of curvature (C) and the focus (F)

In this case, the image is formed behind the centre of curvature.
V. When the object is at the focus (F)
In this case, the image is formed at infinity. This image is real, inverted and highly enlarged.
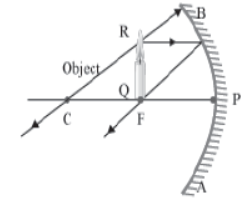
VI. When the object is placed between the focus (F) and the pole (P)

In this case, the image is formed behind the mirror. This image is virtual, erect and magnified.
The discussion is summarised in the table given below.


Images Formed by Convex Mirrors
A convex mirror always produces virtual and erect images of very small size. The images formed by a convex mirror are primarily classified in two ways.
I. When the object is at infinity
In this case, the image appears to form at the focus. This image is virtual, erect and very small in size.

II. When the object is between the pole (P) and a point X (X lies beyond C)
In this case, the image is formed between the pole (P) and the focus (F), behind the mirror.
This image is virtual, erect and small in size.

These results are summarised in the following table.


Uses of Spherical Mirrors

Sanjay went to a dentist’s clinic to get his decaying tooth examined. While sitting on the dentist’s chair, he observed that the doctor was using a special type of mirror to examine his tooth. He wondered why the dentist had to use a different mirror for the examination.

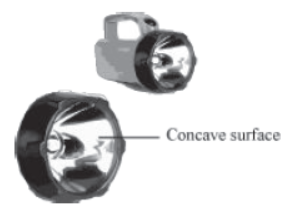
The special mirrors used by dentists are known as dentist’s mirror. This mirror is actually a concave mirror and thus, capable of producing a larger image of an object (teeth, in this case). In this section, we will discuss the uses of the properties of concave and convex mirrors in our daily life.
Concave mirror
A concave mirror has the capability of forming images that can be smaller or larger in size and virtual or erect, depending on the position of the object.
These mirrors are used in various medical practices. For example, doctors use this mirror for obtaining a relatively larger image of teeth, ear, skin etc.
Concave mirrors are also used in reflectors for torches and headlights in vehicles. This is because these mirrors can reflect rays of light beams as very powerful light rays.
Convex mirror
A convex mirror always produces a smaller, virtual, and erect image of an object.
In convex mirror, the length of the image is shorter than that of the object. Hence, it is used as a side view mirror in vehicles because the viewed area must be larger than the surface area of the mirror. The convex mirror forms images of vehicles that are spread over a relatively larger area.

Vehicle mirror
Owing to this property, convex mirrors are also used in security mirrors that we often see in shops, malls, etc.

Sign Convention in the Mirror Formula and Magnification
Amit takes a concave mirror of radius of curvature of 30 cm. He places a candle 22 cm away from its reflecting surface. Now, he wants to find out the correct position of the image. How can he find out its correct position?

To solve such problems, we use a set of sign conventions applicable for reflection of light by spherical mirrors. These conventions are known as the New Cartesian Sign Conventions. Here, the pole (P) of the mirror is considered as the origin.
Sign Conventions for spherical Mirrors :
I. Objects are always placed to the left of the mirror i.e. light must fall on the mirror from left to right.
II. All distances are measured from the pole of the mirror.
III. Distances along the direction of the incident ray (along positive x- axis) are taken as positive, while distances along the direction of the reflected ray (along negative x-axis) are taken as negative.
IV. Heights measured perpendicular to and above the principal axis (along positive y-axis) are taken as positive.
V. Heights measured perpendicular to and below the principal axis (along negative y-axis) are taken as negative.
These sign conventions can also represented in the following diagram:

Mirror formula
- The distance of an object from the pole of a mirror is termed as the object distance denoted by ‘u’.
- The distance of an image from the pole of a mirror is termed as the image distance denoted by ‘v’.
The formula relating the object distance (u), image distance (v), and the focal length (f) of a spherical mirror is given by:

The following table summarizes the sign conventions for concave and convex mirrors.

Magnification
Take a spherical mirror and place an object in front of it. Try to observe the image formed by the mirror. You will observe that the height of the image changes as the object is moved towards or away from the pole.
This change in height and position of the image by changing the object position gives the magnification of a spherical mirror. The magnification of a spherical mirror gives the relative extent to which the image of an object is magnified with respect to the object size.
Magnification is expressed by the ratio of the image height (HI) to the object height (HO).
Magnification (m) =


This equation holds true for both concave and convex mirrors.
Also, magnification remains the same for virtual and real images.
Magnification produced by a plane mirror is +1. Can you explain why?
Example: A convex mirror is used as a safety mirror in a shop. It has a focal length of 15 m.
A person is standing 12 m away from this mirror. Find the position of his image.
Solution:

For the given convex mirror,
Using sign conventions
Focal length (f) = + 15 m
Object distance (u) = – 12 m
Image distance (v) =?
On applying the mirror formula, we get

Therefore, the image is formed 6.67 m behind the mirror.
Example: An object of height 6 cm is placed 18 cm away from a concave mirror. The image is formed 12 cm before the mirror. Find out the following:
(i) Focal length of the mirror (f)
(ii) Radius of curvature (R)
(iii) Image height (HI)
(iv) Magnification of the mirror (m)
Solution:
For the given concave mirror,
Using sign conventions
Object distance (u) = – 18 cm
Image distance (v) = – 12 cm
Height of object (H0)= 6 cm
Focal length (f) =?
Radius of curvature =?
Image height =?
Magnification =?
(i) On applying the mirror formula, we get
Thus, the focal length of the given concave mirror is 7.2 cm.

Thus, the focal length of the given concave mirror is 7.2 cm.
(ii) Radius of curvature is given by
R = 2f
= 2 × 7.2 = 14.4 cm
Thus, the radius of curvature is 14.4 cm.
(iii) Magnification (m) = -v/u
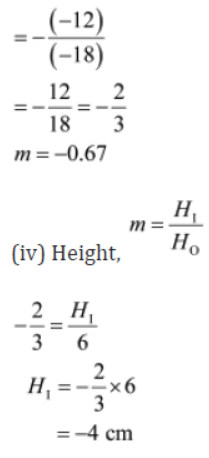
Here, the negative sign indicates that the image formed is real and inverted.
Hence, height of the image is 4 cm.
Laws of Refraction
Laws of refraction
There are two laws of refraction.
First law of refraction
The incident ray, the refracted ray, and the normal to the interface of two media at the
point of incidence – all lie in the same plane.
Second law of refraction
The ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant, for the light of a given color and for given pair of media. This is known as Snell’s law. Mathematically, it can be given as follows:

Here, is the relative refractive index of medium b with respect to medium a.
aμb
So, what are the key points of the experiment?
- When a light ray enters from air (rarer medium) to glass (denser medium), it bends towards the normal.
- When a light ray emerges from the glass (denser medium) to air (rarer medium), it bends away from the normal.
Hence, when a light ray is incident on a rectangular glass slab, the light emerges parallel to the incident ray from the opposite side of the slab.
And when a light ray is incident on a glass slab normally, it gets out straight without any deflection i.e., i = 0, r = 0.
Example: A ray of light is incident on a glass surface in such a way that it makes an angle of 60° with the normal (as shown in the given figure). Determine the angle of refraction (Given that the relative refractive index, μ= 1.34).
Solution:
Angle of incidence, i = 60°
Angle of refraction, r =?
Using Snell’s law of refraction,


= 400
Hence, the angle of refraction is approx. 40°.
Relation between refractive index of a medium and the speed of light
The refractive index of a medium (μμ) and the speed of light in it are related as:


Refraction of Light by Spherical Lenses (Concave And Convex)
Ankit went to an optician and noticed different types of spectacles there. He observed that while the glasses of some spectacles were relatively thicker in the middle, other glasses were thicker on the edge. The glasses of these spectacles are examples of lenses.
A lens is a transparent material bound by two curved surfaces. Lenses are broadly classified into two categories depending on their surfaces.

However, we will discuss only double spherical lenses here.
Convex lens
A convex lens is made by joining two spherical surfaces in such a way that it is thicker at the centre. Its thickness gradually reduces as we move towards the edge.


A convex lens has the ability to converge the light rays to a point that are incident on it.
Thus, it is called a converging lens.
Concave lens
A concave lens is made by joining two curved surfaces in such a way that it is thinner at the centre. Its thickness gradually increases as we move towards the edge.
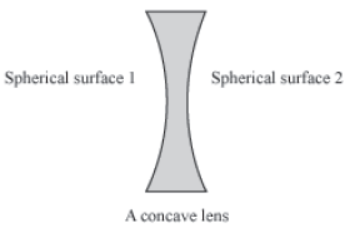
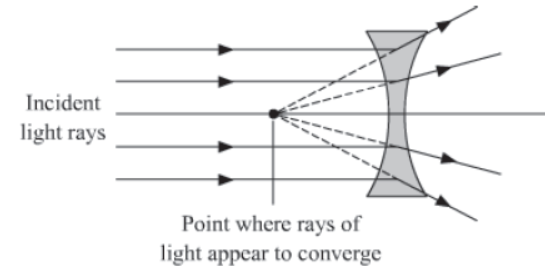
A concave lens has the ability to diverge a beam of light rays incident on it. Thus, it is called a diverging lens.
Differences between a spherical mirror and a lens
The following table lists some common differences between spherical mirrors and lenses

The second difference arises due to the fact that a lens has two spherical surfaces (i.e. it can be made from the arc of two spheres of equal radius).Therefore, light is refracted twice before it comes out of the lens.
Terms Associated with Lenses:

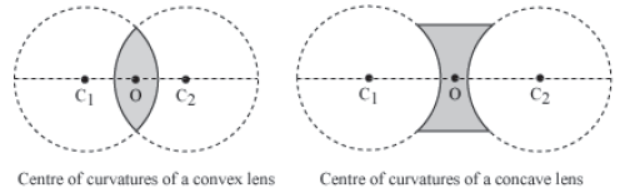
Optical centre
Optical centre is a point at the centre of the lens. It always lies inside the lens and not on the surface. It is denoted by ‘O’.
Centre of curvature
It is the centre point of arcs of the two spheres from which the given spherical lens (concave or convex) is made. Since a lens constitutes two spherical surfaces, it has two centers of curvature.
The distance of the optical centre from either of the centre of curvatures is termed as the radius of curvature.
Principal axis
The imaginary straight line joining the two centers of curvature and the optical centre (O) is called the principal axis of the lens.

Hold a convex lens and direct it against the sunlight. You will find a bright spot appear on the wall. Can you explain the formation of this bright spot? Light, after refracting through the lens, converges at a very sharp point. Try to obtain the brightest possible spot. Now, place a paper on the wall and observe what happens in the next few minutes.
Focus
The focus (F) is the point on the principal axis of a lens where all incident parallel rays, after refraction from the lens meet or appear to diverge from. For lenses there are two foci (F1 and F2) depending on the direction of incident rays.
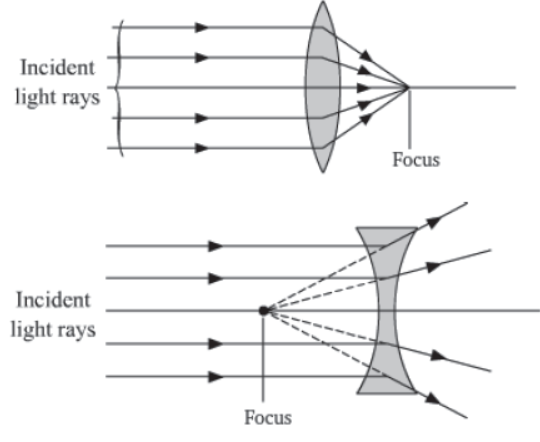
The distance between the focus (F1 or F2) and the optical centre (O) is known as the focal length of the lens.
Refraction by Spherical Lenses
Refraction by a spherical lens can be categorized into three cases.
Case I. When the incident light ray is parallel to the principal axis
In this case, the refracted ray will pass through the second focus F2 for a convex lens, and appear to diverge from the first focus F1 for a concave lens.

Case II. When the incident light ray emerges from the first focus F1 of a convex lens, or appears to emerge from the second focus F2 of a concave lens
In this case, light after refraction from both the lenses will move parallel to the principal axis.

Case III. When the light ray passes through the optical centre (O) of a lens
In this case, the light ray will pass through both the lenses without suffering any deviation.
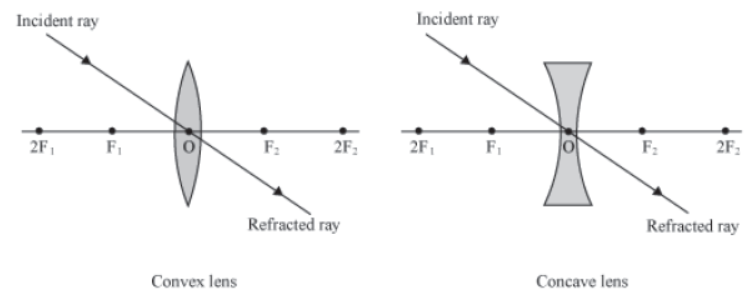
Image Formed by Spherical Lenses

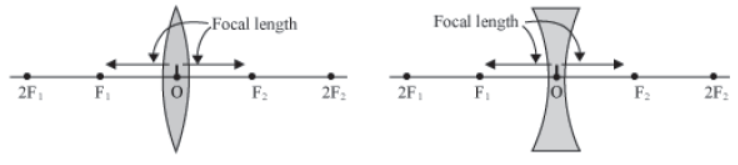
Take a convex lens of known focal length. Draw five equidistant points on a table and put the lens on the central line. Mark the lines as 2F1, F1, O, F2, 2F2 (as shown in the figure).
Take a candle and placed it behind 2F1. Observe the nature and size of the image formed on a screen placed on the other side of the lens. An inverted image of the candle flame can be seen easily. Now, repeat the process by changing the position of the candle by bringing it towards the lens, and list your observations.
Lenses are able to form images by refracting incident light rays. Although, a light source emits infinite number of light rays in all possible directions, we will consider only two light rays for the sake of convenience. It allows us to show clearly the nature and position of the image formed on a screen.
Images Formed by a Convex Lens
A convex lens can produce real as well as virtual images. The nature of the images formed depends primarily on the position of the object on the principal axis.
Consider the following cases:
The ray diagrams for all the cases are as follows:
I. When the object is at infinity.

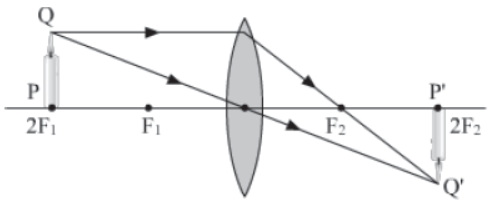
II. When the object is beyond the centre of 2F1.

III. When the object is at the centre of curvature 2F1.
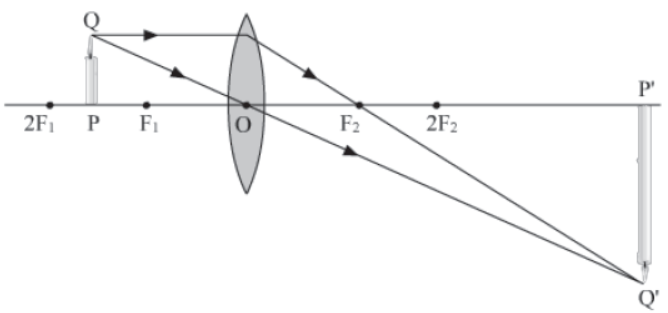
IV. When the object is placed between the focus F1 and 2F1.
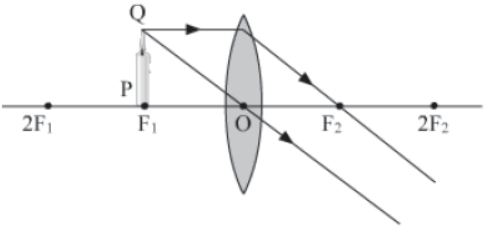
V. When the object is placed at focus F1.
VI. When the object is placed between the focus F1 and optical centre O.
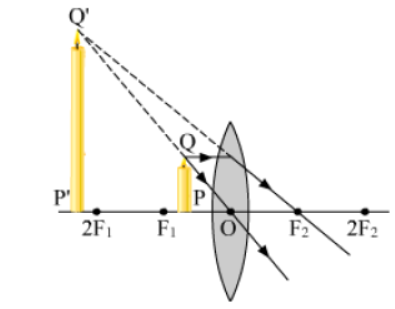
The position, size, and nature of the image formed by a convex lens can be summarized in the table below.

Images Formed by a Concave Lens
A concave lens always produces virtual and erect images that are extremely small in size.
The images formed by a concave lens are divided into two cases.
The ray diagrams for all the cases are as follows:
I. When the object is placed at infinity.
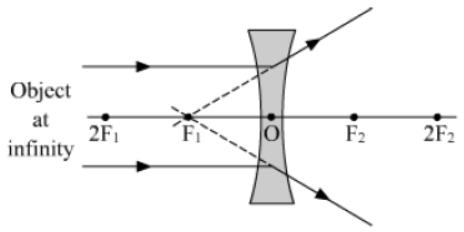
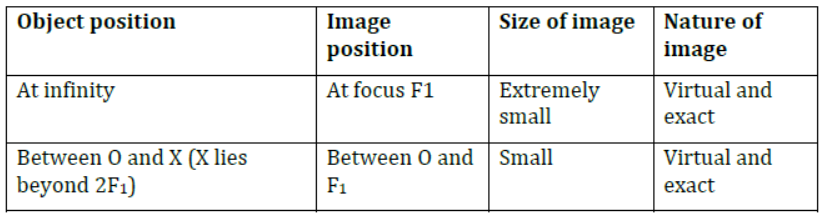
II. When the object is placed beyond 2F1.

The position, size, and nature of the image formed can be summarized in the table as follows:
Jai places a sharp edge in front of a spherical lens. He observes that the image formed is inverted and extremely small in size. Can you guess the nature of the lens used and the position of the edge? Where should he place this edge to obtain an erect image?
Lens Formula, Magnification, and Power
Usually in image formation, we are interested in calculating the distance of the image formed from the lens, size of the image, power of the lens etc. These problems can be solved with the help of a lens formula. For this, we use a set of sign conventions applicable for refraction of light by spherical lenses. In this convention, the optical centre (O) is treated as the origin.
Sigh Convention for Lenses
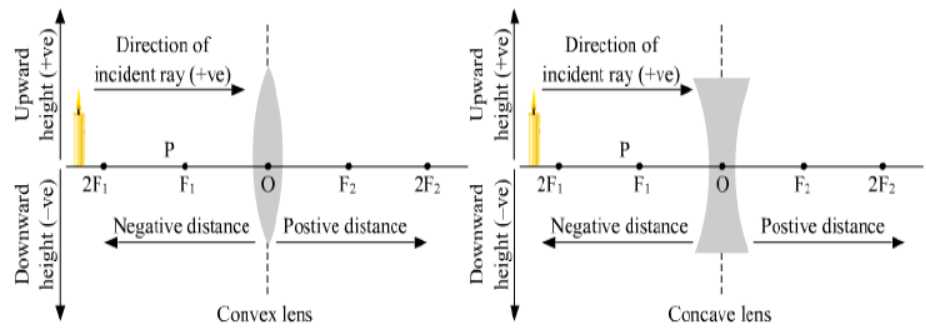
I. Object is always placed to the left of the lens i.e., the light must fall on the lens from left to right.
II. All distances parallel to the principal axis are measured from the optical centre of the lens.
III. Distances along the direction of incident rays (along positive x-axis) are taken as positive, while distances opposite to the direction of incident rays (along negative x-axis) are taken as negative.
IV. Distances measured above the principal axis (along positive y-axis) are taken as positive.
V. Distances measured below the principal axis (along negative y-axis) are taken as negative.
These sign conventions are represented in the following diagram:
A Concave lens always forms a virtual image.
Lens Formula:
The lens formula is given by
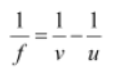
Here,
f → focal length of the spherical lens
v→ distance of the image from the optical centre
u → distance of the object from the optical centre

The apparent change in the size of the object is because of the magnification produced by the lens.
Magnification
The magnification of a spherical lens gives the relative extent to which the image of an object is magnified with respect to the object size.
Magnification is expressed by the ratio of the image height (HI) to the object height (HO).

Magnification (m) is also related to the object distance (u) and image distance (v) by the relation


Hence, the magnification formula can be written as
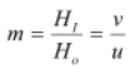
If magnification is positive, the image will be virtual and erect.
If magnification is negative, the image will be real and inverted.
Power of a Lens
The degree of converge/diverge a beam of light rays by a lens is expressed in terms of its power (P). It is the inverse of focal length, f (in metres).
Hence, power of a lens is given by the relation

The SI unit of power is dioptre (D).
Power of Combination of Thin Lenses in Contact
When two or more lenses are placed in contact with each other the net power (P) of the combination is given by the algebraic sum of the individual powers of the lenses.
Net power, P = P1 + P2 + P3 + …
Example 1: A convex lens has a focal length of 10 cm. If the image produced by it is 15 cm behind from the optical centre, then determine the distance at which the object is placed?
Also, find the magnification produced by the lens.
Solution:
For the given convex lens,
Focal length (f) = 10 cm
Image distance (v) = 15 cm
Object distance (u) =?
Using the lens formula:
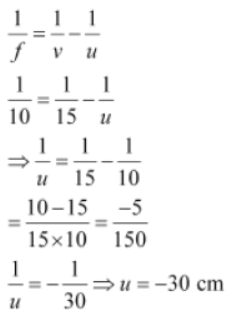
Here, the negative sign indicates that the object was placed to the left of the lens.
Now magnification, m = v/u
= 15/-30
= -0.5
Hence, the image size will be half of the object size. The negative sign of magnification implies that the image formed is real and inverted.
What will be the image distance if an object is placed at a distance of 30 cm before a concave lens of focal length 10 cm?
Example 2: What is the power of a convex mirror whose focal length is 25 cm?
Solution:
Power = 1 / f(In meters)
Given that focal length, f = 25 cm

Hence, power of the given lens is 4 D.
Note that if the lens was concave, then the focal length would have been, f = −25 cm = −0.25 m
In this case, power will be −4 D.


