Please refer to the Force And Laws Of Motion Revision Notes given below. These revision notes have been designed as per the latest NCERT, CBSE and KVS books issued for the current academic year. Students will be able to understand the entire chapter in your class 9th Science book. We have provided chapter wise Notes for Class 9 Science as per the latest examination pattern.
Revision Notes Chapter 9 Force And Laws Of Motion
Students of Class 9 Science will be able to revise the entire chapter and also learn all important concepts based on the topic wise notes given below. Our best teachers for Grade 9 have prepared these to help you get better marks in upcoming examinations. These revision notes cover all important topics given in this chapter.
We have learnt about the motion of objects based on the definition of displacement, velocity and acceleration. Now let us see the causes that influence the motion of bodies. Have you wondered why certain natural phenomena occur and why they continue to occur in the same way? For instance – why do the planets move around the Sun and why a ball thrown up comes back to the Earth? There is a force, which controls the motion of objects. We shall learn about that.
Force and Motion
A vegetable vendor applies force to push the cart, a driver applies force either to stop the car or to change the speed or direction of motion and a football player kicks the ball to set it in motion.
In all the above examples, the force applied on a body can bring about the following changes:
• It can change the state of rest of a body or change its position
• It can change the speed of the body
• It can change the direction of motion of a body
A Boy Hitting a Ball
Force is the external agent that changes the state of rest or uniform motion of a body along a straight line.
Resultant Force
Any object can be made to move by the application of force. Many forces can act simultaneously on a body. For example, several people can jointly move a boulder but a strong person can move the same boulder all by himself. That is, the force applied by the strong man produces the same effect as that produced by the net force applied by all. The force applied by the strong man is the resultant force.
The resultant force is that single force which when acting on a body produces the same effect as that produced by a number of forces.

Several people can jointly move a boulder
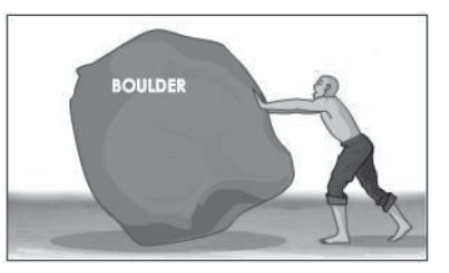
Strong person moving the same boulder all by himself
Resultant Force
F = F1 + F2 + F3 + F4
Balanced and Unbalanced Forces
The figures show a block of wood on a table. When the block is pulled at point A, it begins to move towards the left and if the block is pulled at the point B it moves towards the right.
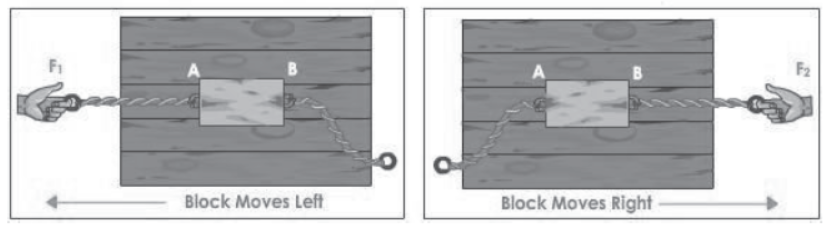
Example of Unbalanced Forces
But if the block is pulled from both sides with the same effort the block remains stationary. The forces are equal and opposite and therefore the block does not move. The resultant of the forces acting on the body is zero.
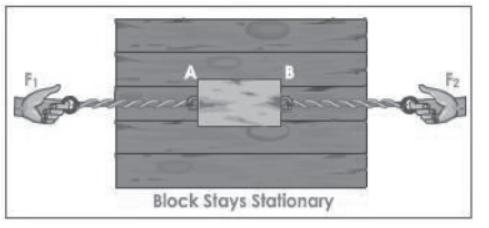
Example of Balanced Forces
In a game of tug of war when both the teams pull the rope with equal and opposite forces, then the rope remains stationary as the forces acting on it are equal and opposite and their resultant is zero.
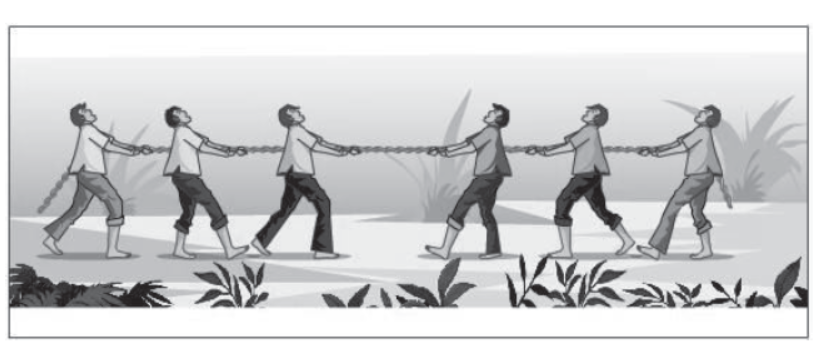
Example of Balanced Forces
Squeeze a rubber ball between the palms of your hands. What do you observe? The shape of the rubber ball changes. The forces applied on the ball are equal and opposite and the resultant of these forces does not move the object, instead the object gets deformed as long as the force is applied.
This is a temporary deformation.
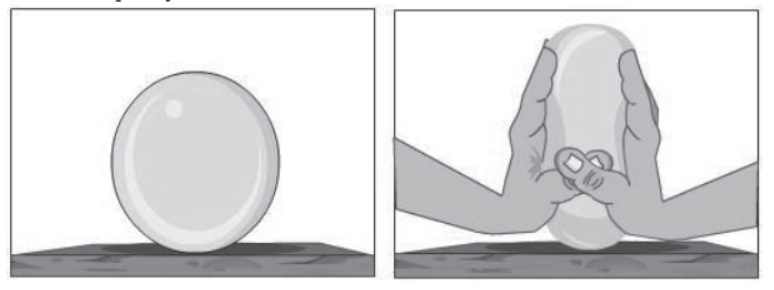
Deformation of a Spherical Ball by Unbalanced Forces
Hammer a piece of nail, it gets permanently deformed.
From the above examples we can conclude that if the forces acting on an object are equal and opposite then they do not change the state of rest of the object or uniform motion along a straight line, but they can deform the object. These types of forces which do not cause any change in state of rest or of uniform motion along a straight line are called balanced forces. The resultant of balanced forces is always equal to zero (because the forces are equal and opposite).
In tug of war, usually the weaker team is pulled by the other team, which is stronger. In this case, the forces are not equal and opposite i.e., they are not balanced and hence the weaker team is pulled by the stronger team.
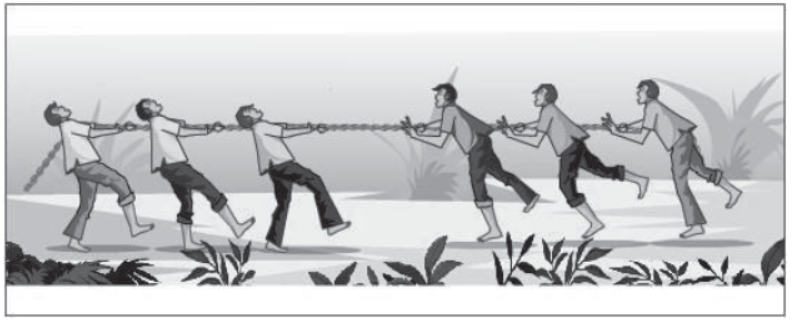
Unbalanced Forces
All of us know that when we stop pedaling a bicycle, the speed of the bicycle decreases due to the action of friction, which is the only force acting on the bicycle. Thus, if the forces acting on a body produce any change in state of rest or motion, then the forces are said to be unbalanced. An unbalanced force acting on an object changes its speed or direction. The resultant of unbalanced forces is always greater than zero.
Galileo’s Observation and Origin of Newtonian Mechanics
Aristotle and other medieval thinkers believed that the natural state of bodies is the state of rest.
Galileo opposed this concept.
Galileo observed that, when a ball was made to roll down an inclined plane, its speed increased.
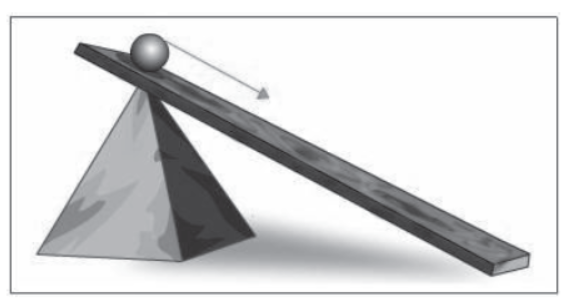
An Object Moving Down an Inclined Plane with Increasing Speed
Similarly, when it was made to roll up the inclined plane, its speed decreased.

An Object Moving Upward with Decreasing Speed
He then tried rolling it on a horizontal plane. Galileo repeated this experiment by making the surface very smooth. He observed that the ball continued to move for a longer time. Galileo
suggested that the speed of the ball moving on a horizontal plane would remain constant in the absence of an external force or force of friction.
Galileo suggested that the natural tendency of all bodies is to oppose a change in their state of rest or motion.

An Object Moving Along a Horizontal Plane
Force and Laws of Motion
Inertia
It is clear from Galileo’s experiments that all objects have a tendency to continue in their state of rest or of uniform motion until an external force acts on it. The following examples will help to understand the observations of Galileo’s experiment.
Place a cardboard on an empty tumbler and a coin on the cardboard as shown in the figure.
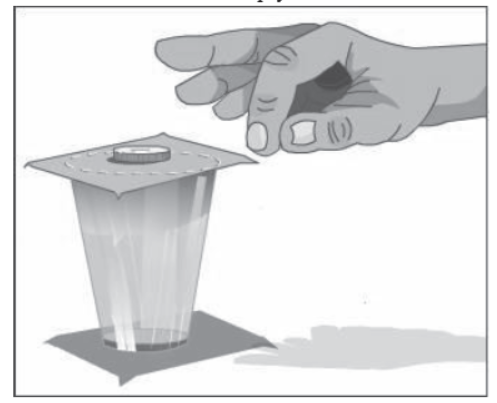
Cardboard and a Coin placed on an Empty Tumbler
Flick the cardboard with the finger. What do you observe? The coin drops into the tumbler. When we flick the cardboard the cardboard moves fast whereas the coin continues in its state of rest and hence drops into the tumbler.

Coin Drops into the Tumbler as the Cardboard is Flicked
A passenger standing in a moving bus leans forward when the brakes are applied all of a sudden. This is because the body of the passenger is in motion along with the bus. When the bus stops all of a sudden, the lower part of his body comes to rest along with the bus whereas the upper part of the body continues to move forward.
From the above examples it is clear that objects continue to remain in their state of rest or of uniform motion until an external force is applied. This tendency of an object to resist any change in its state of rest or of uniform motion is called inertia.
Inertia can be defined as the property of matter by virtue of which it opposes any change in its state of rest or of uniform motion along a straight line.
Inertia is classified as:
• Inertia of rest
• Inertia of motion
• Inertia of direction
Examples of Inertia of Rest
• A passenger standing in a bus leans backwards when the bus starts all of a sudden
• Fruits fall down when the branches of a tree are shaken
• Dust particles on a carpet falls when we beat the carpet with a stick
Examples of Inertia of Motion
• A passenger standing in a moving bus leans forward when the bus stops all of a sudden
• A man carelessly alighting from a moving train leans forward
Example of Inertia of Direction
• The water particles sticking to the cycle tyre are found to fly off tangentially
• Whenever a driver is negotiating a curve, the passengers experience a force acting away from the centre of the curve
Inertia of a body depends upon its mass. That is, massive objects possess more inertia than lighter ones.
Newton’s First Law of Motion
We shall now study about the exact relation between the force applied and the motion of the object on which the force is applied. This was studied by Sir Issac Newton. He gave the three basic laws of motion concerning objects in motion.
Sir Isaac Newton formulated Galileo’s observations into a law. This law is known as Newton’s first
law of motion.
A body continues to be in a state of rest or of uniform motion along a straight line unless an external force acts upon it.
This means that every object has a tendency to resist any change in its state of rest or motion. This tendency is inertia. This law is also known as law of inertia.
Newton’s first law of motion gives a qualitative definition of force.
Momentum
A cricket ball and a tennis ball are moving with a constant velocity v. You have to apply more force to stop the cricket ball than you have to apply to stop the tennis ball, since the mass of the cricket ball is more than that of the tennis ball.
The force required to stop a moving object depends on the mass of the body.
Now, suppose you have to stop two cricket balls A and B moving with velocities v1 and v2 respectively (v1 > v2) then you have to exert a greater force on A, because it is moving with a
greater velocity.
The force required to stop a moving body is directly proportional to its velocity. Thus the quantity of motion in a body depends on mass and velocity of the body. This quantity of motion
defines a new physical quantity called momentum.
The momentum of an object is defined as the product of its mass and its velocity. Momentum is a vector quantity and its direction will be same as that of velocity. It is represented by p.
p = mv where, m is the mass of the object, v is its velocity.
SI unit of momentum is kg m/s.
Note
p = mv. SI unit of mass is kg and SI unit of velocity is m/s.
Unit of momentum p is kg m/s
Newton’s Second Law of Motion
Newton’s second law of motion states that rate of change of momentum is directly proportional to applied force and takes place in the same direction as the applied force.
Explanation
Momentum is the force possessed by a body at any particular instant during its course of motion.
Mathematically momentum is the product of mass and velocity.
Consider a body of mass m, having an initial velocity u. Let the body be acted upon by some force
F for time t, such that its final velocity is v.
• Initial momentum = mu
Final momentum = mv
• Change in momentum in time t = m (v – u)
Change in momentum in unit time = m (v−u)/t
But v−u/t = a (acceleration)
• Change in momentum in unit time = ma
OR
Rate of change of momentum = ma
According to Newton’s second law
Rate of change of momentum F
• F m.a
F = K m.a (K is the constant of proportionality)
If a body has unit mass and unit acceleration, such that force possessed by it is also one unit then
1 = K × 1 × 1
or K = 1
• F = ma
Force = mass × acceleration
[The negative sign indicates that the gun is recoiling]
Rocket Propulsion Unit of Force
Recall that F = ma
We know that SI unit of mass is kg and acceleration is m/s2.
SI unit of force is kg m/s2. But 1kgm/s2 is defined as 1 Newton in honor of Sir Isaac Newton.
1 N = 1 kg m/s2
One Newton force is that force which produces an acceleration of 1 m/s2 on an object of mass 1
kg.
Force is a vector quantity
Newton’s second law of motion gives a quantitative definition of force.
Impulse
Mathematical representation of Newton’s second law of motion is
F = mv−mu/ t
Or
Ft = mv – mu
When the time of application of force is short then Ft is defined as impulse. Impulse is large force acting for a short duration.
SI unit of impulse = N s or kg m/s.
When we kick a football, the kick lasts only for a fraction of a second. The force, which we apply on a football, is an example for impulsive force.
Newton’s Third Law of Motion
Imagine that you are watching a volleyball match and suddenly the ball comes towards you. Due to your reflexes you hit the ball so that you do not get hurt. The ball moves away from you due to the action of your hand on it. But definitely your hands pain due to the impact of the ball. That is, whenever two bodies interact with each other, each exerts a force on the other. The force exerted by one of the two bodies is called the action force while the force exerted by the other is called the reaction force.
In the above example the force exerted by you on the ball is the action force and the force exerted by the ball on your hand is the reaction force. Action and reaction forces act simultaneously but on different bodies. Let us find out why a rubber ball rebounds when it is thrown on a hard floor. It is due to the action and reaction forces that are acting simultaneously.
The ball exerts a force (action force) on the floor and the floor exerts an equal and opposite force (reaction force) on it. The rubber ball being light rebounds.
Based on such examples of action and reaction forces, Sir Isaac Newton gave the third law of motion “To every action there is an equal and opposite reaction”.
An Experiment to Prove Newton’s Third Law of Motion
Couple two spring balances A and B as shown in the figure. When we pull the balance B both the balances show the same reading indicating that both the action and reaction forces are equal and opposite. In this case, the pull of either of the two spring balances can be regarded as action and that of the other balance as the reaction.
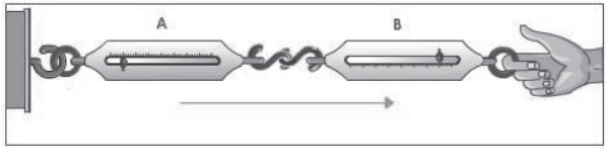
Two Spring Balances A and B Coupled Together
Let us now discuss some of the situations in daily life to illustrate Newton’s third law of motion.
• When we walk on the ground, then our foot pushes the ground backward (action force) and the ground in turn exerts a force on the foot (reaction force) pushing the foot forward
• When a man jumps from a diving board he pushes the board (action force) and the board in turn pushes the man forward in the opposite direction (reaction force)
• The birds, while flying, push the air downwards with the help of their wings (action force) and the air in turn exerts a force on the bird in the upward direction (reaction force)

A Bird in Flight
• A swimmer pushes the water in the backward direction (action force) and the water exerts a force on the swimmer (reaction force) which pushes him forward
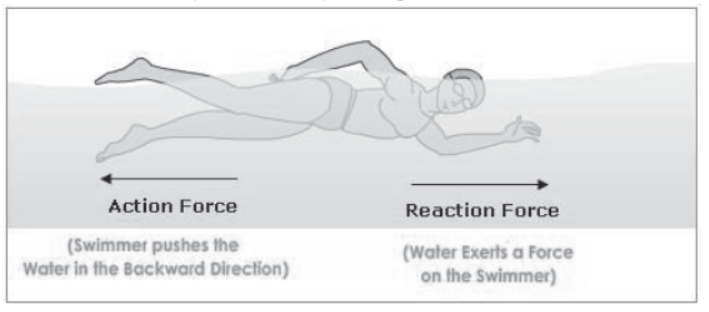
Action and Reaction Forces Acting on a Swimmer
Even though the action and reaction forces are equal and opposite their resultant is not equal to zero as the action and reaction forces are acting on two different bodies
• The third law holds good when the interacting bodies are at rest or in motion
• Newton’s third law describes the relationship between the force of interaction between two objects
• This law does not give us the magnitude of force
Law of Conservation of Momentum
From Newton’s third law of motion we know that whenever a force is applied on a body there will be an equal and opposite reaction. Action and reaction forces result in change in velocities of both the bodies which in turn change the momenta of these bodies.
In an elastic collision the initial momentum of the bodies before collision is found to be equal to the final momentum of the bodies after collision.
Thus Newton’s second and third laws of motion lead us to the very important law of mechanics, the law of conservation of momentum.
Law of conservation of momentum states that – if a group of bodies are exerting force on each other, i.e., interacting with each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them.
The following example will help us to understand clearly the law of conservation of momentum. Two bodies A and B of masses m1 and m2 are moving in the same direction with initial velocities u1 and u2. They make a direct collision. Let us assume that after collision they continue moving in the same direction. Let the collision last for a very short interval of time ‘t’ seconds.
During collision, A exerts a force on B. At the same time, B exerts a force on A. Due to these action and reaction forces the velocities of A and B get changed. After collision, let v1 and v2 be the velocities of the bodies A and B respectively.
The force exerted on A = m1 a1
[According to Newton’s II law of motion]
Acceleration produced in A = change in velocity/ time
a1 = v1−u1/ t
Therefore, force exerted on A = m1 (v1−u1 t )
F1= 𝑚1𝑣1−𝑚1𝑢1/ 𝑡
Acceleration produced in B = change in velocity/ time
F2 = v2−u2/ t
Therefore, force exerted on B = m2a2
= m2(v2−u2/ t )
= m2v2−m2u2/ t
According to Newton’s third law of motion, these two forces are equal and opposite.
i.e., F1 = −F2
m1v1−m1u1/ t = − [m2v2−m2u2/ t ]
m1v1 − m1u1 = −m2v2 + m2u2
i.e., total momentum before collision is equal to the total momentum after collision, which is nothing but law of conservation of momentum.
Applications of Law of Conservation of Momentum, Newton’s Third Law of Motion
Recoil of a Gun
When a bullet is fired from a gun, the gases produced in the barrel exerts a tremendous force on the bullet (action force). As a result, the bullet moves forward with a great velocity called the muzzle velocity. The bullet at the same time exerts an equal force on the gun in the opposite direction (reaction force). Due to this the gun moves backwards. This backward motion of the gun is called the recoil of the gun. The velocity with which the gun moves backwards is called the recoil velocity.
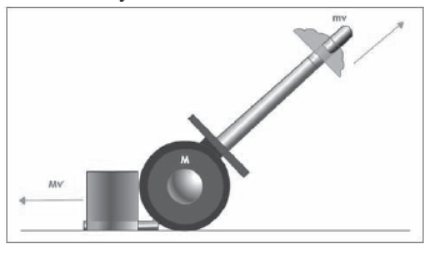
Let ‘M’ be the mass of the gun and m that of the bullet. Before firing both are at rest. After firing
let ‘V’ be the velocity of the gun and ‘v’ that of the bullet. By law of conservation of linear
momentum,
Initial momentum of gun and bullet = final momentum of gun and bullet.
The initial momentum of the gun and the bullet is equal to zero since they are initially at rest.
Final momentum after firing = MV + mv = 0
Or Re Coil Velocity V = − mv/ M
The motion of a rocket is an application of Newton’s third law of motion and law of conservation of linear momentum.
A rocket is a projectile that carries the rocket fuel and the oxidizer, which supplies the oxygen needed for combustion. Liquid hydrogen, liquid paraffin etc., are used as rocket fuels and hydrogen peroxide, liquid oxygen etc., are used as oxidizers. The fuel-oxidizer combination in a rocket is called the propellant.
The simplest form of a rocket consists of a combustion chamber in which a solid or liquid propellant is burnt. There is a nozzle at its tail through which the gaseous products of combustion can escape. The rocket forces a jet of hot gases downwards through the nozzle. This is the action. The jet of gases exerts an equal force on the rocket, pushing it forward. This is the reaction. This force gives the rocket a forward acceleration.

Rocket Propulsion
The operation of a rocket illustrates the conservation of momentum. Just before launching, the momentum of the rocket is zero. When the rocket is fired, it forces a jet of hot gases with a high velocity through the nozzle. The jet of gases acquires a momentum downwards. Hence, the rocket acquires a momentum of equal magnitude in opposite direction. Thus the rocket moves upwards. With a single stage rocket it is not possible to attain very high speed and hence multistage rockets are designed. In multistage rockets when the fuel of the first stage gets exhausted, the rocket casing is detached and dropped off and the second stage is ignited.



