VBQs Complex Numbers And Quadratic Equations Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Complex Numbers And Quadratic Equations Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Complex Numbers And Quadratic Equations VBQs Class 11 Mathematics
Question. Let α and β be the roots of the equation x2 – x – 1 = 0. If pk = (α)k + (β)k, k ≥ l, then which one of the following statements is not true ?
(a) p3 = p5 – p4
(b) P5 = 11
(c) (p1 + p2 + p3 + p4 + p5) = 26
(d) p5 = p2 × p3
Answer
D
Question. Let α and β be two real roots of the equation (k +1) tan2x – √2 . λ tan x = (1 – k), where k(≠ –1) and λ are real numbers. If tan2(α + β) = 50, then a value of λ is:
(a) 10√2
(b) 10
(c) 5
(d) 5√2
Answer
B
Question. Let z = x + iy be a non- ero complex number such that z2 = i |z|2, where i = √-1 , then z lies on the:
(a) line, y = –x
(b) imaginary axis
(c) line, y = x
(d) real axis
Answer
C
Question. If m is chosen in the quadratic equation (m2 + 1) x2 – 3x + (m2 + 1)2 = 0 such that the sum of its roots is greatest, then the absolute difference of the cubes of its roots is:
(a) 10√5
(b) 8√3
(c) 8√5
(d) 4√3
Answer
C
Question. The sum of the solutions of the equation | √x – 2 | + √x ( √x – 4) + 2 = 0, (x > 0) is equal to:
(a) 9
(b) 12
(c) 4
(d) 10
Answer
D
Question. If a and b are real numbers such that (2 + α)4 = α + bα, where α = (-1 + i√3) / 2 , then a + b is equal to :
(a) 9
(b) 24
(c) 33
(d) 57
Answer
A
Question. Let w (Im w ≠ 0) be a complex number. Then the set of all complex number z satisfying the equation w – w̅z = k (1 – z) , for some real number k, is
(a) { z : |z| = 1}
(b) { z : z = z̅ }
(c) { z : z ≠ 1}
(d) { z : |z| =1, z ≠ 1}
Answer
D
Question. Let α = Im( 1+z2 / 2iz ) , where z is any non- ero complex number.
The set A = {α : | z | = 1 and z ≠ ±1 } is equal to:
(a) (– 1, 1)
(b) [– 1, 1]
(c) [0, 1)
(d) (– 1, 0]
Answer
A
Question. Let Z and W be complex numbers such that |Z| = |W|, and arg Z denotes the principal argument of Z.
Statement 1: If arg Z + arg W = p, then Z = -w̅ .
Statement 2: |Z| = |W|, implies arg Z – arg w̅ = π.
(a) Statement 1 is true, Statement 2 is false.
(b) Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation for Statement 1.
(c) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation for Statement 1.
(d) Statement 1 is false, Statement 2 is true.
Answer
A
Question. The conjugate of a complex number is 1 / i–1 then that complex number is
(a) –1 / i –1
(b) 1 / i +1
(c) –1 / i +1
(d) 1 / i –1
Answer
C
Question. Let z0 be a root of the quadratic equation, x2 + x + 1 = 0. If z = 3 + 6i z081 – 3i z093, then arg z is equal to:
(a) π/4
(b) π/6
(c) π/3
(d) 0
Answer
A
Question. Let p, q and r be real numbers (p ≠ q, r ≠ 0), such that the roots of the equation 1/(x+p) + 1/(x+q) = 1/r are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to.
(a) p2 + q2 + r2
(b) p2 + q2
(c) 2 (p2 + q2)
(d) (p2 + q2) / 2
Answer
B
Question. If z = x -i y and 1/z3 = p + iq, then (x/p + y/q) / (p2+q2) is equal to
(a) –2
(b) –1
(c) 2
(d) 1
Answer
A
Question. Let and w be complex numbers such that z̅ + iw̅ = 0 and arg zw = π. Then arg equals
(a) 5π/4
(b) π/2
(c) 3π/4
(d) π/4
Answer
C
Question. Let
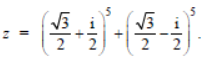
If R(z) and I(z) respectively denote the real and imaginary parts of z, then:
(a) I(z) = 0
(b) R(z) > 0 and I(z) > 0
(c) R(z) < 0 and I(z) > 0
(d) R(z) = – (c)
Answer
A
Question. The least positive integer n for which [ (1 + i√3) / (1 – i√3) ]n = 1, is
(a) 2
(b) 6
(c) 5
(d) 3
Answer
D
Question. If | – 4 | < | – 2 |, its solution is given by
(a) Re(z) > 0
(b) Re(z) < 0
(c) Re(z) > 3
(d) Re(z) > 2
Answer
C
Question. z and w are two non ero complex numbers such that | z | = | w| and Arg z + Arg w = π then equals

Answer
B
Question. Let Z1 and Z2 be two roots of the equation Z2 + aZ + b = 0 , Z being complex. Further , assume that the origin, Z1 and Z2 form an equilateral triangle. Then
(a) a2 = 4b
(b) a2 = b
(c) a2 = 2b
(d) a2 = 3b
Answer
D
Question. If p and q are the roots of the equation x2 + px + q = 0, then
(a) p = 1, q = –2
(b) p = 0, q = 1
(c) p = –2, q = 0
(d) p = – 2, q = 1
Answer
A
Question. The value of

(a) 1/2 (1-i√3)
(b) 1/2(√3 – i)
(c) – 1/2 (√3 – i)
(d) – 1/2 (1 – i√3)
Answer
C
Question. If z is a non-real complex number, then the minimum value of lmz5 / (lmz)5 is :
(a) –1
(b) –4
(c) –2
(d) –5
Answer
B
Question. If z is a complex number such that |z| ≥ 2, then the minimum value of | z + 1/2 |
(a) is strictly greater than 5/2
(b) is strictly greater than 3/2 but less than 5/2
(c) is equal to 5/2
(d) lie in the interval (1, 2)
Answer
D
Question. The imaginary part of (3 + 2√-54)½ – (3 – 2√-54)½ can be :
(a) – √6
(b) -2√6
(c) 6
(d) √6
Answer
B
Question. Let α = (-1 + i√3) / 2. if
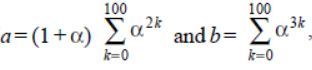
then α and b are the roots of the quadratic equation:
(a) x2 + 101x + 100 = 0
(b) x2 – 102 x + 101 = 0
(c) x2 – 101x + 100 = 0
(d) x2 + 102x +101 = 0
Answer
B
Question. If a ∈ R and the equation -3( x – [x] )2 + 2( x – [x] ) + α2 = 0 (where [x] denotes the greatest integer ≤ x ) has no integral solution, then all possible values of a lie in the interval:
(a) (-2,-1)
(b) (-∞,-2)υ(2,∞)
(c) (-1,0)υ(0,1)
(d) (1, 2)
Answer
C
Question. The values of ‘a’ for which one root of the equation x2 – (a + 1 ) x + a2 + a – 8 = 0 exceeds 2 and the other is lesser than 2, are given by :
(a) 3 < a < 10
(b) a ≥10
(c) -2 < a < 3
(d) a ≤ -2
Answer
C
Question. If the equations x2 + bx – 1 = 0 and x2 + x + b = 0 have a common root different from –1, then |b| is equal to :
(a) 2
(b) 3
(c) √3
(d) √2
Answer
C
Question. If λ ∈ R is such that the sum of the cubes of the roots of the equation, x2 + (2 – λ) x + (10 – λ) = 0 is minimum, then the magnitude of the difference of the roots of this equation is
(a) 20
(b) 2√5
(c) 2√7
(d) 4√2
Answer
B
Question. If both the roots of the quadratic equation x2 – 2kx + k2 + k – 5 = 0 are less than 5, then k lies in the interval
(a) (5, 6]
(b) (6, ∞ )
(c) (– ∞ , 4)
(d) [4, 5]
Answer
C
Question. The quadratic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is
(a) 1
(b) 4
(c) 3
(d) 2
Answer
D
Question. The least integral value α of x such that (x – 5) / (x2 + 5x – 14) > 0, satisfies :
(a) a2 + 3a – 4 = 0
(b) a2 – 5a + 4 = 0
(c) a2 – 7a + 6 = 0
(d) a2 + 5a – 6 = 0
Answer
A
Question. If equations ax2 + bx + c = 0 (a, b,c ∈ R,a ≠ 0) and 2x2 + 3x + 4 = 0 have a common root, then a : b : c equals:
(a) 1 : 2 : 3
(b) 2 : 3 : 4
(c) 4 : 3 : 2
(d) 3 : 2 : 1
Answer
B
Question. The value of k for which the equation (k – 2)x2 + 8x + k + 4 = 0 has both roots real, distinct and negative is
(a) 6
(b) 3
(c) 4
(d) 1
Answer
B
Question. Let for a ≠ 1 a ≠ 0, ƒ(x) = ax2 + bx + c, g(x) = a1x2 + b1x + c1 and p(x) = ƒ(x) – g(x).
If p(x) = 0 only for x = -1 and p (– 2) = 2, then the value of p(b) is :
(a) 3
(b) 9
(c) 6
(d) 18
Answer
D
Question. The equation √(3×2 + x 5) = x – 3 , where x is real, has;
(a) no solution
(b) exactly one solution
(c) exactly two solution
(d) exactly four solution
Answer
A
Question. If Re (z-1 / 2z+i) =1, where z = x + iy, then the point (x, y) lies on a:
(a) circle whose centre is at (- 1/2 , 3/2)
(b) straight line whose slope is – 2/3 .
(c) straight line whose slope is 3/2.
(d) circle whose diameter is √5/2.
Answer
D
Question. If Z1 ≠ 0 and Z2 be two complex numbers such that Z2 /z1 is a purely imaginary number, then | 2z1+3z2 / 2z1-3z2 | is equal to:
(a) 2
(b) 5
(c) 3
(d) 1
Answer
D
Question. | z1 + z2 |2 + | z1 – z2 |2 is equal to
(a) 2 ( | z1 + z2 | )
(b) 2 ( | z1 |2 + | z2 |2 )
(c) | z1 || z2 |
(d) | z1 |2 + | z2 |2
Answer
A
Question. Let
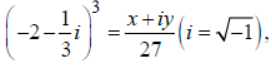
where x and y are real numbers then y – x equals :
(a) 91
(b) – 85
(c) 85
(d) – 91
Answer
A
Question. The point represented by 2 + i in the Argand plane moves 1 unit eastwards, then 2 units northwards and finally from there 2√2 units in the south–westwards direction. Then its new position in the Argand plane is at the point represented by :
(a) 1 + i
(b) 2 + 2i
(c) –2 – 2i
(d) –1 – i
Answer
A
Question. If x is a solution of the equation,
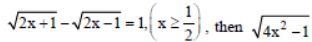
is equal to :
(a) 3/4
(b) 1/2
(c) 2√2
(d) 2
Answer
A
Question. Let α and β be the roots of equation x2 – 6x – 2 = 0. If an = αn – βn, for n ≥ 1, then the value of (a10 – 2a8) / 2a9 is equal to:
(a) 3
(b) – 3
(c) 6
(d) – 6
Answer
A
Question. A complex z number is said to be unimodular if |z| = 1. Suppose z1 and z2 are complex numbers such that (z1 – 2z2) / (2 – Z1z̅2) is unimodular and z2 is not unimodular. Then the point z1 lies on a:
(a) circle of radius 2.
(b) circle of radius √2.
(c) straight line parallel to x-axis
(d) straight line parallel to y-axis.
Answer
A
Question. If z ≠ 1 and z2 / (z – 1 ) is real, then the point represented by the complex number z lies :
(a) either on the real axis or on a circle passing through the origin.
(b) on a circle with centre at the origin
(c) either on the real axis or on a circle not passing through the origin.
(d) on the imaginary axis.
Answer
A
Question. If z = √3/2 + i/2 (i = √-1), then (1 + iz + z5 + iz8)9 is equal to:
(a) 0
(b) 1
(c) (– 1 + 2i)9
(d) – 1
Answer
D
Question. If ω = z/(z – 1/3 i) and |ω = 1, then z lies on
(a) an ellipse
(b) a circle
(c) a straight line
(d) a parabola
Answer
C
Question. If z1 and z2 are two non- ero complex numbers such that | z1 + z2 | = | z1 | + | z2 | , then arg z1 – arg z2 is equal to
(a) π/2
(b) – π
(c) 0
(d) -π/2
Answer
C
Question. If λ be the ratio of the roots of the quadratic equation in x, 3m2x2 + m(m – 4)x + 2 = 0, then the least value of m for which λ + 1/λ = 1, is :
(a) 2 – √3
(b) 4 – 3√2
(c) –2 + √2
(d) 4 – 2√3
Answer
B
Question. If one real root of the quadratic equation 81x2 + kx + 256 = 0 is cube of the other root, then a value of k is :
(a) –81
(b) 100
(c) 144
(d) – 300
Answer
D
Question. If the cube roots of unity are 1, ω, ω2 then the roots of the equation (x –1)3 + 8 = 0, are
(a) –1, –1 + 2 ω , – 1 – 2 ω2
(b) –1, – 1, – 1
(c) – 1, 1 – 2 ω , 1 – 2 ω2
(d) – 1, 1 + 2 ω , 1 + 2 ω2
Answer
C
Question. The product of the roots of the equation 9x2 – 18| x | + 5 = 0, is :
(a) 5/9
(b) 25/81
(c) 5/27
(d) 25/9
Answer
B
Question. If α and β are the roots of the quadratic equation, x2 + x sin θ – 2sinθ = 00, θ |∈ (0 , π/2), then
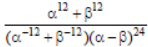
is equal to :
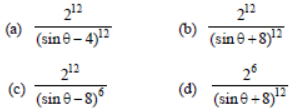
Answer
B
Question. The number of real roots of the equation 5 + | 2x – 1 | = 2x (2x – 2) is:
(a) 3
(b) 2
(c) 4
(d) 1
Answer
D
Question. If α and β are the roots of the equation, 7x2 – 3x – 2 = 0, the the value of α/(1 – α2) + β/(1 – β2) is equal to :
(a) 27/32
(b) 1/24
(c) 3/8
(d) 27/16
Answer
D
Question. If z is a complex number of unit modulus and argument θ, then arg( 1+z / 1+z̅ ) equals:
(a) –θ
(b) π/2 – θ
(c) π
(d) π – θ
Answer
C
Question. Let z satisfy| z | = 1 and = 1– z̅ .
Statement 1 : z is a real number.
Statement 2 : Principal argument of z is π/3
(a) Statement 1 is true Statement 2 is true; Statement 2 is a correct explanation for Statement 1.
(b) Statement 1 is false; Statement 2 is true
(c) Statement 1 is true, Statement 2 is false.
(d) Statement 1 is true; Statement 2 is true; Statement 2 is not a correct explanation for Statement 1.
Answer
B
Question. Let u = (2z + i) / (z – ki), z = x + iy and k > 0. If the curve represented by Re(u) + Im(u) = 1 intersects the y-axis at the points P and Q where PQ = 5, then the value of k is :
(a) 3/2
(b) 1/2
(c) 4
(d) 2
Answer
D
Question. If α and β are roots of the equation, x2 – 4√2kx + 2e4lnk – 1 = 0 for some k, and α2 + β2 = 66, then α3 + β3 is equal to:
(a) 248√2
(b) 280√2
(c) -32√2
(d) -280√2
Answer
D
Question. If 1/√α and 1/√β are the roots of the equation, ax2 + bx + 1 = 0 (a ≠ 0, a, b, ∈ R), then the equation, x( x+b3 ) ( a3 – 3abx ) 0 as roots :
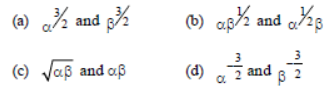
Answer
A
Question. Let λ ≠ 0 be in R. If α and β are roots of the equation, x2 – x + 2λ = 0 and α and γ are the roots of the equation, 3x2 – 10x + 27λ = 0, then βγ/λ is equal to :
(a) 27
(b) 18
(c) 9
(d) 36
Answer
B
Question. Let α and β be the roots of the equation, 5x2 + 6x – 2 = 0. If Sn = αn + βn, n = 1, 2,3, …, then :
(a) 6S6 + 5S5 = 2S4
(b) 6S6 + 5S5 + 2S4 = 0
(c) 5S6 + 6S5 = 2S4
(d) 5S6 + 6S5 + 2S4 = 0
Answer
C
Question. If the equation, x2 + bx + 45 = 0 (b ∈ R) has con ugate complex roots and they satisfy |z + 1| = 2√10 , then:
(a) b2 – b = 30
(b) b2 + b = 72
(c) b2 – b = 42
(d) b2 + b = 12
Answer
A
Question. Let p, q ∈ R. If 2 – √3 is a root of the quadratic equation, x2 + px + q = 0, then:
(a) p2 – 4q + 12 = 0
(b) q2 – 4p – 16 = 0
(c) q2 + 4p + 14 = 0
(d) p2 – 4q – 12 = 0
Answer
D
Question. If α and β be the roots of the equation x2 – 2x + 2 = 0, then the least value of n for which (α/β)n = 1 is :
(a) 2
(b) 5
(c) 4
(d) 3
Answer
C
Question. If the roots of the quadratic equation x2 + px + q = 0 are tan30° and tan15°, respectively, then the value of 2 + q – p is
(a) 2
(b) 3
(c) 0
(d) 1
Answer
B
Question. If z2 + z +1 = 0 , where is complex number, then the value of
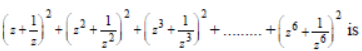
(a) 18
(b) 54
(c) 6
(d) 12
Answer
D
Question. Consider the quadratic equation (c – 5)x2 – 2cx + (c – 4) = 0, c ≠ 5. Let S be the set of all integral values of c for which one root of the equation lies in the interval (0, 2) and its other root lies in the interval (2, 3). Then the number of elements in S is:
(a) 18
(b) 12
(c) 10
(d) 11
Answer
D
Question. The value of λ such that sum of the squares of the roots of the quadratic equation, x2 + (3 – λ)x + 2 = l has the least value is:
(a) 15/8
(b) 1
(c) 4/9
(d) 2
Answer
D
Question. Difference between the corresponding roots of x2 + ax + b = 0 and x2 + bx + a = 0 is same and a ≠ b, then
(a) a + b + 4 = 0
(b) a + b – 4 = 0
(c) a – b – 4 = 0
(d) a – b + 4 = 0
Answer
A
Question. The value of a for which the sum of the squares of the roots of the equation x2 – (a – 2) x – a – 1 = 0 assume the least value is
(a) 1
(b) 0
(c) 3
(d) 2
Answer
A
Question. If |z – 4/z| = 2, then the maximum value of |z| is equal to :
(a) √5 +1
(b) 2
(c) 2 + √2
(d) √3 +1
Answer
A
Question. If | z – 3 + 2i | ≤ 4 then the difference between the greatest value and the least value of | z | is
(a) √13
(b) 2√13
(c) 8
(d) 4 + √13
Answer
B
Question. If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a,b,c ∈ R, have a common root, then a : b : c is
(a) 1 : 2 : 3
(b) 3 : 2 : 1
(c) 1 : 3 : 2
(d) 3 : 1 : 2
Answer
A
Question. If non- ero real numbers b and c are such that min f(x) > max g(x), where f(x) = x2 + 2bx + 2c2 and g(x) = – x2 – 2cx + b2 (x ∈ R); then c/b lies in the interval:
(a) (0 , 1/2)
(b) (1/2 , 1/√2)
(c) (1/√2 , √2)
(d) (√2 , ∞)
Answer
D
Question. If x is real, the maximum value of (3x2 + 9x +17) / (3x2 + 9x +7)
(a) 1/4
(b) 41
(c) 1
(d) 17/7
Answer
B
Question. If α ≠ β but α2 = 5α – 3 and β2 = 5β – 3 then the equation having α/β and β/α as its roots is
(a) 3x2 – 19x + 3 = 0
(b) 3x2 + 19x – 3 = 0
(c) 3x2 – 19x – 3 = 0
(d) x2 – 5x + 3 = 0.
Answer
A
Question. Let α and β be two roots of the equation x2 + 2x + 2 = 0, then α15 + β15 is equal to:
(a) – 256
(b) 512
(c) – 512
(d) 256
Answer
A
Question. If α and β be two roots of the equation x2 – 64x + 256 = 0. Then the value of (α3 / β5)1/8 + (β3 / α5)1/8 is:
(a) 2
(b) 3
(c) 1
(d) 4
Answer
A
Question. Let α, β be real and z be a complex number. If z2 + αz + β = 0 has two distinct roots on the line Re z =1, then it is necessary that :
(a) β ∈ (-1,0)
(b) |β| = 1
(c) β ∈ (1,∞)
(d) β ∈ (0,1)
Answer
C
Question. If α and β are the roots of the equation x2 – x + 1 = 0, then α2009 + β2009 =
(a) –1
(b) 1
(c) 2
(d) –2
Answer
B
Question. If α and β are the roots of the equation 2x(2x + 1) = 1, then β is equal to:
(a) 2a(a + 1)
(b) –2a(a + 1)
(c) 2a(a – 1)
(d) 2a2
Answer
B
Question. The number of all possible positive integral values of α for which the roots of the quadratic equation, 6x2 – 11x + α = 0 are rational numbers is:
(a) 3
(b) 2
(c) 4
(d) 5
Answer
A
Question. If | z2 -1|=| z |2 +1, then lies on
(a) an ellipse
(b) the imaginary axis
(c) a circle
(d) the real axis
Answer
B
Question. The locus of the centre of a circle which touches the circle | z – z1 | = α and | z – z2 | = b externally (z, z1 & z2 are complex numbers) will be
(a) an ellipse
(b) a hyperbola
(c) a circle
(d) none of these
Answer
B
Question. If both the roots of the quadratic equation x2 – mx + 4 = 0 are real and distinct and they lie in the interval [1, 5], then m lies in the interval:
(a) (– 5, – 4)
(b) (4, 5)
(c) (5, 6)
(d) (3, 4)
Answer
B
Question. If an angle A of a Δ ABC satisfies 5 cos A + 3 = 0, then the roots of the quadratic equation, 9x2 + 27x + 20 = 0 are.
(a) sin A, sec A
(b) sec A, tan A
(c) tan A, cos A
(d) sec A, cot A
Answer
B
Question. The number of real roots of the equation, e4x + e3x – 4e2x + ex + 1 = 0 is:
(a) 1
(b) 3
(c) 2
(d) 4
Answer
A
Question. The least positive value of ‘α’ for which the equation, 2x2 + (α – 10)x + 33/2 = 2α has real roots is _______.
Answer
8
Question. If tan A and tan B are the roots of the quadratic equation, 3x2 – 10x – 25 = 0 then the value of 3 sin2 (A + B) – 10 sin (A + B). cos (A + B) – 25 cos2 (A + B) is
(a) 25
(b) – 25
(c) – 10
(d) 10
Answer
B
Question. If, for a positive integer n, the quadratic equation,

has two consecutive integral solutions, then n is equal to:
(a) 11
(b) 12
(c) 9
(d) 10
Answer
A
Question. If (1- p) is a root of quadratic equation x2 + px + (1- p) = 0 then its root are
(a) –1, 2
(b) –1, 1
(c) 0, –1
(d) 0, 1
Answer
C
Question. The number of real solutions of the equation x2 – 3|x| + 2 = 0 is
(a) 3
(b) 2
(c) 4
(d) 1
Answer
C
Question. The sum of all the real values of x satisfying the equation 2(x-1)(x2+5x-50) = 1 is :
(a) 16
(b) 14
(c) – 4
(d) – 5
Answer
C
Question. Let p(x) be a quadratic polynomial such that p(0)=1. If p(x) leaves remainder 4 when divided by x–1 and it leaves remainder 6 when divided by x+1; then :
(a) p(b) = 11
(b) p(b) = 19
(c) p(–2) = 19
(d) p(–2) = 11
Answer
C
Question. In a triangle PQR, ∠R = π/2. If tan (p/2) and – tan (Q/2) are the roots of ax2 + bx + c = 0, a ≠ 0 then
(a) a = b + c
(b) c = a + b
(c) b = c
(d) b = a + c
Answer
B
Question. If the roots of the equation x2 – bx + c = 0 be two consecutive integers, then b2 – 4c equals
(a) – 2
(b) 3
(c) 2
(d) 1
Answer
D
Question. The sum of all real values of x satisfying the equation (x2 – 5x + 5)x2+4x-60 = 1 is :
(a) 6
(b) 5
(c) 3
(d) – 4
Answer
C