See below CBSE Class 12 Mathematics Sample Paper Set A with solutions. We have provided CBSE Sample Papers for Class 12 Mathematics as per the latest paper pattern issued by CBSE for the current academic year. All sample papers provided by our Class 12 Mathematics teachers are with answers. You can see the sample paper given below and use them for more practice for Class 12 Mathematics examination.
PART – A
Section – I
1. Solve the differential equation dy/dx = 1-x+y+-xy.
Answer :
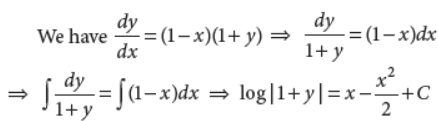
What is the degree of the differential equation
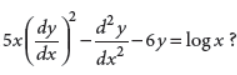
Answer : Since greatest power of highest order derivative is 1, therefore degree of the given differential equation is 1.
2. If
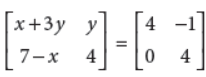
then find the values of x and y.
Answer :
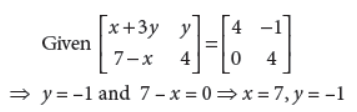
3. The random variable X has a probability distribution P(X) of the following form, where ‘k’ is some number,
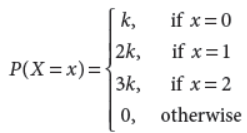
Determine the value of ‘k’.
Answer :
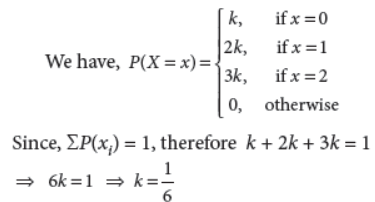
OR
Out of 8 outstanding students of a school, in which there are 3 boys and 5 girls, a team of 4 students is to be selected for a quiz competition. Find the probability that 2 boys and 2 girls are selected.
Answer : Total number of students = 8
The number of ways to select 4 students out of 8 students

4. Check whether the relation R on the set A = {1, 2, 3} defined as R = {(1, 1), (1, 2), (2, 1), (3, 3)} is reflexive, symmetric and transitive.
Answer : Given, R = {(1, 1), (1, 2), (2, 1), (3, 3)}
Since, (2, 2) ∉ R
Therefore, R is not reflexive.
But R is both symmetric and transitive as (1, 2) ∈ R
⇒ (2, 1) ∈ R and (1, 1) ∈ R, (2, 1) ∈ R ⇒ (1, 1) ∈ R.
5. Evaluate :
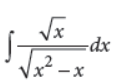
Answer :
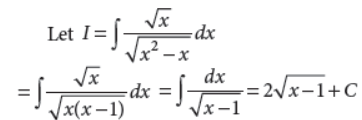
OR
Evaluate :
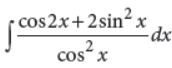
Answer :
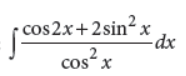
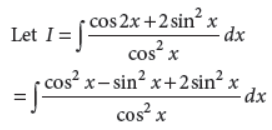
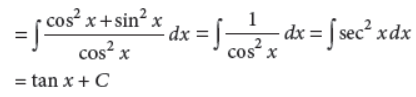
6. If lines
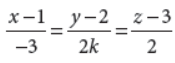
and
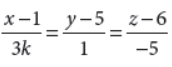
are mutually perpendicular, then find the value of k.
Answer :
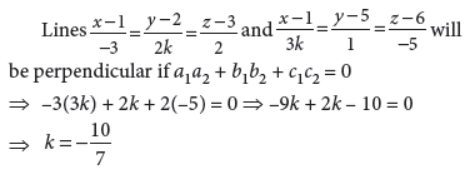
7. Find the vector equation of a plane which is at a distance of 6 units from the origin and which has k̂ as the unit vector normal to it.
Answer :
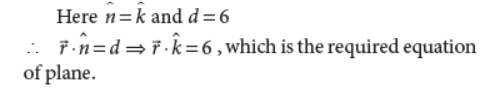
OR
Find the vector equation of the plane which is at a distance of 6/√29 units from the origin and its normal vector from the origin is 2î – 3ĵ + 4k̂.
Answer :
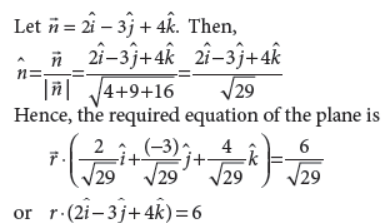
8. Prove that for any square matrix A, AAT is a symmetric matrix.
Answer : Clearly, (AAT)T = (AT)T ⋅ AT [ (AB)T = BTAT]
⇒ (AAT)T = AAT [ (XT)T = X]
⇒ AAT is a symmetric matrix.
9. If
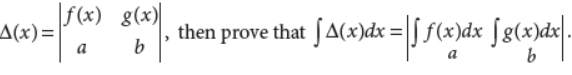
Answer :
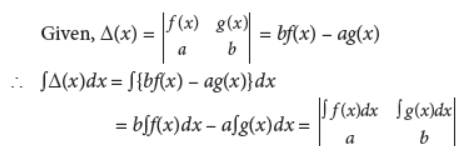
OR
If A is invertible matrix of order 3 × 3, then prove that |A–1| = |A|–1.
Answer : Given, A is a matrix of order 3 × 3, then

10. Two dice are thrown together. What is the probability that the sum of the numbers on the two faces is neither 9 nor 11 ?
Answer : If two dice are thrown, then total number of cases = 36
Cases for total of 9 or 11 are {(3, 6), (4, 5), (6, 3), (5, 4), (6, 5), (5, 6)}, i.e., 6 in number.
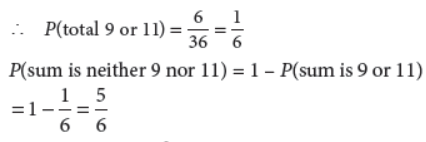
11. Let f : [2, ∞) → R be the function defined by f (x) = x2 – 4x + 5, then find the range of f.
Answer : Given, f(x) = x2 – 4x + 5
Let y = x2 – 4x + 5 ⇒ y = (x – 2)2 + 1
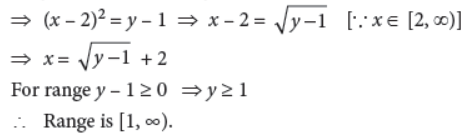
12. If A and B are two events such that P(A) = 0.2 , P(B) = 0.4 and P(A ∪ B) = 0.5 , then find the value of P(A/B).
Answer : We have, P(A) = 0.2, P(B) = 0.4 and P(A ∪ B) = 0.5
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 0.2 + 0.4 – 0.5 = 0.1
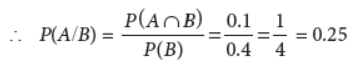
13. Evaluate :
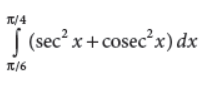
Answer :
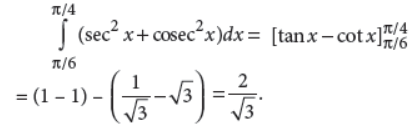
14. A bag contains 3 white and 6 black balls while another bag contains 6 white and 3 black balls. A bag is selected at random and a ball is drawn. Find the probability that the ball drawn is of white colour.
Answer : Let E1 be the event that bag I is selected
E2 be the event that bag II is selected
E be the event that the ball drawn is of white colour.
By rule of total probability,
P(E) = P(E1)·P(E|E1) + P(E2)·P(E|E2)
1/2.3/9 +1/2.6/9 = 9/18 = 1/2
15. If ā , Ђ ,ċ, , are the position vectors of points A, B, C respectively such that 5ā –3Ђ – 2ċ = 0 , then find the ratio in which C divides AB externally.
Answer : Given, 5a̅ – 3b̅ – 2c̅ = ô ⇒ 2c̅ = 5a̅ – 3b̅
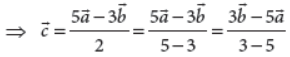
So, C divides AB externally in the ratio 3 : 5
16. For real numbers x and y, we write xRy ⇔ x − y +√2 is an irrational number. Prove that the relation R is not transitive.
Answer : Clearly, √2R1 and 1R2√2 but √2 R 2√2 ,therefore R is not transitive.
Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. A building of a multinational company is to be constructed in the form of a triangular pyramid, ABCD as shown in the figure.

Let its angular points are A(3, 0, 1), B(–1, 4, 1), C(5, 2, 3) and D(0, –5, 4) and G be the point of intersection of the medians of DBCD.
Based on the above answer the following.
(i) The coordinates of points G are
(a) (1/3 , 1/3 ,1/3)
(b) (0, 1/2 ,1/3)
(c) (4/3 , 1/3 ,8/3)
(d) (4/3 , 8/3 ,1/3)
Answer : C
(ii) The length of vector AG is
(a) √17 units
(b) √51/3 units
(c) 3/√6 units
(d) √59/4 units
Answer : B
(iii) Area of triangle ABC (in sq. units) is
(a) 24
(b) 8√6
(c) 4√6
(d) 5√6
Answer : C
(iv) The sum of lengths of AB ACand is
(a) 4 units
(b) 9.1 units
(c) 8.7 units
(d) 6 units
Answer : B
(v) The length of the perpendicular from the vertex D on the opposite face is
(a) 14/√6 units
(b) 2/√6 units
(c) 3/√6 units
(d) 8√6 units
Answer : A
18. A concert is organised every year in the stadium that can hold 42000 spectators. With ticket price of 10, the average attendance has been 27000. Some financial expert estimated that price of a ticket should be determined by the function p(x) =19–x/3000, where x is the number of tickets sold.
Based on the above information, answer the following questions.

(i) The revenue, R as a function of x can be represented as
(a) 19x–x2/3000
(b) 19–x2/3000
(c) 19x–1/3000
(d) 19x–x/3000
Answer : A
(ii) The range of x is
(a) [27000, 42000]
(b) [0, 27000]
(c) [0, 42000]
(d) none of these
Answer : C
(iii) The value of x for which revenue is maximum, is
(a) 20000
(b) 27000
(c) 28500
(d) 28000
Answer : C
(iv) When the revenue is maximum, the price of the ticket is
(a) ₹8
(b) ₹5
(c) ₹9
(d) ₹9.5
Answer : D
(v) How many spectators should be present to maximize the revenue?
(a) 25000
(b) 27000
(c) 22000
(d) 28500
Answer : D
PART – B
19. Solve the differential equation dy/dx = ex-y + x2e-y .
Answer :
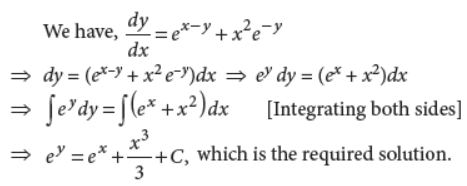
20. Find the area of the larger part bounded by y = cos x, y = x + 1 and y = 0.
Answer : It can be observed that y = cos x and y = x + 1 meet at the point (0, 1).
Also, y = x + 1 passes through the points (–1, 0) and (0, 1),

OR
Find the area enclosed by the lines y = 0, y = x, x = 1, x = 2.
Answer : Given lines are y = x, x = 1, x = 2 and y = 0.
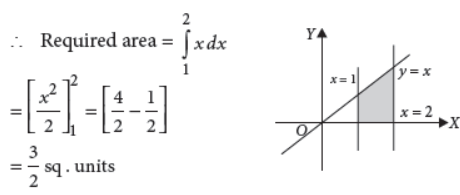
21. Consider f(x)
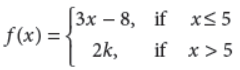
Find the value of k, if f(x) is continuous at x = 5.
Answer : We have, L.H.L. (at x = 5)
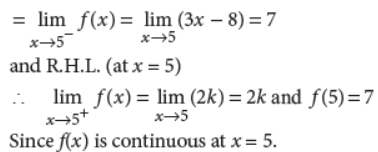
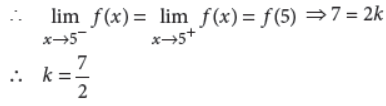
22. A random variable X has the following distribution.

For the event E = {X is prime number} and F = {X < 4}, find P(E ∪ F).
Answer : Clearly, P(E) = P(X = 2) + P(X = 3) + P(X = 5) + P(X = 7)
= 0.23 + 0.12 + 0.20 + 0.07 = 0.62
P(F) = P(X = 1) + P(X = 2) + P(X = 3)
= 0.15 + 0.23 + 0.12 = 0.50
P (E ∩ F) = P(X = 2) + P(X = 3) = 0.23 + 0.12 = 0.35
∴ P(E ∪ F) = P(E) + P (F) – P (E ∩ F)
= 0.62 + 0.50 – 0.35 = 0.77.
23. Find the direction cosines of the line passing through the two points (–2, 4, –5) and (1, 2, 3).
Answer : We know that the direction cosines of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by

OR
If O be the origin and the coordinates of P be (1, 2, – 3), then find the equation of the plane passing through P and perpendicular to OP.
Answer : The direction ratios of OP are < 1 – 0, 2 – 0, – 3 – 0 > i.e.
<1, 2, –3 >
∴ The equation of the plane passing through P and perpendicular to OP is
(1) (x – 1) + (2) (y – 2) + (– 3) (z + 3) = 0
⇒ x – 1 + 2y – 4 – 3z – 9 = 0
⇒ x + 2y – 3z – 14 = 0
24. Find cofactors of a21 and a31 of the matrix.
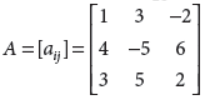
Answer : Let Mij and Cij respectively denote the minor and cofactor of element aij in A. Then,
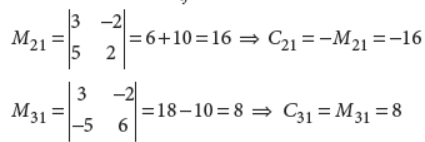
25. Evaluate :
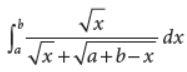
Answer :
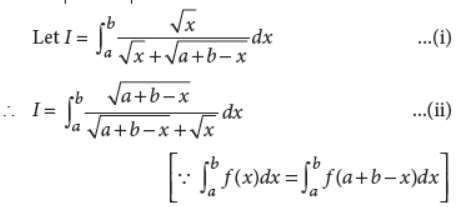
On adding (i) and (ii), we get
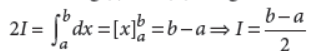
26. Let k and K be the minimum and the maximum values of the function, f(x) = (1+x)0,6/1+x0,6 defined on [0, 1], respectively. Find the ordered pair (k, K).
Answer :
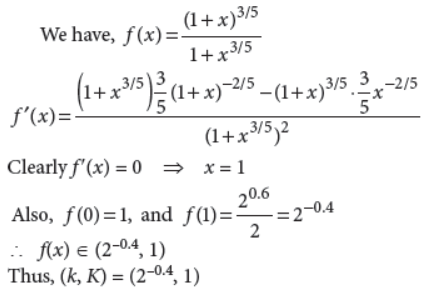
27. Find the number of triplets (x, y, z) satisfying the equation sin–1x + sin–1y + sin–1z = 3Π/2.
Answer :
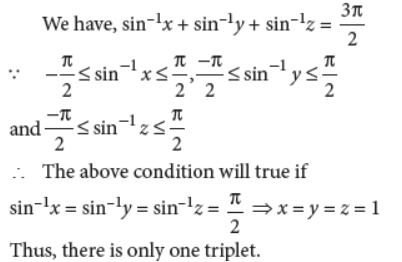
28. Given that the events A and B are such that P(A) = 1/2 ,P(A∪B) = 3/5 and P(B) = p. Find p if A and B are (i) mutually exclusive (ii) independent.
Answer : (i) When A and B are mutually exclusive, then A ∩ B = f ⇒ P(A ∩ B) = 0 ⇒ P(A ∪ B) = P(A) + P(B)
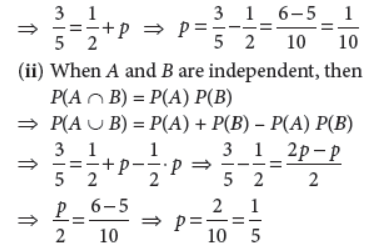
OR
A bag contains 12 white pearls and 18 black pearls. Two pearls are drawn in succession without replacement.
Find the probability that the first pearl is white and the second is black.
Answer : Let A and B be the events of getting a white pearl in the first draw and a black pearl in the second draw respectively.
Now, P(A) = P(getting a white pearl in the first draw) = 12/30 = 2/5
When second pearl is drawn without replacement, the probability that the second pearl is black is the conditional probability of the event B occurring when A has already occurred.
∴ P(B|A) = 18/29
By multiplication rule of probability, we have
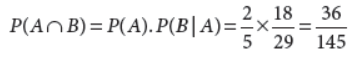
Section – IV
29. Find all points of discontinuity of f, where f is defined as follows :
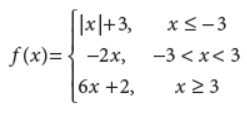
Answer :

30. Solve the differential equation
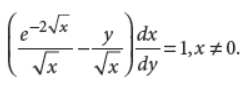
Answer :

31. If y = (logcosxsinx)(logsinx cosx)–1 + sin–1 (2x/1+x2) find dy/dx at x =Π/4.
Answer :
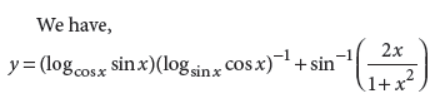

OR
If x = 2 cos q – cos2q and y = 2 sin q – sin2q, find d2y/dx2 at θ = Π/2.
Answer : We have, x = 2 cosθ – cos2θ and y = 2sinθ – sin2θ

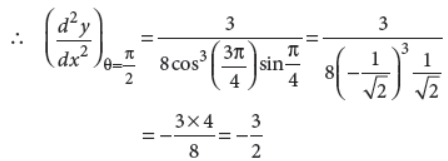
32. Find the area of the smaller region bounded by the ellipse x2/9 + y2/4 = 1 and the line x/3 + y/2 = 1.
Answer :
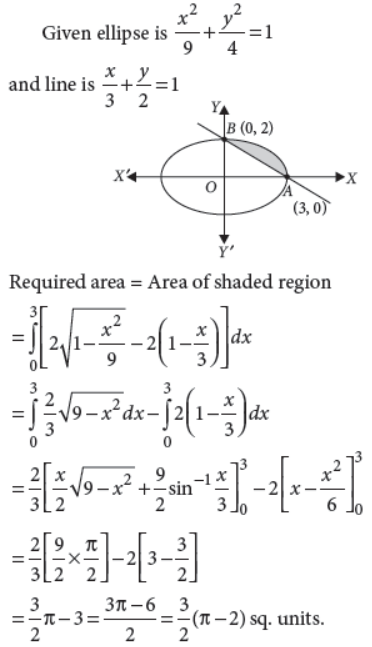
33. Let A and B be non-empty sets. Show that f : A × B → B × A such that f (a, b) = (b, a) is a bijective function.
Answer : Injectivity : Let (a1, b1) and (a2, b2) ∈ A × B such that, f(a1, b1) = f(a2, b2)
⇒ (b1, a1) = (b2, a2) ⇒ b1= b2and a1 = a2
⇒ (a1, b1) = (a2, b2)
Thus, f(a1, b1) = f(a2, b2) ⇒ (a1, b1) = (a2, b2)
for all (a1, b1), (a2, b2) ∈ A × B.
So, f is an injective function.
Surjectivity : Let (b, a) be an arbitrary element of
B × A, where, b ∈ B and a ∈ A ⇒ (a, b) ∈ A × B
Thus, for all (b, a) ∈ B × A, their exists (a, b) ∈ (A × B)
such that, f (a, b) = (b, a)
So, f : A × B → B × A is an onto function.
Hence, f is a bijective function.
34. If f(x) = a log |x| + bx2 + x has extreme values at x = – 1 and at x = 2, then find a and b.
Answer :
Clearly, domain (f ) = R – {0}
We have, f(x) = a log |x| + bx2 + x
⇒ f ′(x) = a/x + 2bx + 1
Since f(x) has extreme values at x = –1 and x = 2.
Therefore, f ′(–1) = 0 and f ′(2) = 0
⇒ –a – 2b + 1 = 0 and a/2 + 4b+1 = 0
⇒ a + 2b = 1 …(i)
and a + 8b = –2 …(ii)
Solving (i) and (ii), we get
a = 2 and b = −1/2
OR
Show that f(x) = cos (2x + Π/4) is an increasing function on (3Π/8, 7Π/8).
Answer : We have, f(x) = cos(2x + π/4)
⇒ f ′(x) = –2 sin (2x + π/4)
Now, x ∈ (3π/8, 7π/8)
⇒ 3π/8 < x < 7π/8 ⇒ 3π/4 < 2x < 7π/4 ⇒ π/4 + 3π/4 < 2x + π/4 < 7π/4 + π/4 ⇒ π < 2x + π/4 < 2π ⇒ sin (2x + π/4) < 0 [ sine function is negative in third and fourth quadrants] ⇒ –2 sin (2x + π/4) > 0 ⇒ f ′(x) > 0
Hence, f(x) is increasing on (3π/8, 7π/8).
35. Evaluate :
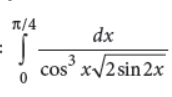
Answer :
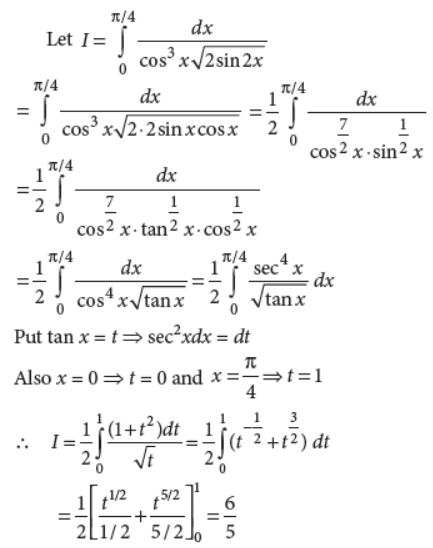
Section – V
36. Find the cartesian equations of the plane through the intersection of the planes r̄.(2î+6ĵ) + 24 = 0 and r̄.(3î–ĵ+4k̂) which are at a distance of 2 units from the origin.
Answer : Any plane through the line of intersection of the planes
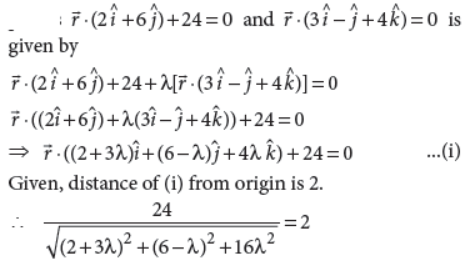
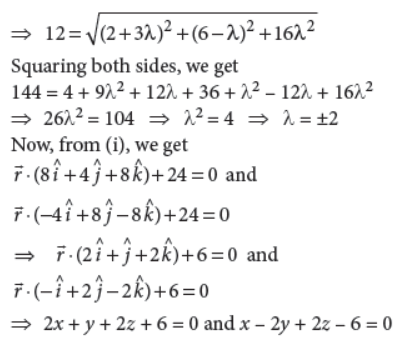
OR
If the shortest distance between the lines
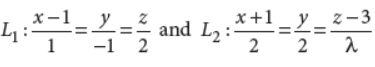
is unity, then find the value of λ.
Answer : The lines are x–1 = y/-1 = z/2 …(i)
and x+1/2 = y/2 = z–3/λ …(ii)
Here, x1 = 1, y1 = 0, z1 = 0
a1 = 1, b1 = –1, c1 = 2
x2 = –1, y2 = 0, z2 = 3
a2 = 2, b2 = 2, c2 = l

37. Solve the following LPP graphically.
Maximize Z = 50x + 40y
Subject to constraints :
1000x + 1200y ≤ 7600
12x + 8y ≤ 72
x, y ≥ 0
Answer : The given problem can be written as
Maximize Z = 50x + 40y
subject to constraints :
5x + 6y ≤ 38
3x + 2y ≤ 18
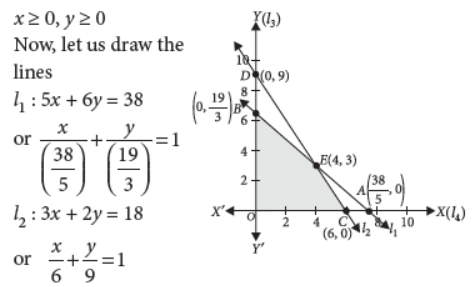
Lines l1 and l2 intersect at E(4, 3).
The shaded region OCEB is the feasible region which is bounded.
Corner points of the feasible region are O(0, 0), C(6, 0),E(4, 3) and B (0,19/3)
The value of the objective function Z = 50x + 40y at corner points are given below:
At O, Z = 50 × 0 + 40 × 0 = 0
At C, Z = 50 × 6 + 40 × 0 = 300
At E, Z = 50 × 4 + 40 × 3 = 320 (Maximum)
At B, Z = 50 × 0 + 40 × 19/3 = 253.33
Clearly, the maximum value is 320 at E(4, 3).
OR
Solve the following LPP graphically.
Minimize Z = 5x + 7y
Subject to constraints :
2x + y ≤ 8
x + 2y ≥ 10
and x, y ≥ 0
Answer : The given problem is
Minimize Z = 5x + 7y
subject to 2x + y ≤ 8
x + 2y ≥ 10 and x, y ≥ 0
To solve this LPP graphically, we first convert the
inequations into equations to obtain the following line
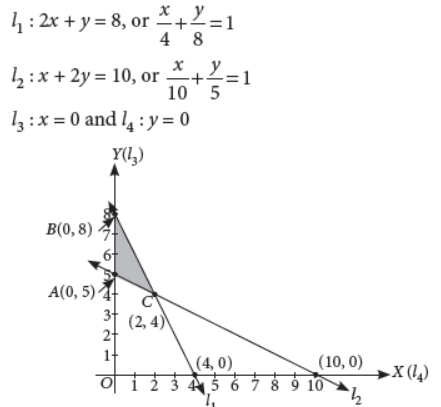
The coordinates of the corner points of the feasible region ABC are A(0, 5), B(0, 8) and C(2, 4). The values of the objective function Z = 5x + 7y at the corner points of the feasible region are given in the following table.
| Corner Points | Value of Z = 5x + 7y |
| A(0, 5) | 5 × 0 + 7 × 5 = 35 (Minimum) |
| B(0, 8) | 5 × 0 + 7 × 8 = 56 |
| C(2, 4) | 5 × 2 + 7 × 4 = 38 |
Thus, Z is minimum when x = 0 and y = 5.
38. If
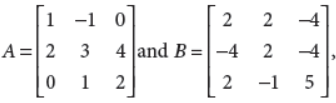
then find AB. Hence, solve the system of equations :
x – y = 6, 2x + 3y + 4z = 34, y + 2z = 14
Answer :

The given system of equations is
x – y + 0z = 6
2x + 3y + 4z = 34
0x + y + 2z = 14
This system of equations can be written as
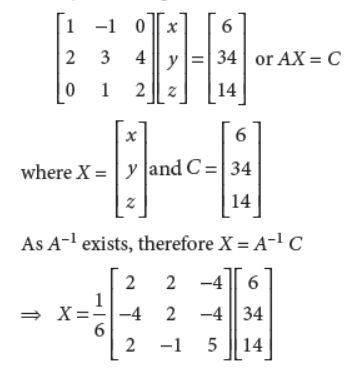
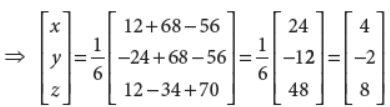
⇒ x = 4, y = – 2, z = 8
Hence, the solution of the given system of equations is
x = 4, y = – 2, z = 8.
OR
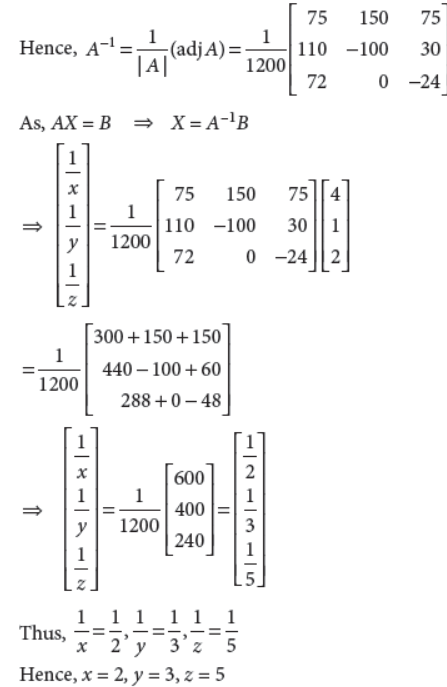
Solve the system of the following equations :
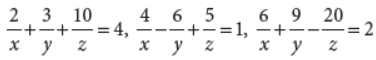
Answer : The equations can be written in the form AX = B,