Case Study Chapter 2 Polynomials Mathematics

Please refer to Case Study Chapter 2 Polynomials Mathematics with answers provided below. These case study based questions are expected to come in the upcoming Class 10 Mathematics examinations. We have provided case study questions class 10 maths for all chapters on our website as per the latest examination pattern issued by CBSE, NCERT, and KVS.

Chapter 2 Polynomials Case study Questions Class 10 Maths

I. A highway underpass is parabolic in shape.Parabola: A parabola is the graph that results from p(x) = ax² + bx + c. Parabolas are symmetric about a vertical line known as the Axis of Symmetry. The Axis of Symmetry runs through the maximum or minimum point of the parabola which is called the vertex.   

Question. Graph of a quadratic polynomial is a     
(a) straight line
(b) circle
(c) parabola
(d) ellipse

Question. If the highway overpass is represented by x² – 2x – 8, then its zeroes are   
(a) (2, –4)
(b) (4, –2)
(c) (–2, –2)
(d) (–4, –4)

Question. The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is     
(a) x² – 6x + 2
(b) x² – 36
(c) x² – 6
(d) x² – 3

Question. The number of zeroes that polynomial f (x) = (x – 2)² + 4 can have is:     
(a) 1
(b) 2
(c) 0
(d) 3

Question. The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomial     
(a) intersects x-axis
(b) intersects y-axis
(c) intersects y-axis or x-axis
(d) None of these

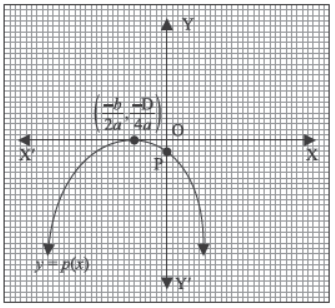
II. Due to heavy storm an electric wire got bent as shown in the figure. It followed a mathematical shape. Answer the following questions below:

Question. The zeroes of the polynomial are   
(a) –1, 5
(b) –1, 3
(c) 3, 5
(d) –4, 2

Question. How many zeroes are there for the polynomial (shape of the wire)?   
(a) 2
(b) 3
(c) 1
(d) 0

Question. What is the value of the polynomial if x = –1 ?   
(a) 6
(b) –18
(c) 18
(d) 0

Question. What will be the expression of the polynomial ?   
(a) x² + 2x – 3
(b) x² – 2x + 3
(c) x² – 2x – 3
(d) x² + 2x + 3

Question. Name the shape in which the wire is bent.   
(a) spiral
(b) ellipse
(c) linear
(d) parabola

III. An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe the poses that can be related to represent of a quadratic polynomial.

Question. In the graph, how many zeroes are there for the polynomial ?    

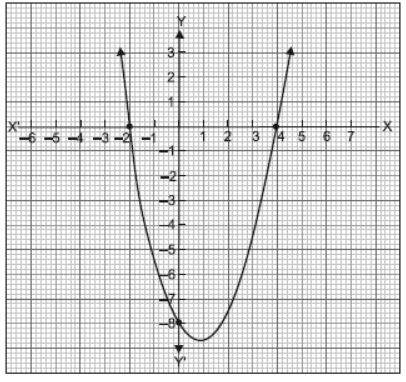
(a) 0
(b) 1
(c) 2
(d) 2

Question. The two zeroes in the above shown graph are   
(a) 2, 4
(b) –2, 4
(c) –8, 4
(d) 2, –8

Question. The shape of the poses shown is   
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola

Question. The zeroes of the quadratic polynomial 4 √3x² + 5x − 2 √3  are     
(a) 2 /√3 , √3/ 4
(b) − 2/√3 , √3/4 
(c) 2 /√3 , √3/4
(d) −2/ √3, −√3/ 4

Question. The graph of parabola opens downwards, if _______   
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0

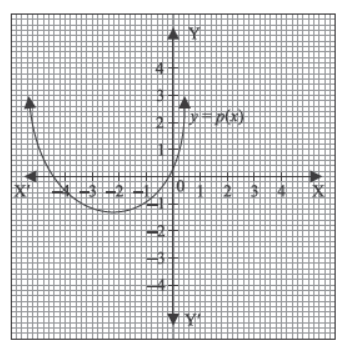
IV. Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

Question. Observe the following graph and answer 

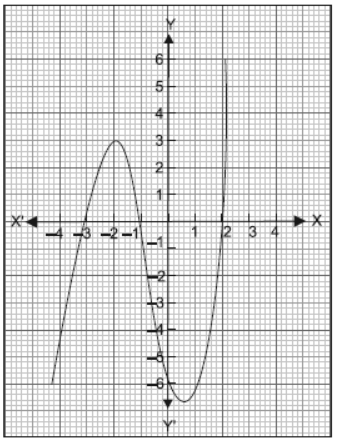
In the above graph, how many zeroes are there for the polynomial?   
(a) 0
(b) 1
(c) 2
(d) 3

Question. What will be the expression of the polynomial ?     
(a) x³ + 2x² – 5x – 6
(b) x³ + 2x² – 5x + 6
(c) x³ + 2x² + 5x – 6
(d) x³ + 2x² + 5x + 6

Question. The shape of the path traced shown is   
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola

Question. The three zeroes in the above shown graph are     
(a) 2, 3, –1
(b) –2, 3, 1
(c) –3, –1, 2
(d) –2, –3, –1

Question. The graph of parabola opens upwards, if _______   
(a) a = 0
(b) a < 0
(c) a > 0
(d) a ≥ 0

I. Skipping Rope 
Skipping rope is a good exercise. It burns calories, makes bones strong and improves heart health. During skipping, when rope goes up and down it makes the shape of parabolas (graphs of quadratic polynomials). Observe the following skipping pictures.

Question. If 1/ 4 and –1 are the sum and product of zeroes of a polynomial whose graph is represented by Picture (3), the quadratic polynomial is   
(a) k (x² − 1/4 x − 1)  
(b) k (1/4 x² − x − 1)
(c) k (x² + 1/ 4 x + 1) 
(d) k (1/ 4 x² + x +1)

Question. Let the Picture (1) represents the quadratic polynomial f (x) = x² – 8x + k whose sum of the squares of zeroes is 40. The value of k is   
(a) 8
(b) 10
(c) 12
(d) 20

Question. The graph of polynomial p(x) represented by Picture 2 is shown below. Which of the following has negative (–) sign?   

(a) a
(b) b
(c) c
(d) All of these.

Question. Let the Picture (3) represents the quadratic polynomial f (x) = x² + 7x + 10. Then its zeroes are   
(a) –1, –5
(b) –2, –5
(c) 1, 5
(d) 2, 5

Question. The graph of polynomial p(x) represented by Picture 1 is shown below. The number of zeroes of the polynomial is      

(a) 0
(b) 1
(c) 2
(d) 4

II. Rainbow is an arch of colours that is visible in the sky, caused by the refraction and dispersion of the sun’s light after rain or other water droplets in the atmosphere. The colours of the rainbow are generally said to be red, orange, yellow, green, blue, indigo and violet. Each colour of rainbow makes a parabola. We know that for any quadratic polynomial ax² + bx + c, a ≠ 0, the graph of the corresponding equation y = ax² + bx + c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas.

Question. The graph of a rainbow y = f (x) is shown below. The number of zeroes of f (x) is     

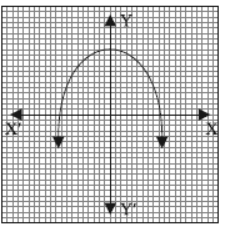
(a) 0
(b) 1
(c) 2
(d) 3

Question. A rainbow is represented by the quadratic polynomial x² + (a + 1)x + b whose zeroes are 2 and –3. Then   
(a) a = –7, b = –1
(b) a = 5, b = –1
(c) a = 2, b = –6
(d) a = 0, b = –6

Question. If graph of a rainbow does not intersect the x-axis but intersects y-axis in one point, then number of zeroes of the polynomial is equal to   
(a) 0
(b) 1
(c) 0 or 1
(d) none of these

Question. The representation of a rainbow is a quadratic polynomial. The sum and the product of its zeroes are 3 and –2 respectively. The polynomial is   
(a) k(x² – 2x – 3), for some real k.
(b) k(x² – 5x – 9), for some real k.
(c) k(x² – 3x – 2), for some real k.
(d) k(x² – 8x + 2), for some real k.

Question. The polynomial x² – 2x – (7p + 3) represents a rainbow. If –4 is zero of it, then the value of p is   
(a) 1
(b) 2
(c) 3
(d) 4

III. The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

Question. If α and 1/ α are the zeroes of the quadratic polynomial 2x² – x + 8k, then k is     
(a) 4
(b) 1/ 4
(c) −1/ 4
(d) 2

Question. The graph of x² + 1 = 0     
(a) Intersects x-axis at two distinct points
(b) Touches x-axis at a point
(c) Neither touches nor intersects x-axis
(d) Either touches or intersects x-axis

Question. In the standard form of quadratic polynomial, ax² + bx + c; a, b and c are   
(a) All are real numbers.
(b) All are rational numbers.
(c) ‘a’ is a non-zero real number and b and c are any real numbers.
(d) All are integers.

Question. If the sum of the roots is –p and product of the roots is – 1/ p , then the quadratic polynomial is     
(a) k (−px² + x/p +1)
(b) k (px² −x/p − 1)  
(c) k (x²+ px − 1/p)
(d) k (x² − px + 1/p)

Question. If the roots of the quadratic polynomial are equal, where the discriminant D = b² – 4ac, then   
(a) D > 0
(b) D < 0
(c) D ≥ 0
(d) D = 0

We hope you liked the above provided Case Study Chapter 2 Polynomials Mathematics case study questions class 10 maths provided above. Please let us know in the comments box below if you have any questions.