Assignments Class 12 Physics Nuclei

Please refer to Assignments Class 12 Physics Nuclei Chapter 13 with solved questions and answers. We have provided Class 12 Physics Assignments for all chapters on our website. These problems and solutions for Chapter 13 Nuclei Class 12 Physics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.

Nuclei Assignments Class 12 Physics

Question: The equation 4¹₁H⁺→ ⁴₂He²⁺+2e^–+26 MeV represents 
(a) both fusion and fission
(b) neither fusion nor fission
(c) only fusion
(d) only fission 

Question: In nuclear reaction, there is conservation of
(a) mass only
(b) energy only
(c) momentum only
(d) mass, energy and momentum 

Question: The fission properties of 239₉₄  Pu are very similar to those of 235₉₂U. The average energy released per fission is 180 MeV. If all the atoms in 1 kg of pure 239₉₄Pu undergo fission, then the total energy released in MeV is
(a) 4.53 × 10²⁶ MeV
(b) 2.21 × 10¹⁴ MeV
(c) 1 × 10¹³ MeV
(d) 6.33 × 10²⁴ MeV 

Question: If 200 MeV energy is released in the fission of a single nucleus of ²³⁵₉₂U, the fissions which are required to produce a power of 1 kW is
(a) 3.125 × 10¹³
(b) 1.52 × 10⁶
(c) 3.125 × 10¹²
(d) 3.125 × 10¹⁴   

Question: In nuclear reactors, the control rods are made of
(a) cadmium
(b) graphite
(c) krypton
(d) plutonium   

Question: The ratio of the nuclear radii of the gold isotope  ¹⁹⁷₇₉Au and silver isotope ¹⁰⁷₄₇Ag is 
(a) 1.23
(b) 0.216
(c) 2.13
(d) 3.46 

Question: The equivalent energy of 1 g of substance is
(a) 9 × 10¹³ J
(b) 6 × 10¹² J
(c) 3 × 10¹³ J
(d) 6 × 10¹³ J 

Question: The mass number of iron nucleus is 55.854 and A = 56, the nuclear density is
(a) 2.29 × 10¹⁶ kg m^–3
(b) 2.29 × 10¹⁷ kg m^–3
(c) 2.29 × 10¹⁸ kg m^–3
(d) 2.29 × 10¹⁵ kg m^–3

Question: Order of magnitude of density of uranium nucleus is
(a) 10²⁰ kg m^–3
(b) 10¹⁷ kg m^–3
(c) 10¹⁴ kg m^–3
(d) 10¹¹ kgm^–3 

Question: How much mass has to be converted into energy to produce electric power of 500 MW for one hour?
(a) 2 × 10^–5 kg
(b) 1 × 10^–5 kg
(c) 3 × 10^–5 kg
(d) 4 × 10^–5 kg 

Case Based MCQs

Nuclear Fission
In the year 1939, German scientist Otto Hahn and Strassmann discovered that when anuranium isotope was bombarded with a neutron, it breaks into two intermediate mass fragments.
It was observed that, the sum of the masses of new fragments formed were less than the mass of the original nuclei. This difference in the mass appeared as the energy released in the process.
Thus, the phenomenon of splitting of a heavy nucleus (usually A > 230) into two or more lighter nuclei by the bombardment of proton, neutron,a-particle, etc with liberation of energy is called nuclear fission.
92U²³⁵ + 0n¹ → 92U²³⁶ → 56Ba¹⁴⁴ + 36Kr⁸⁹
Unstable nucleus
                                              + 30n¹ + Q
Question: For sustaining the nuclear fission chain reaction in a sample (of small size) of 235₉₂U, it is desirable to slow down fast neutrons by
(a) friction
(b) elastic damping/scattering
(c) absorption
(d) cooling 

Question: Which of the following is/are fission reaction(s)?
(a) Both II and III
(b) Both I and III
(c) Only II
(d) Both I and II 

Question: Nuclear fission can be explained on the basis of
(a) Millikan’s oil drop method
(b) Liquid drop model
(c) Shell model
(d) Bohr’s model. 

Question: In any fission process, ratio of mass of daughter nucleus to mass of parent nucleus is
(a) less than 1
(b) greater than 1
(c) equal to 1
(d) depends on the mass of parent nucleus. 

Question: On an average, the number of neutrons and the energy of a neutron released per fission of a uranium atom are respectively
(a) 2.5 and 2 keV
(b) 3 and 1 keV
(c) 2.5 and 2 MeV
(d) 2 and 2 keV   

Nuclear Force
 Neutrons and protons are identical particle in the sense that their masses are nearly the same and the force, called nuclear force, does into distinguish them. Nuclear force is the strongest force. Stability of nucleus is determined by the neutron proton ratio or mass defect or packing fraction. Shape of nucleus is calculated by quadrupole moment and spin of nucleus depends on even or odd mass number. Volume of nucleus depends on the mass number. Whole mass of the atom (nearly 99%) is centred at the nucleus.

Question: The range of nuclear force is the order of
(a) 2 × 10–10 m
(b) 1.5 × 10–20 m
(c) 1.2 × 10–4 m
(d) 1.4 × 10–15 m 

Question: The correct statements about the nuclear force is/are
(a) charge independent
(b) short range force
(c) non-conservative force
(d) all of these. 

Question: A force between two protons is same as the force between proton and neutron. The nature of the force is
(a) electrical force
(b) weak nuclear force
(c) gravitational force
(d) strong nuclear force.   

Question: All the nucleons in an atom are held by
(a) nuclear forces
(b) Van der Waal’s forces
(c) tensor forces
(d) coulomb forces 

Question: Two protons are kept at a separation of 40 Å.
Fn is the nuclear force and Fe is the electrostatic force between them. Then
(a) Fn << Fe
(b) Fn = Fe
(c) Fn >> Fe
(d) Fn ≈ Fe   

Assertion & Reasoning Based MCQs
Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false

Question: Assertion (A) : Density of all the nuclei is same.
Reason (R) : Radius of nucleus is directly proportional to the cube root of mass number. 

Question: Assertion (A) : A fission reaction can be more easily controlled than a fusion reaction.
Reason (R) : The percentage of mass converted to energy in a fission reaction is 0.1% whereas in a fusion reaction it is 0.4%. 

Question: Assertion (A) : Cadmium rods used in a nuclear reactor, control the rate of fission.
Reason (R) : Cadmium rods speed up the slow neutrons. 

Question: Assertion (A) : Thermonuclear fusion reactions may become the source of unlimited power for the mankind.
Reason (R) : A single fusion event involving isotopes of hydrogen produces more energy than energy from nuclear fission of a single uranium.

Very Short Answer Type Questions 

Question: The nuclear radius of a nucleus with nucleon number 16 is 3 × 10^–15 m. Then, find the nuclear radius of a nucleus with nucleon number 128?
Answer: Radius R of a nucleus changes with the nucleon number A of the nucleus as

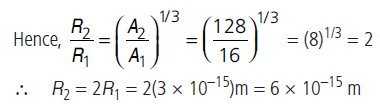
Question: The three stable isotopes of neon : ²⁰₁₀Ne ,²¹₁₀Ne and ²²₁₀
Ne have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
Answer:  Average atomic mass of neon with the given abundances,
A = 90.51 (19.99u)+ 0.27 (20. 99u) +9.22(21. 99u)/100
A= = 2017. 7/100 u = 20.18u

Question: From the relation R = R0 A^1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A).
Answer: Density of nuclear matter = Mass of nucleus/Volume

As R₀ is constant, r is constant
So, nuclear density is constant irrespective of mass number or size.

Short Answer Type Questions 

Question: A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z₁ = N₂ and Z₂ = N₁. (a) Which nuclide is a mirror isobar of ²³₁₁Na ?
(b) Which nuclide out of the two mirror isobars have greater binding energy and why?
Answer:

Question: Calculate for how many years will the fusion of 2.0 kg deuterium keep 800 W electric lamp glowing. Take the fusion reaction as
²₁H + ²₁H → ³₂He + ¹₀n + 3.27 MeV
Answer: Given m = 2 kg, P = 800 W.
Here two deuterium nuclei produce 3.27 MeV energy

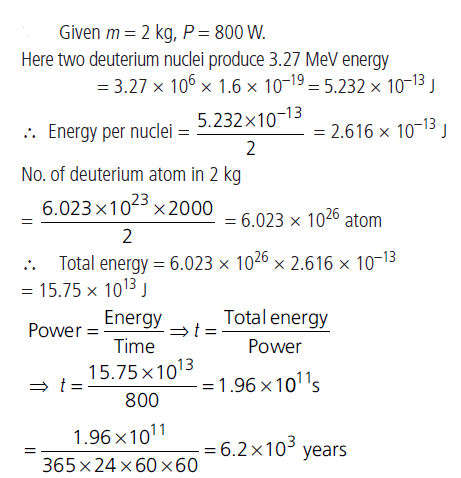
Question: Consider a particle or nucleus, which contains 2 protons and 2 neutrons. Find its binding energy.
m_p = 1.007276 u, m_n = 1.008665 u
m_He = 4.001508 u
Answer:  B.E. = (2m_p + 2m_n – m_He)u × 931 MeV
= [2(1.007276 u + 1.008665 u) – 4.001508 u] × 931 MeV
= [4.031882 u – 4.001508 u] × 931 MeV
= 0.030374 × 931 MeV
B.E. = 28.3 MeV

Question: Consider the fusion reaction:
⁴He + ⁴He → ⁸Be
For the reaction, find (i) mass defect (ii) Q-value
(iii) Is such a fusion energetically favourable?
Atomic mass of ⁸Be is 8.0053 u and that of ⁴He is 4.0026 u.
Answer: ⁴He + ⁴He → ⁸Be + Q
(i) Dm = 2 × 4.0026 – 8.0053 = 8.0052 – 8.0053
= – 0.0001 amu
(ii) Q = (2m_He – m_Be) c²
= (2 × 4.0026 – 8.0053)c² × 931MeV/c²
= –0.0931 MeV = –93.1 keV
(iii) Since Q is negative, the fusion is not energetically favourable.

Question: Why do stable nuclei never have more protons than neutrons?
Answer: The stability of a nucleus depends on its neutron to proton ratio. More is the number of protons in the nucleus, greater is the electrical forces between them. Therefore more neutrons are needed to provide the strong attractive force necessary to keep the nucleus stable.

Question: The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge e′: image 20 Estimate the value of (e′/e) given that the binding energy of a deuteron is 2.2 MeV.
Answer: We know that binding energy of hydrogen atom in ground state, 

Questions A nuclear reactor using ²³⁵U generates 250 MW of electrical power. The efficiency of the reactor (i.e., efficiency of conversion of thermal energy into electrical energy) is 25%. What is the amount of ²³⁵U used in the reactor per year? The thermal energy released per fission of 235U is 200 MeV.
Answer: Rate of electrical energy generation is 250 MW = 250 × 10⁶ W (or J s^–1).

Question: When four hydrogen nuclei combine to form a helium nucleus estimate the amount of energy in MeV released in this process of fusion (Neglect the masses of electrons and neutrons).
Given:
(i) Mass of ¹₁ H = 1.007825 u
(ii) mass of helium nucleus = 4.002603 u,1u = 931 MeV/c2

Answer: Energy released = Δm × 931 MeV
Δm= 4m(¹₁H )-m⁴₂He
Energy released
Δm =4m(¹₁H)- m (⁴₂He)]X931MeV
= [4 × 1.007825 – 4.002603] × 931 MeV = 26.72 MeV.

Question: In a typical nuclear reaction, e.g.
²₁H+²₁H→³₂He+¹₀n+3.27MeV,
although number of nucleons is conserved, yet energy is released. How? Explain.
Answer: In a given nuclear reaction, the sum of the masses of the target nucleus (21H) and the bombarding particle (21H) may be greater than the product nucleus (³₂He) and the outgoing neutron ₀ ¹n. So from the law of conservation of mass-energy some energy (3.27 MeV) is released due to mass defect in the nuclear reaction. This energy is called Q-value of the nuclear reaction.

Question: Distinguish between the phenomena of nuclear fission and fusion.
Answer: 

Long Answer Type Questions 
Question: Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A Y-ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident g-ray. If E = B, show that this cannot happen.
Hence, calculate how much E should be bigger than B for such a process to happen.
Answer:  Applying principle of conservation of energy,