Please refer to Assignments Class 12 Physics Atoms Chapter 12 with solved questions and answers. We have provided Class 12 Physics Assignments for all chapters on our website. These problems and solutions for Chapter 12 Atoms Class 12 Physics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Atoms Assignments Class 12 Physics
Question: The transition from the state n = 3 to n = 1 in a hydrogen like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from
(a) 2 → 1
(b) 3 → 2
(c) 4 → 2
(d) 4 → 3
Answer:
D
Question: Rutherford’s experiments suggested that the size of the nucleus is about
(a) 10–14 m to 10–12 m
(b) 10–15 m to 10–13 m
(c) 10–15 m to 10–14 m
(d) 10–15 m to 10–12 m
Answer:
C
Question: In a hydrogen atom the total energy of electron is

Answer:
C
Question: The first model of atom in 1898 was proposed by
(a) Ernest Rutherford
(b) Albert Einstein
(c) J. J. Thomson
(d) Niels Bohr
Answer:
C
Question: In the Geiger-Marsden scattering experiment the number of scattered particles detected are maximum and minimum at the scattering angles respectively at
(a) 0°° and 180°°
(b) 180°° and 0°°
(c) 90°° and 180°°
(d) 45°° and 90°°
Answer:
A
Question: Which of the following is not correct about Bohrs model of the hydrogen atom?
(a) An electron in an atom could revolve in certain stable orbits without the emission of radiant energy.
(b) Electron revolves around the nucleus only in those orbits for which angular momentum
Ln=nh/2π .
(c) When electron make a transition from one of its stable orbit to lower orbit then a photon emitted with energy hu = Ef – Ei.
(d) Bohr model is applicable to all atoms.
Answer:
D
Question: The relation between the orbit radius and the electron velocity for a dynamically stable orbit in a hydrogen atom is (where, all notations have their usual meanings)
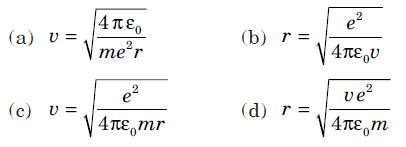
Answer:
C
Question: An electron in a hydrogen atom makes a transition from n = n1 to n = n2. The time period of the electron in the initial state is eight times that in the final state. The possible values of n1 and n2 are
(a) n1 = 4, n2 = 2
(b)n1 = 8, n2 = 2
(c) n1 = 8, n2 = 1
(d)n1 = 6, n2 = 2
Answer:
A
Question: The shortest wavelength present in the Paschen series of spectral lines is
(a) 720 nm
(b) 790 nm
(c) 800 nm
(d) 820 nm
Answer:
D
Question: A 10 kg satellite circles earth once every 2 h in an orbit having a radius of 8000 km.
Assuming that Bohr ’s angular momentum postulate applies to a satellite just as it does to an electron in the hydrogen atom, then the quantum number of the orbit of satellite is
(a) 5.3 × 1040
(b) 5.3 × 1045
(c) 7.8 × 1048
(d) 7.8 × 1050
Answer:
B
Question: If an electron in hydrogen atom is revolving in a circular track of radius 5.3 × 10–11 m with a velocity of 2.2 × 106 m s–1 around the proton then the frequency of electron moving around the proton is
(a) 6.6 × 1012 Hz
(b) 3.3 × 1015 Hz
(c) 3.3 × 1012 Hz
(d) 6.6 × 1015 Hz
Answer:
D
Question: The value of ionisation energy of the hydrogen atom is
(a) 3.4 eV
(b) 10.4 eV
(c) 12.09 eV
(d) 13.6 eV
Answer:
D
Question: The Rydberg formula, f or the spectrum of the hydrogen atom where all terms have their usual meaning is
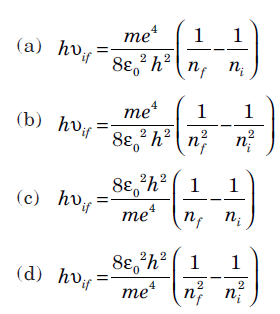
Answer:
B
Question: Energy is absorbed in the hydrogen atom giving absorption spectra when transition takes place from
(a) n = 1 → n′ where n′ > 1
(b) n = 2 → 1
(c) n′ → n
(d) n → n′ = ∞
Answer:
A
Question: In which of the following systems will the radius of the first orbit (n = 1) be minimum ?
(a) Doubly ionized lithium.
(b) Singly ionized helium.
(c) Deuterium atom.
(d) Hydrogen atom.
Answer:
A
Question: In the Geiger-Marsden scattering experiment, in case of head-on collision the impact parameter should be
(a) maximum
(b) minimum
(c) infinite
(d) zero
Answer:
B
Question: In a Geiger-Marsden experiment. Find the distance of closest approach to the nucleus of a 7.7 MeV a-particle before it comes momentarily to rest and reverses its direction.
(Z for gold nucleus = 79)
(a) 10 fm
(b) 20 fm
(c) 30 fm
(d) 40 fm
Answer:
C
Question: The radius of nth orbit rn in terms of Bohr radius (a0) for a hydrogen atom is given by the relation
(a) na0
(b) √na0
(c) n2a0
(d) n3a0
Answer:
C
Question: The moment of momentum for an electron in second orbit of hydrogen atom as per Bohr’s model is
(a) h/π
(b) 2h
(c)2h/π
(d)π/ h
Answer:
A
Question: In an atom the ratio of radius of orbit of electron to the radius of nucleus is
(a) 103
(b) 104
(c) 105
(d) 106
Answer:
C
Very Short Answer Type Questions
Question: When is Hα line of the Balmer series in the emission spectrum of hydrogen atom obtained?
Answer : Hα line of the Balmer series in the emission spectrum of hydrogen atoms obtained when the transition occurs from n = 3 to n = 2 state.
Question: Why is the classical (Rutherford) model for an atom of electron orbiting around the nucleus not able to explain the atomic structure?
Answer : According to electromagnetic theory, electron revolving around the nucleus are continuously accelerated. Since an accelerated charge emits energy, the radius of the circular path of a revolving electron should go on decreasing and ultimately it should fall into the nucleus. So, it could not explain the structure of the atom. As matter is stable, we cannot expect the atoms to collapse.
Question: Find the radius and energy of a He+ ion in the states n = 2.
Answer : r=0.5292n/Z
r(n=2) 0 .529×22/2=1.058Å
E(n=2)=-13.6×22/22=-13.6ev
Question: State Bohr ’s quantization condition of angular momentum.
Answer: Bohr’s quantization condition : The electron can revolve round the nucleus only in those circular orbits in which angular momentum of an electron is an integral multiple i.e..,mvr=nh/2π,n=1,2,3,….
Question: What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state?
Answer: Number of spectral lines obtained due to transition of electron from n = 4 (3rd excited state) to n = 1 (ground state) is N = (4)(4 -1)/2=6

Short Answer Type Questions
Question:Would the Bohr formula for the H-atom remain unchanged if proton had a charge
(+4/3)e and electron a charge (–3/4)e, where e = 1.6 × 10–19C. Give reasons for your answer.
Answer: In Bohr’s formula,
mv2/r=1/4π εo(e)(-e)
Force ∝ (–e) (e) = –e2
If charge on proton is [+ 4/3e]and charge on electron is
[-3/4e], then their product [4/3e][ -3/4e]=-e2
Thus Bohr Formula remains the same
Question: Using Bohr model, calculate the electric current created by the electron when the H-atom is in the ground state.
Answer: Let a0 = Bohr radius.
v0 = velocity of electron in first orbit.
∴ Time taken by electron to complete one revolution
T=2πa0/v0
∴ Current created by electron, I =e/T
= e/[2πao/vo]= evo/2πao
Question:The kinetic energy of the electron orbiting in the first excited state of hydrogen atom is 3.4 eV.
Determine the de Broglie wavelength associated with it.
Answer:

Question: Consider a gas consisting Li++ (which is hydrogen like ion).
(i) Find the wavelength of radiation required to excite the electron in Li++ from n = 1 and n = 3.
(ii) How many spectral lines are observed in the emission spectrum of the above excited system?
Answer:
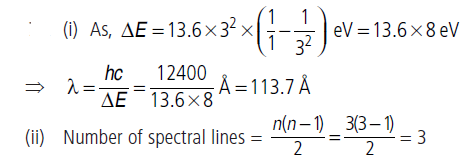
Question: Show that the first few frequencies of light that is emitted when electrons fall to the nth level from levels higher than n, are approximate harmonics (i.e. in the ratio 1 : 2 : 3…) when n > >1.
Answer:

Question: What is the minimum energy that must be given to a H atom in ground state so that it can emit an Hγ line in Balmer series. If the angular momentum of the system is conserved, what would be the angular momentum of such Hγ photon?
Answer: In Balmer series, Hγ line corresponds to transition from
state ni = 5 to state nf = 2.
Energy required, E = E5 – E1
=[13.6/52]-[13.6/12]=13.06 eV.
If angular momentum of system is conserved,change in angular momentum of electron = change in angular momentum of photon
=5[h/2π[-2[h/2π]=3h/2π
=3×6.6×10-34/2×3.14=3.17×1034 J s
Question: Assume that their is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb’s law as usual. Under such circumstances, calculate the ground state energy of a He-atom.
Answer: There are two protons and two neutrons in helium atom.
Two electrons are revolving around the nucleus in first orbit.
It is assumed that there is no interaction between the two electrons to He-atom.
so, replacing Z = 1 by Z = 2
En=[-13.6Z2/n2]ev,
For ground state (n = 1) of helium atom, energy
E1=[-13.6/122]eV=-54.4eV
Helium has two electrons in ground state, so total energy
E = 2E1 = –108.8 eV.
Question: A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelengths of the first member of Lyman and first member of Balmer series.
Answer: Here, ΔE = 12.5 eV
Energy of an electron in nth orbit of hydrogen atom is,
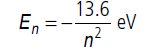
In ground state, n = 1
E1 = –13.6 eV
Energy of an electron in the excited state after absorbing a photon of 12.5 eV energy will be

Here, state of electron cannot be in fraction.
So, n = 3 (2nd excited state).
The wavelength λ of the first member of Lyman series is given by

The wavelength λ′ of the first member of the Balmer series
is given by

Question: The electron in a given Bohr orbit has a total energy of –1.5 eV. Calculate its
(i) kinetic energy.
(ii) potential energy.
(iii) wavelength of radiation emitted, when this
electron makes a transition to the ground state.
[Given : Energy in the ground state = –13.6 eV
and Rydberg’s constant = 1.09 × 107 m–1]
Answer:
(i) The kinetic energy (Ek) of the electron in an orbit is equal to negative of its total energy (E).
Ek = –E = – (–1.5) = 1.5 eV
(ii) The potential energy (Ep) of the electron in an orbit is equal to twice of its total energy (E).
Ep = 2E = –1.5 × 2 = –3.0 eV
(iii) Here, ground state energy of the H-atom = –13.6 eV
When the electron goes from the excited state to the ground state, energy emitted is given by
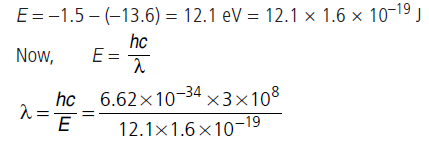
λ = 1.025 × 10–7 = 1025 Å
Question: (i) How does de-Broglie hypothesis explain Bohr ’s quantization condition for stationary orbits ?
(ii) Find the relation between the three wavelengths λ1, λ2 and λ3 from the energy level diagram shown in the figure.
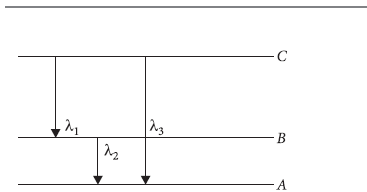
Answer: (i) de-Broglie hypothesis may be used to derive Bohr’s formula by considering the electron to be a wave spread over the entire orbit, rather than as a particle which at any instant is located at a point in its orbit. The stable orbits in an atom are those which are standing waves. Formation of standing
waves require that the circumference of the orbit is equal in length to an integral multiple of the wavelength. Thus, if r is the radius of the orbit
2πr = nλ = nh/p s [∴ λ=h/p]
which gives the angular momentum quantization
L=pr= n h/ 2π

which is the required relation between the three given wavelengths.
Question: Show that the radius of the orbit in hydrogen atom varies as n2, where n is the principal quantum number of the atom.
Answer: Radius of nth orbit of hydrogen atom : In H-atom, an electron having charge –e revolves around the nucleus of charge +e in a circular orbit of radius r, such that necessary centripetal force is provided by the electrostatic force of attraction between the electron and nucleus.
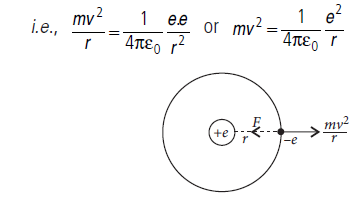

where n = 1, 2, 3, … is principal quantum number.
Equation (iii), gives the radius of nth orbit of H-atom. So the radii of the orbits increase proportionally with n2 i.e.,
[r ∝ n2]. Radius of first orbit of H-atom is called Bohr radius a0 and is given by
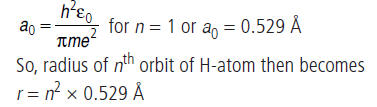
Long Answer Type Questions
Question: In the Auger process an atom makes a transition to a lower state without emitting a photon. The excess energy is transferred to an outer electron which may be ejected by the atom.
(This is called an Auger electron). Assuming the nucleus to be massive, calculate the kinetic energy of an n = 4 Auger electron emitted by Chromium by absorbing the energy from a n = 2 to n = 1 transition.
Answer: As the nucleus is massive, recoil momentum of the atom can be ignored. We can assume that the entire energy of transition is transferred to the Auger electron.
As there is a single valence electron in chromium (Z = 24),the energy states may be thought of as given by Bohr model.
The energy of the nth state is

Question: (a) Write two important limitations of Rutherford model which could not explain the observed features of atomic spectra.
(b) How were these explained in Bohr’s model of hydrogen atom?
Answer: (a) (i) Limitation of Rutherford’s model :
Rutherford’s atomic model is inconsistent with classical physics. According to electromagnetic theory, an electron is a charged particle moving in the circular orbit around the nucleus and is accelerated, so
it should emit radiation continuously and thereby loose energy. Due to this, radius of the electron would decrease continuously and also the atom should then produce continuous spectrum, and ultimately electron will fall into the nucleus and atom will collapse in 10–8 s. But the atom is fairly stable and it emits line spectrum.
(ii) Rutherford’s model is not able to explain the spectrum of even most simplest H-spectrum.
(b) Bohr’s postulates to resolve observed features of atomic spectrum :
(i) Quantum condition: Of all the possible circular orbits allowed by the classical theory, the electrons are permitted to circulate only in those orbits in which the angular momentum of an electron is an integral multiple of h/2π ,hbeing Planck’s constant. Therefore, for any permitted orbit, L mvr=nh/2π n = 123……,
where n is called the principal quantum number, and this equation is called Bohr’s quantisation condition.
(ii) Stationary orbits: While revolving in the permissible orbits, an electron does not radiate energy. These nonradiating orbits are called stationary orbits.
(iii) Frequency condition: An atom can emit or absorb radiation in the form of discrete energy photons only when an electron jumps from a higher to a lower orbit or from a lower to a higher orbit, respectively.
hυ = Ei – Ef where v is frequency of radiation emitted, Ei and Ef are the energies associated with stationary orbits of principal quantum number ni and nf respectively (where ni > nf).
Case Based MCQs
Electron Transitions for the Hydrogen Atom
Read the Bohr’s model explains the spectral lines of hydrogen atomic emission spectrum. While the electron of the atom remains in the ground state, its energy is unchanged. When the atom absorbs one or more quanta of energy, the electrons moves from the ground state orbit to an excited state orbit that is farther away.
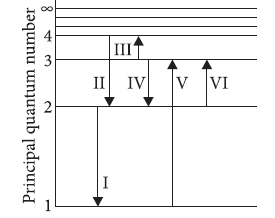
The given figure shows an energy level diagram of the hydrogen atom. Several transitions are marked as I, II, III and so on. The diagram is only indicative and not to scale.
Question: The wavelength of the radiation involved in transition II is
(a) 291 nm
(b) 364 nm
(c) 487 nm
(d) 652 nm
Answer:
C
Question: In which transition is a Balmer series photon absorbed?
(a) II
(b) III
(c) IV
(d) VI
Answer:
D
Question: Which transition will occur when a hydrogen atom is irradiated with radiation of wavelength 1030 nm?
(a) I
(b) II
(c) IV
(d) V
Answer:
D
Hydrogen Emission Spectrum
Hydrogen spectrum consists of discrete bright lines in a dark background and it is specifically known as hydrogen emission spectrum. There is one more type of hydrogen spectrum that exists where we get dark lines on the bright background, it is known as absorption spectrum.
Balmer found an empirical formula by the observation of a small part of this spectrum and it is represented by 1/λ=R[1/22-1/n2],where n = 3, 4, 5, ….. .
For Lyman series, the emission is from first state to nth state, for Paschen series, it is from third state to nth state, for Brackett series, it is from fourth state to nth state and for Pfund series, it is from fifth state to nth state.
Question: Which series of hydrogen spectrum corresponds to ultraviolet region?
(a) Balmer series
(b) Brackett series
(c) Paschen series
(d) Lyman series
Answer:
D
Question: Number of spectral lines in hydrogen atom is
(a) 8
(b) 6
(c) 15
(d) ∞
Answer:
D
Question: Rydberg constant is
(a) a universal constant
(b) same for same elements
(c) different for different elements
(d) none of these.
Answer:
A
Question: Which of the following lines of the H-atom spectrum belongs to the Balmer series?
(a) 1025 Å
(b) 1218 Å
(c) 4861 Å
(d) 18751 Å
Answer:
C
