Please refer to Assignments Class 11 Mathematics Conic Sections Chapter 11 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 11 Conic Sections Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Conic Sections Assignments Class 11 Mathematics
Question. The length of transverse axis of the hyperbola 3x2 – 4y2 = 32, is
(a) 8√2/√3
(b) 16√2/√3
(c) 3/32
(d) 64/3
Answer
A
Question. The equation of the hyperbola with vertices (3, 0), (–3, 0) and semi-latus rectum 4 is given by :
(a) 4x2 – 3y2 + 36 = 0
(b) 4x2 – 3y2 + 12 = 0
(c) 4x2 – 3y2 – 36 = 0
(d) 4x2 + 3y2 – 25 = 0
Answer
C
Question. The eccentricity of an ellipse, with its centre at the origin, is . 1/2 If one of the directrices is x = 4, then the equation of the ellipse is:
(a) 4x2 + 3y2 = 1
(b) 3x2 + 4y2 = 12
(c) 4x2 + 3y2 = 12
(d) 3x2 + 4y2 = 1
Answer
B
Question. The eccentricity of the curve 2x2 + y2 – 8x – 2y + 1= 0 is:
(a) 1/2
(b) 1/√2
(c) 2/3
(d) 3/4
Answer
B
Question. Radius of the circle (x + 5)2 + (y – 3)2 = 36 is
(a) 2
(b) 3
(c) 6
(d) 5
Answer
C
Question. The value of p such that the vertex of y = x2 + 2px +13 is4 units above the y-axis is
(a) 2
(b) ± 4
(c) 5
(d) ± 3
Answer
D
Question. The two conics y2/b2 + x2/a2= 1 and y2 = − b/a x intersect if and only if
(a) 0 < a ≤ 1/2
(b) 0 < b ≤ 1/2
(c) b2 > a2
(d) b2 < a2
Answer
B
Question. If the equation of ellipse is 9x2 + 4y2 = 36, then

Codes
A B C D
(a) 4 1 3 2
(b) 2 1 3 4
(c) 4 3 1 2
(d) 2 3 1 4
Answer
A
Question. If a parabolic reflector is 20 cm in diameter and 5 cm deep, then the focus is
(a) (2, 0)
(b) (3, 0)
(c) (4, 0)
(d) (5, 0)
Answer
D
Question. The foci of an ellipse are (±2, 0) and its eccentricity is 1/2 then the equation of ellipse is x2/a2 + y2/12= 1. The value of ‘a’ is
(a) 3
(b) 4
(c) 6
(d) 2
Answer
B
Question. The equation of a hyperbola with foci on the x-axis is
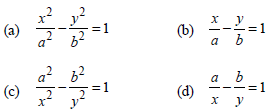
Answer
A
Question. The equation of a circle with centre at (1, 0) and circumference 10π units is
(a) x2 + y2 – 2x + 24 = 0
(b) x2 + y2 – x – 25 = 0
(c) x2 + y2 – 2x – 24 = 0
(d) x2 + y2 + 2x + 24 = 0
Answer
C
Question. A circle has radius 3 and its centre lies on the line y = x−1. The equation of the circle, if it passes through (7, 3), is
(a) x2 + y2 + 8x − 6y +16 = 0
(b) x2 + y2 − 8x + 6y +16 = 0
(c) x2 + y2 − 8x − 6y −16 = 0
(d) x2 + y2 − 8x − 6y +16 = 0
Answer
D
Question. The equation of the hyperbola whose foci are (– 2, 0) and (2, 0) and eccentricity is 2 is given by :
(a) x2 – 3y2 = 3
(b) 3x2 – y2 = 3
(c) – x2 + 3y2 = 3
(d) – 3x2 + y2 = 3
Answer
B
Question. The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
(a) x2 + y2 = 9a2
(b) x2 + y2 = 16a2
(c) x2 + y2 = 4a2
(d) x2 + y2 = a2
Answer
C
Question. Tangents are drawn from the point (–2, –1) to the parabola y2 = 4x. If α is the angle between these tangent then the value of tan α is
(a) 3
(b) 4
(c) –5
(d) 5
Answer
A
Question. Which points on the curve x2 = 2y are closest to the point (0, 5) ?
(a) (± 2√2,4)
(b) (± 2,2)
(c) (± 3,9/2)
(d) (± 2,1)
Answer
A
Question. Intercept on the line y = x by the circle x2 + y2 − 2x = 0 is AB. Equation of the circle on AB as a diameter is
(a) x2 + y2 + x − y = 0
(b) x2 + y2 − x + y = 0
(c) x2 + y2 + x + y = 0
(d) x2 + y2 − x − y = 0
Answer
D
Question. The equation 9x2 – 16y2 – 18x + 32y – 151 = 0 represents a hyperbola
(a) The length of the transverse axes is 4
(b) Length of latus rectum is 9
(c) Equation of directrix is x = 21/5 and x = –11/5
(d) None of these
Answer
C
Question. The length of the line segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line segment makes an angle Θ to the x-axis is 4am/n. Here, m and n respectively are
(a) sin Θ, cos Θ
(b) cos Θ, sin Θ
(c) cos Θ, sin2Θ
(d) sin2Θ, cos Θ
Answer
C
Question. For the parabola y2 = –12x, equation of directrix is x = a. The value of ‘a’ is
(a) 3
(b) 4
(c) 2
(d) 6
Answer
A
Question. Equation of the hyperbola whose directrix is 2x + y = 1, focus (1, 2) and eccentricity √3 is
(a) 7x2 – 2y2 + 12xy – 2x + 9y – 22 = 0
(b) 5x2 – 2y2 + 10xy + 2x + 5y – 20 = 0
(c) 4x2 + 8y2 + 8xy + 2x – 2y + 10 = 0
(d) None of these
Answer
A
Question. Length of the latus rectum of the hyperbola : x2/a2 − y2/b2 = 1 is
(a) b2/a
(b) 2b2/a
(c) a2/b
(d) 2a2/b
Answer
B
Question. Equation of the circle concentric with the circle x2 + y2 – 3x + 4y – c = 0 and passing through the point (–1, – 2), is
(a) x2 + y2 − 3x − 4y = 0
(b) x2 + y2 − 3x + 4y = 0
(c) x2 + y2 + 3x + 4y = 0
(d) x2 + y2 – 7x + 7y = 0
Answer
B
Question. The equation y2 + 3 = 2(2x+ y) represents a parabola with the vertex at
(a) (1/2,1)and axis parallel to y-axis
(b) (1,1/2) and axis parallel to x-axis
(c) (1/2,1) and focus at (3/2,1)
(d) (1,1/2) and focus at (3/2,1)
Answer
C
Question. What is the radius of the circle passing through the points (0, 0), (a, 0) and (0, b) ?

Answer
C
Question. Equation of the circle which passes through the intersection of x2 + y2 + 13x – 3y = 0 and 2x2 + 2y2+ 4x – 7y – 25 = 0 whose centre lies on 13x + 30y = 0 is
(a) x2 + y2 + 5x + y = 0
(b) 4x2 + 4y2 + 30x −13y − 25 = 0
(c) 2x2 + 2y2 + 3x − 4y = 0
(d) 4x2 + 4y2 − 8x + 7y +10 = 0
Answer
B
Question. The eccentricities of the ellipse x2/α2 + y2/β2 = 1, α > β; and x2/9 + y2/16= 1 are equal. Which one of the following is correct ?
(a) 4α = 3β
(b) αβ =12
(c) 4β = 3α
(d) 9α =16β
Answer
A
Question. A focus of an ellipse is at the origin. The directrix is the line x = 4 and the eccentricity is 1/2 . Then the length of the semimajor axis is
(a) 8/3
(b) 2/3
(c) 4/3
(d) 5/3
Answer
A
Question. The equation of the circle in the first quadrant touching each coordinate axis at a distance of one unit from the origin is
(a) x2 + y2 – 2x – 2y + 1 = 0
(b) x2 + y2 – 2x – 2y – 1 = 0
(c) x2 + y2 – 2x – 2y = 0
(d) x2 + y2 – 2x + 2y – 1 = 0
Answer
A
Question. The equation of the ellipse whose axes are along the co-ordinate axes, vertices are (±5, 0) and foci at (±4, 0), is x2/25 + y2/b2 = 1. The value of b2 is
(a) 3
(b) 5
(c) 9
(d) 4
Answer
C
Question. The circle x2 + y2 – 8x + 4y + 4 = 0 touches :
(a) x-axis only
(b) y-axis only
(c) both (a) and (b)
(d) None of these
Answer
B
Question. The distance between the foci of a hyperbola is 16 and its eccentricity is √2. Its equation is
(a) x2 – y2 = 32
(b) x2/4 – y2/9 = 1
(c) 2x – 3y2 = 7
(d) None of these
Answer
A
Question. The eccentricity of the ellipse whose major axis is three times the minor axis is:
(a) √2/3
(b) √3/2
(c) 2√2/3
(d) 2/√3
Answer
C
Question. The equation of an ellipse with one vertex at the point (3, 1), the nearer focus at the point (1, 1) and e = 2/3 is :
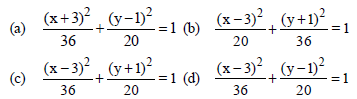
Answer
D
Question. If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then radius of the circle is
(a) 3/4
(b) 2/3
(c) 1/4
(d) 5/2
Answer
A
Question. The locus of a point P(α, β) moving under the condition that the line y = αx +β is a tangent to the hyperbola x2/a2− y2/b2 = 1
(a) an ellipse
(b) a circle
(c) a parabola
(d) a hyperbola
Answer
D
Question. The equation of the circle with centre (0, 2) and radius 2 is x2 + y2 – my = 0. The value of m is
(a) 1
(b) 2
(c) 4
(d) 3
Answer
C
Question. Match the foci, centre, transverse axis, conjugate axis and vertices of hyperbola given in column-I with their corresponding meaning given in column-II
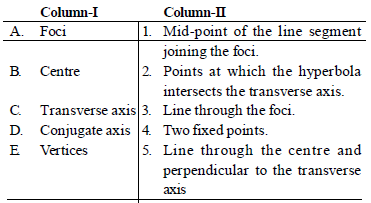
Codes
A B C D E
(a) 4 3 1 5 2
(b) 1 4 3 5 2
(c) 4 1 5 3 2
(d) 4 1 3 5 2
Answer
D
Question. The point diametrically opposite to the point P(1, 0) on the circle x2 + y2 + 2x + 4y – 3 = 0 is
(a) (3, – 4)
(b) (–3, 4)
(c) (–3, –4)
(d) (3, 4)
Answer
C
Question. Four distinct points (2k, 3k), (1, 0), (0, 1) and (0, 0) lie on a circle for
(a) only one value of k
(b) 0 < k < 1
(c) k < 0
(d) all integral values of k
Answer
A
Question. The vertex of the parabola x2 + 8x + 12y + 4 = 0 is:
(a) (– 4, 1)
(b) (4, –1)
(c) (– 4, –1)
(d) (4, 1)
Answer
A
Question. The lines 2x − 3y = 5 and 3x − 4y = 7 are diameters of a circle having area as 154 sq.units.Then the equation of the circle is
(a) x2 + y2 − 2x + 2y = 62
(b) x2 + y2 + 2x − 2y = 62
(c) x2 + y2 + 2x − 2y = 47
(d) x2 + y2 − 2x + 2y = 47 .
Answer
D
Question. If (2, 0) is the vertex and the y-axis is the directrix of a parabola, then its focus is
(a) (0, 0)
(b) (– 2, 0)
(c) (4, 0)
(d) (– 4, 0)
Answer
C
Question. An ellipse has OB as semi minor axis, F and F ‘ its focii and the angle FBF ‘ is a right angle. Then the eccentricity of the ellipse is
(a) 1/√2
(b) 1/2
(c) 1/4
(d) 1/√3
Answer
A
STATEMENT TYPE QUESTIONS
Question. If equation of the ellipse is x2/100+ y2/400 = 1, then
I. Vertices of the ellipse are (0, ± 20)
II. Foci of the ellipse are (0, ±10√3)
III. Length of major axis is 40.
IV. Eccentricity of the ellipse is √3/2.
(a) I and II are true.
(b) III and IV are true.
(c) II, III, IV are true.
(d) All are true.
Answer
D
Question. Consider the following statements.
I. Length of the latus rectum of the ellipse x2/a2 + y2/b2 = 1 is 2b2/a
II. A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. I. The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.
II. The points of intersection of the conic section and the axis are called vertices of the conic section.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
I. The two fixed points are called the foci of the ellipse.
II. The mid point of the line segment joining the foci is called the centre of the ellipse.
III. The end points of the major axis are called the vertices of the ellipse.
(a) Only I and II are correct.
(b) Only II and III are correct.
(c) Only I and III are correct.
(d) All are correct.
Answer
D
Question. Consider the following statements.
I. A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
II. A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line) in the plane.
(a) Only I is true
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. The centre of the circle 2r = 2 − 4r cosθ + 6 r sinθ is:
(a) (2, 3)
(b) (– 2, 3)
(c) (– 2, – 3)
(d) (2, – 3)
Answer
B
Question. The point (2, 3) is a limiting point of a co-axial system of circles of which x1 + y2 = 9 is a member. The coordinates of the other limiting point is given by:
(a) (18/13 , 27/13)
(b) (9/13 , 6/13)
(c) (18/13 , –27/13)
(d) (–18/13 , –9/13)
Answer
A
Question. In the co-axial system of circle x2 + y2 + 2gx + c = 0 where g is a parameter, if c > 0. Then the circles are:
(a) Orthogonal
(b) Touching type
(c) Intersecting type
(d) Non intersecting type
Answer
D
Question. The equation of a circle of radius 1 touching the circles x2 + y2 − 2|x|= 0 is:
(a) x2 + y + 2 3x − 2= 0
(b) x2 + y − 2 3y + 2= 0
(c) x2 + y + 2 3y + 2= 0
(d) x + y + 2 3x + 2= 0
Answer
B,C
Question. The number of integral values of λ for which x2 + y2 +λ x + (1−λ ) y + 5 = 0 is the equation of a circle whose radius cannot exceed 5, is:
(a) 14
(b) 18
(c) 16
(d) 20
Answer
C
Question. If circles x2 + y2 + 2ax + c = 0 and x2 + y2 + 2bx + c = 0 touch each other, then:
(a) 1/a + 1/b = 1/c
(b) 1/a2 + 1/b2 = 1/c2
(c) 1/a + 1/b = c2
(d) 1/a2 + 1/b2 = 1/c
Answer
D
Question. If two circles (x−1)2 + ( y−3)2 =r and x2 + y2 −8x+2y+8=0 intersect in two distinct points, then:
(a) 2 < r < 8
(b) r = 0
(c) r < 2
(d) r > 2
Answer
A
Question. The equation of the circle whose radius is 5 and which touches the circle x2 + y2 − 2x − 4y − 20 = 0 externally at the point (5, 5), is:
(a) x2 + y2 −18x −16y −120 = 0
(b) x2 + y2 −18x −16y +120 = 0
(c) x2 + y2 +18x +16y −120 = 0
(d) x2 + y2 +18x −16y +120 = 0
Answer
B
Question. Centre of circle (x − x1)(x − x2) +( y − y1)( y − y2) = 0 is:
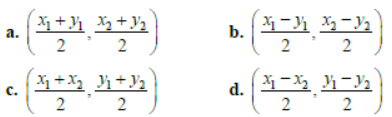
Answer
C
Question. The centre of the circle, which cuts ortho-gonally each of the three circles x2 + y2 +2x+17 y+4=0, x2 + y2 +7x+6y+11=0 and x2 + y2 − x + 22y + 3 = 0 is:
(a) (3, 2)
(b) (1, 2)
(c) (2, 3)
(d) (0, 2)
Answer
A
Question. The equation of the circle through the points of intersection of the circles x2 + y2 – 6x + 2y + 4 = 0, x2 + y2 + 2x – 4y – 6 = 0 and with its centre on the line y = x ?
(a) 7x2 + 7y2 +10x −10y −12 = 0
(b) 7x2 + 7y2 −10x −10 y −12 = 0
(c) 7x2 + 7y2 −10x +10y −12 = 0
(d) 7x2 + 7y2 +10x +10 y +12 = 0
Answer
B
Question. The equation of the circle in the first quadrant touching each coordinate axis at a distance of one unit from the origin is:
(a) x2 + y2 − 2x − 2y +1 = 0
(b) x2 + y2 − 2x − 2y −1 = 0
(c) x2 + y2 − 2x − 2y = 0
(d) None of these
Answer
A
Question. The equation of the circle passing through the point (−1, − 3) and touching the line 4x + 3y −12 = 0 at the point (3, 0), is:
(a) x2 + y2 − 2x + 3y − 3 = 0
(b) x2 + y2 + 2x − 3y − 5 = 0
(c) 2x2 + 2y2 − 2x + 5y −8 = 0
(d) None of these
Answer
A
Question. The of circle passing through (3,–6) and touching both the axes is
(a) x2 + y2 − 6x + 6y + 9 = 0
(b) x2 + y2 + 6x − 6y + 9 = 0
(c) x2 + y2 + 30x − 30y + 225 = 0
(d) x2 + y2 − 30x + 30y + 225 = 0
Answer
A,D
Question. Equation of a circle with centre (4, 3) touching the circle x2 + y2 =1 is
(a) x2 + y2 −8x − 6y − 9 = 0
(b) x2 + y2 −8x − 6y +11 = 0
(c) x2 + y2 −8x − 6y −11 = 0
(d) x2 + y2 −8x − 6y + 9 = 0
Answer
C,D
Question. For the circle x2 + y2 + 6x −8y + 9 = 0 , which of the following statements is true:
(a) Circle passes through the point (−3, 4)
(b) Circle touches x-axis
(c) Circle touches y-axis
(d) None of these
Answer
D
Question. The locus of the centre of the circle which cuts a chord of length 2a from the positive x-axis and passes through a point on positive y-axis distant b from the origin is:
(a) x2 + 2by = b2 + a2
(b) x2 − 2by = b + a
(c) x2 + 2by = a −b
(d) x2 − 2by = b − a
Answer
B
Question. The equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y − 4x + 3 = 0 , is:
(a) x2 + y2 + 4x −10y + 25 = 0
(b) x2 + y2 − 4x −10y + 25 = 0
(c) x2 + y2 − 4x −10y +16 = 0
(d) x2 + y2 −14y + 8 = 0
Answer
B
Question. A circle is concentric with the circle x + y − 6x +12y +15 = 0 and has area double of its are(a)
The equation of the circle is:
(a) x2 + y2 − 6x +12y −15 = 0
(b) x2 + y2 − 6x +12y +15 = 0
(c) x2 + y2 − 6x +12y + 45 = 0
(d) None of these
Answer
A
Question. The range of values of a for which the point (a, 4) is outside the circles x2 + y2 +10x = 0 and x2 + y2 −12x + 20 = 0 is:
(a) (−∞,−8)∪(−2,6)∪(6,+∞)
(b) (– 8, – 2)
(c) (−∞,−8)∪(−2,+∞)
(d) None of these
Answer
A
Question. If the common chord of the circles x2 + (y – λ)2 = 16 and x2 – y2 = 16 subtend a right angle at the origin, then λ is equal to:
(a) 4
(b) 4√2
(c) ± 4√2
(d) 8
Answer
C
Question. The equation of the image of the circle x2 + y2 + 16x – 24y + 183 = 0 by the line mirror 4x + 7y + 13 = 0 is:
(a) x2 + y2 + 32x − 4 y + 235 = 0
(b) x2 + y2 + 32x + 4y − 235 = 0
(c) x2 + y2 + 32x − 4 y − 235 = 0
(d) x2 + y2 + 32x + 4y + 235 = 0
Answer
D
Question. If the circles x2 + y2 = a and x2 + y2 − 2gx + g − b = 0 touch each other externally, then:
(a) g = ab
(b) g2 = a2 + b2
(c) g2 = ab
(d) g = a + b
Answer
D
Question. The abscissae of A and B are the roots of the equation x2 + 2ax − b2 = 0 and their ordinates are the roots of the equation y2 + 2by − q2 = 0. The equation of the circle with AB as diameter is:
(a) x2 + y2 + 2ax + 2by − b2 − q2 = 0
(b) x2 + y2 + 2ax + by − b2 − q2 = 0
(c) x2 + y2 + 2ax + 2by + b2 + q2 = 0
(d) None of these
Answer
A
Question. If the straight line y = mx is outside the circle x2 + y2 − 20 y + 90 = 0, then:
(a) m > 3
(b) m < 3
(c) | m | > 3
(d) | m | < 3
Answer
D
