MCQ Questions Chapter 7 Coordinate Geometry 10 Mathematics

Please refer to MCQ Questions Chapter 7 Coordinate Geometry Class 10 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 10 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 10 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 7 Coordinate Geometry in Class 10 Mathematics provided below to get more marks in exams.

Chapter 7 Coordinate Geometry MCQ Questions

Please refer to the following Chapter 7 Coordinate Geometry MCQ Questions Class 10 Mathematics with solutions for all important topics in the chapter.

MCQ Questions Answers for Chapter 7 Coordinate Geometry Class 10 Mathematics

Question. One diagonal of a square is the portion of the line 3x + 2y = 12 intercepted between the axes. The coordinates of the extremity of the other diagonals not lying in the first quadrant are
(a) (1, − 1)
(b) (− 1, − 1)
(c) (− 1, 1)
(d) none of these

Question. The join of the points (− 3, − 4) and (1, − 2) is divided by y-axis in the ratio.
(a) 1 : 3
(b) 2 : 3
(c) 3 : 1
(d) 3 : 2

Question. Mid-points of the sides AB and AC of ΔABC are (3, 5) and (−3, −3) respectively, then the length of BC =
(a) 10
(b) 15
(c) 20
(d) 30

Question. The following points A(−1, 0), B(3,1), C(2,2) and D(−2,1) taken in order form a
(a) rectangle
(b) parallelogram
(c) square
(d) None

Question. Area of the rhombus enclosed by the lines ax ± by ± c = 0 is
(a) 2a²/bc
(b) 2b²/ca
(c) 2c²/ab
(d) None

Question. Find the value of k, if the distance between the points (1,4) and (k, 1) is 5.
(a) 3 or 5
(b) − 3 or 5
(c) 3 or − 5
(d) None

Question. Write an equation for a line passing through the points (c, 2b) and (c,3b).
(a) y = cx − b
(b) y = − cx + b
(c) x = 2b
(d) x = c

Question. The points (k − 1, k + 2), (k, k + 1), (k + 1, k) are collinear for
(a) any value of k
(b) k = −1/2 only
(c) no value of k
(d) integral values of k only

Question. The line x/3 +y/4 = 1 meets the axis of y and axis of x at A and B respectively. A square ABCD is constructed on the line segment AB away from the origin, the coordinates of the vertex of the square farthest from the origin are
(a) (7, 3)
(b) (4, 7)
(c) (6, 4)
(d) (3, 8)

Question. ABC is an isosceles triangle with B = (1, 3) and C = (−2, 7) then A =
(a) (5/6, 6)
(b) (6, 5/6)
(c) (7, 1/8)
(d) None of these

Question. ABCD is a quadrilateral. P (3, 7) and Q (7, 3) are the middle points of the diagonals AC and BD respectively. The coordinates of the mean point (or the centre of mean position) of the vertices of the quadrilateral are
(a) (0, 0)
(b) (3, 3)
(c) (5, 5)
(d) (7, 7)

Question. The centroid of a triangle lies at the origin and the coordinates of its two vertices are (− 8, 0) and (9, 11), the area of the triangle in sq. units is
(a) 11 / 8
(b) 8/11
(c) 88
(d) None

Question. The area of a triangle, two of whose vertices are (2, 1) and (3, − 2) is 5. The coordinates of the third vertex can not be
(a) (6, − 1)
(b) (4, 5)
(c) (− 1, 20)
(d) (2, 9)

Question. The coordinates of the points A and B are respectively (– 3, 2) and (2, 3). P and Q are points on the line joining A and B such that AP = PQ = QB. A square PQRS is constructed on PQ as one side, the coordinates of R are
(a) (−4/3, 7/3)
(b) (0, 13/3)
(c) (1/3, 8/3)
(d) (2/3, 1)

Question. If A(at², 2at), B(a/t², − 2a/t) and S (a, 0) are three points, then 1/ + 1/SB is independent of
(a) a
(b) t
(c) both a and t
(d) none of these

Question. The area of the triangle formed by the points (k, 2 − 2k), (− k + 1, 2k) and (− 4 − k, 6 − 2 k) is 70 units. For
(a) four real values of k
(b) no integral value of k
(c) two integral values of k
(d) only one integral value of k

Question. ABCD is a square in which A lies on the positive y-axis and B lies on the positive x-axis. If D is the point (12, 17), the coordinates of C are
(a) (17 , 12)
(b) (17 , 5)
(c) (14 , 16)
(d) (15, 3)

Question. What type of triangle is formed by the points P(√2, √2), Q (−√2, −√2) and R(−√6,√6) ?
(a) Scalene triangle
(b) equilateral triangle
(c) Isosceles triangle
(d) None of these

Question. ABCD is a rhombus. Its diagonals AC and BD intersect at the point M and satisfy BD = 2AC. If the coordinates of D and M are (1, 1) and (2, − 1) respectively, the coordinates of A are
(a) (− 3, − 1/2)
(b) (1, − 3/2)
(c) (3/2, − 1)
(d) (1/2, − 3)

Question. If the straight lines x + 2y − 9 = 0, 3x + 5y − 5 = 0 and ax + by + 1 = 0 are concurrent, then the straight line 35x − 22y − 1 = 0 passes through
(a) (a, b)
(b) (b, a)
(c) (a, − b)
(d) (− a, b)

Question. The points (0, 8/3), (1, 3) and (82, 30) are the vertices of
(a) obtuse angled triangle
(b) acute angled triangle
(c) right angled triangle
(d) none of these

Question. A ray of light coming from the point (1, 2) is reflected at a point A on the axis of x and then passes through the point (5, 3). The coordinates of the point A are
(a) (5/13, 0)
(b) (−7, 0)
(c) (13/5, 0)
(d) (15, 0)

Question. The number of lines that can be drawn through the point (4, − 5) at a distance 12 from the point(− 2, 3) is
(a) 0
(b) 1
(c) 2
(d) Infinite

Question. If O is the origin and the coordinates of A and B are (x₁, y₁) and (x₂, y₂) respectively then OA × OB cos Ð AOB is equal to
(a) x₁y₁ + x₂y₂
(b) x₁x₂ + y₁ y₂
(c) x₁y₂ + x2y₁
(d) x₁x₂ − y₁y₂

Question. If the points (x, 4) lies on a circle whose centre is at the origin and radius is 5, then x=
(a) ± 5
(b) ± 3
(c) 0
(d) ± 4

Question. The ratio in which the line segment joining P (x₁, −y₁) and Q (x₂,y₂) is divided by x-axis is:
(a) y₁: y₂
(b) −y₁ : y₂
(c) x₁ : x₂
(d) −x₁ : x₂

Question. The line 3x + 2y = 24 meets the y-axis at A and the x-axis at B ; C is a point on the perpendicular bisector of AB such that the area of the triangle ABC is 91 sq. units. The coordinates of C can be
(a) (29/2, − 1)
(b) (29/2, 13)
(c) (− 13/2, 1)
(d) (− 13/2, 13)

Question. If (−2, 1) is centroid of the triangle having its vertices at (x, 0), (5,−2), (−8, y), then x,y satisfy the relation
(a) 5x+3y=0
(b) 3x−8y=0
(c) 8x+3y=0
(d) 8x=3y

Question. Line formed by joining (−1, 1) and (5,7) is divided by a line x + y = 4 in the ratio of
(a) 1 : 2
(b) 1 : 3
(c) 3 : 4
(d) 1 : 4

Question. The area of triangle formed by the points (p, 2 − 2p), (1 − p, 2p) and (−4 − p, 6 − 2p) is 70 sq. units. How many integral value of p are possible ?
(a) 2
(b) 3
(c) 4
(d) None of these

Question. Which of the following is TRUE regarding the graphs of the equations of a linear quadratic sys- tem ?
(a) the graphs may intersect in two locations
(b) the graphs may intersect in one location
(c) the graphs may not intersect
(d) all three choice are true

Question. The midpoints of sides of a triangle are (3, 4), (4, 1) and (2, 0). Which of the following does not denote the co-ordinates of its vertices ?
(a) 1, 3
(b) 5, 3
(c) 5, 5
(d) 3, −3

Question. If the line segment joining the points (3,−4) and (1, 2) is trisected at points P (a,−2) and Q(5/3,b) , then
(a) a= 8/3, b= 2/3
(b) a =7/3 ,b=0 
(c) a= 1/3, b=1 
(d) a =2/3, b= 1/3 

Question. The point which lies on the perpendicular bisector of the line sequence joining the points P(−2, 0) and Q(2, 5) is :-
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) (−2, 0)

Question. Point P divides the line segment joining the points A (2, 1) and (5, −8) such that AP/AB =1/3 . If P lies on the line 2x−y+k=0, find the value of k.
(a) 2
(b) −2
(c) 4
(d) −4

Question. In what ratio is the line segment joining the point (−2, −3) and (3, 7) divided by y-axis ?
(a) 3 : 2
(b) 5 : 2
(c) 2 : 3
(d) 2 : 5

Question. The centre of a circle is (2a, a−7). Find the values of a, if the circle passes through points (11,−9) and has diameter 10√2units
(a) 2 or 3
(b) 3 or 4
(c) 4 or 2
(d) 3 or 5

Question. If points (a, 0), (0, b) and (1, 1) are collinear, then (a+b)/ab equals :-
(a) 1
(b) −1
(c) 2
(d) 2

Question. The point which divides the line segment joining the points (3, 4) and (7, −6) in the ratio 1 : 2 internally lies in the_________quadrant.
(a) I
(b) II
(c) III
(d) IV

Question. If the vertices of a triangle ABC are A (− 4, − 1), B (1, 2) and C (4, − 3), then the coordinates of the circumcentre of the triangle are
(a) (1/3, − 2/3)
(b) (0, − 4)
(c) (0, − 2)
(d) (− 3/2, 1/2)

Question. The extremities of a diagonal of a parallelogram are the points (3, − 4) and (− 6, 5). If third vertex is (− 2, 1) then the coordinates of the fourth vertex are
(a) (1, 0)
(b) (0, 0)
(c) (1, 1)
(d) None

Question. The point (22, 23) divide the join of P(7, 5) and Q externally in the ratio 3 : 5, then Q =
(a) (3, 7)
(b) (−3, 7)
(c) (3, −7)
(d) (−3, −7)

Question. The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x+3. Find the coordinates of the third vertex.
(a) (13/2,7/2) or (−3/2,3/2)
(b) (7/2,13/2) or (3/3,−3/2)
(c) (2/7,2/13) or (2/3,−2/3) 
(d) (7/2,13/2) or (−3/2,3/2)

Question. The centroid of a triangle formed by (7, p), (q, −6), (9, 10) is (6, 3), then (p, q) =
(a) (4, 5)
(b) (5, 4)
(c) (−5, −2)
(d) (5, 2)

Question. The third vertex of an equilateral triangle whose two vertices are (2, 4), (2, 6) is :
(a) ( √3 , √5)
(b) (2 √3 , 5)
(c) (2+√ 3 , 5)
(d) (2, 5)

Question. The mid points of the sides AB and AC of a triangle ABC are (2, − 1) and (− 4, 7) respectively, then the length of BC is
(a) 10
(b) 20
(c) 25
(d) 30

Question. If the area of the triangle given below is 20, then what are the coordinates of the point C ?

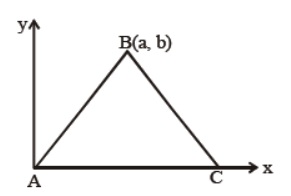
(a) (0, 40/a)
(b) (a² + b², 0)
(c) (20/b, 0)
(d) (40/b, 0)

Question. If the coordinates of two points A and B are (3, 4) and (5, −2) respectively. Find the coordinates of any points P, if PA=PB and area of ΔPAB=10.
(a) (7, 1) or (0, 1)
(b) (7, 2) or (1, 0)
(c) (2, 7) or (1, 0)
(d) (2, 7) or (0, 1)

Question. The quadrilateral ABCD formed by the points A (0, 0), B (3, 4), C (7, 7) and D (4, 3) is a
(a) rectangle
(b) square
(c) rhombus
(d) parallelogram

Question. Find the area of a rhombus, if its vertices are (3, 0) (4, 5), (−1, 4) and (−2, −1), taken is order.
(a) 21
(b) 22
(c) 24
(d) 23

Question. The triangle with vertices A (2, 7), B (4, y) and C(− 2, 6) is right angled at A if  
(a) y = −1
(b) y = 0
(c) y = 1
(d) None

Question. The centroid of a triangle lies at the origin and the coordinates of its two vertices are (−8, 7) and (9, 4). The area of the triangle is
(a) 95/6
(b) 285/2
(c) 190/3
(d) 285

Question. A postman walks towards North a distance of 120 m to deliver a letter. He then goes towards East for a distance of 50 m for delivering another letter. The shortest distance between the two places is
(a) 70 m
(b) 120 m
(c) 130 m
(d) 170 m

Question. If a point (x, y) is equidistant from the points (p + q, q – p) and (p – q, p + q), then ________     
(a) qx + yp = 0 
(b) qx = yp 
(c) px = qy 
(d) px + qy = 0 
(e) None of these

Question. If A (7/3 , m/5) is the midpoint of the line segment joining the points B (3, -2) and C (4, 6), then the value of m is _______   
(a) 4
(b) 10
(c) – 4
(d) – 8
(e) None of these

Question. The orthecentre of the triangle formed by the lines , 5x – 8y = 10 , 16x + 10y = 13 and y-axis, is _____     
(a) (102/89 , -95/178)
(b) (51/89 , 89/95)
(c) (102/89 , 95/178)
(d) (51/89 , -95/89)
(e) None of these

Question. The area of a triangle, whose vertices are (a, a – 2), (a + 2, a + 2) and (a + 3, a), is _________   
(a) 1 sq unit
(b) 2 sq units
(c) 3 sq units
(d) 4 sq units
(e) None of these

Question. The radius of the circle which passes through the origin (0, 6) and (6, 0) is     
(a) 12cm
(b) 6 cm
(c) 3√2 cm
(d) 4√2
(e) None of these

Question. If the points (p, 0), (0, q) and (1, 1) are collinear, then 1/p + 1/q equals to _______     
(a) 1 unit
(b) 2 unit
(c) 3 unit
(d) 4 unit
(e) None of these

Question. The length of the side of a at the of the angle of Pythagorean triangle of 8 cm, 15 cm 17 cm the hypotenuse is ________   
(a) 5, 5/23 cm
(b) 6, 4/23 cm
(c) 7, 3/23 cm
(d) 4, 2/23 cm
(e) None of these

Question. The ratio, in which the line 5x + 3y = – 9 divides the segment joining the points (2, 3) and (- 3, 4), is ________   
(a) 4 : 3
(b) – 4 : 3
(c) – 14 : 5
(d) – 14 : 3
(e) None of these

Question. If a point A (-1, 3) divides internally the line segment joining B (3, 4) and ( in ratio 2 : 3, then the coordinates of point C is ______   
(a) (2,-3)
(b) (2, 3/2 )
(c) (-1 , 2/3)
(d) (-2, 3)
(e) None of these

Question. The area of a triangle formed by the line 4x – 3y + 12 0 with the coordinate axes is __________     
(a) 3 sq unit
(b) 4 sq unit
(c) 5 sq unit
(d) 6 sq unit
(e) None of these

Question. Find the area of the quadrilateral whose vertices , taken in order are (−4, −2,) (−3, −5) (3,−2) and (2, 3).
(a) 20 sq. unit
(b) 28 sq. unit
(c) 30 sq. unit
(d) 38 sq. unit

(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.

Question. Assertion : The points (k, 2 – 2k), (– k+ 1, 2k) and (– 4 – k, 6 – 2k) are collinear if k = 1/ 2 .   
Reason : Three points A, B and C are collinear in same straight line, if AB + BC = AC.

Question. Assertion : If A(2a, 4a) and B(2a, 6a) are two vertices of an equilateral triangle ABC then, the vertex C is given by (2a + √a 3,5a) .   
Reason : In equilateral triangle, all the coordinates of three vertices can be rational.

Question. Assertion : Mid-point of a line segment divides line in the ratio 1 : 1.     
Reason : If area of triangle is zero that means points are collinear.

One Word Questions :

Question. What is the length of the line AB, where A (1, 0) and B (5, 3).

Question. In the figure ABCD, is a rhombus. Find the coordinates of the point D.

Question. What is distance between points ( –3, 2) and (1, –2)?

Question. Find the coordinates of the fourth point B such that OABC forms a square and coordinates of O, A and C being (0, 0), (3, 0) and (0, 3).

Question. Find the length of the line AB, where coordinates of points A and B are (2, 7) and (–2, 4).

Question. If (p, q) is the mid-point of (5, 3) and (–2, –4) find the value of p + q.

Question. The three vetices of a rhombus taken in order are (–2, –1), (3, 4) and (–2, 3). Find the fourth vertex.

Question. What is the distance of the point (8, –2) from the origin?

Question. Gunjan walks 12m due east and then 5m due north. At what distance is Gunjan from the starting point?

Question. If two adjacent vertices of parallelogram are (3, 2), (–1, 0) and the diagonals cut at (2, –5) find the coordinates of other vertices of the parallelogram.

Question. The mid-point of the line segement joining (3p, 4) and (–2, 2q) is (2, 6). Find the value of p.

Question. Find the distance of the point (0, 2) from the mid-point of the line joining (4, 10) and (2, 2).

Question. Find the value of x such that Q is the mid-point of PR and coordinates of P, Q and R are (6, –2), (1, 3) and (x, 8) respectively.

Question. The line segment joining the points (3, –4) and (1, 2) is trisected at the points P and Q. Find the coordinates of P.

Question. Point Q lies on the line joining origin and P in such a way that OP = OQ. What will be the co-ordinates of Q, if coordinates of P are (–3,2).

Question. In which ratio is the line joining the points A(–4, 4) and B(7, 7) divided by (0, –1)?

Question. If AB is the line joining (0, 1) and (4, –2) and CD is the line joining (1, 2) and (6, 4), then what is CD² – AB²?

Question. Find the sum of lengths of AB and BC if the coordinates of A, B and C are (1, 2), (–2, –2) and (4, 6) respectively.

Question. The line segment joining the points (–4, 0) and (0, 6) is divided into four equal parts at P, Q and R. Find the coordinates of Q.

Question. Find the value of k if the point (0, 3) is equidistant from (5, k) and (k, k).

Question. What is the distance between the points (–2, 4) and (–4, 3)?

Question. In the figure, M is the mid-point of AB. Find the coordintes of B.

Question. What is the area of triangle formed by the points (3, 0), (0, 4), and (0, 0)?

Question. In which quadrant does the point (–10, 2) lie?

Question. Find the length of median AD of the triangle formed by the points A(0,6), B(8, 0) and C(4, 2).

We hope you liked the above provided MCQ Questions Chapter 7 Coordinate Geometry Class 10 Mathematics with solutions. If you have any questions please ask us in the comments box below.