MCQ Questions Chapter 6 Triangles Class 10 Mathematics

Please refer to MCQ Questions Chapter 6 Triangles Class 10 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 10 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 10 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 6 Triangles in Class 10 Mathematics provided below to get more marks in exams.

Chapter 6 Triangles MCQ Questions

Please refer to the following Chapter 6 Triangles MCQ Questions Class 10 Mathematics with solutions for all important topics in the chapter.

MCQ Questions Answers for Chapter 6 Triangles Class 10 Mathematics

Question. In the given figure, if DE || BC, the EC equals

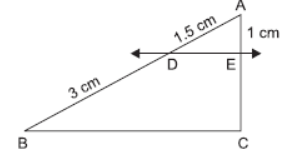
(a) 1 cm
(b) 2 cm
(c) 4 cm
(d) 6 cm

Question. In the given figure, if LM || CB and LN || CD, then AM/ MB equals

(a) AN /ND
(b) AD/ ND
(c) AL/ AN
(d) None of these

Question. In the given figure, ∠D = ∠E and AD/ DB = AE/ EC , then triangle BAC is a/an

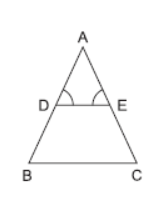
(a) Scalene triangle
(b) Isosceles triangle
(c) Equilateral triangle
(d) None of these

Question. In the figure shown along side, DE || BC, ∠ADE = 70° and ∠BAC = 50°, then ∠BCA =

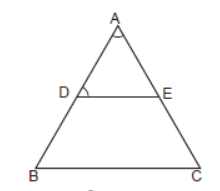
(a) 30°
(b) 60°
(c) 40°
(d) 45°

Question. In the figure, if ∠ACB = ∠CDA, AC = 6 cm and AD = 3 cm, then the length of AB is

(a) 8 cm
(b) 10 cm
(c) 12 cm
(d) 16 cm

Question. In the given figure, if PQ || AB and AQ || CB, then that AR² =

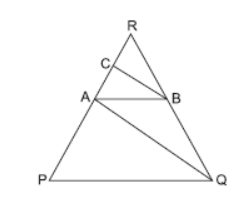
(a) PR + CR
(b) PR·CR
(c) PR – CR
(d) None of these

Question. If in two triangles DEF and PQR, –D = –Q and –R = –E, then which of the following is not true?
(a) EF/PR = DF/PQ
(b) DE/PQ = EF/RP
(c) DE/QR = DF/PQ
(d) EF/RP = DE/QR

Question. In ΔABC and ΔDEF, ∠B =∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar

Question. In the ΔABC, D and E are points on side AB and AC respectively such that DE || BC. If AE = 2 cm, AD = 3 cm and BD = 4.5 cm, then CE equals
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm

Question. In the given figure, D and E are points on AB and AC respectively such that DE || BC. If AD = 1/3 BD and AE = 4.5 cm, then AC is equal to

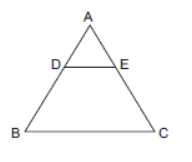
(a) 12 cm
(b) 14 cm
(c) 16 cm
(d) 18 cm

Question. In given figure figure, DE || BC. If AD/ DB = 3/ 2 and AE = 2.7 cm, then EC is equal to

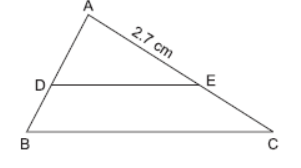
(a) 2.0 cm
(b) 1.8 cm
(c) 4.0 cm
(d) 2.7 cm

Question. In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Choose the correct choice as:

(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): If ∆ABC and ∆PQR are congruent triangles, then they are also similar triangles.
Reason (R): All congruent triangles are similar but the
similar triangles need not be congruent.
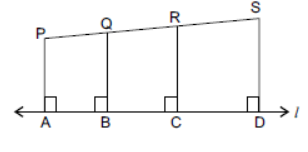
2. Assertion (A): In the given figure, PA || QB || RC || SD.
Reason (R): If three or more line segments are perpendiculars to one line, then they are parallel to each other.

Question. The perimeters of two similar triangles ΔABC and ΔPQR are 35 cm and 45 cm respectively, then the ratio of the areas of the two triangles is     
(a) 7 : 9
(b) 28 : 45
(c) 14 : 27
(d) 49 : 81

Question. In the given figure, ΔABC and ΔXYZ are shown. If AB = 3 cm, BC = 8 cm, AC = 2√3 cm, ∠A = 80°, ∠B = 60°, XY = 4 √3 cm, YZ = 12 cm and XZ = 6 cm, then the value of ∠Y is   

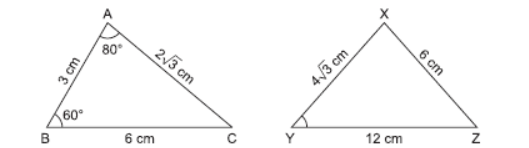
(a) 10°
(b) 40°
(c) 35°
(d) 75°

Question. Given ΔABC ~ ΔPQR, if AB/ PQ = 1/ 3 , then ar(ΔABC)/ ar(ΔPQR)  =     
(a) 1 : 3
(b) 1 : 6
(c) 1 : 9
(d) 1 : 5

Question. In the given figures, ΔPQR ∼ ΔXYZ. If PQ = 4 cm, QR = 5 cm and XY = 6 cm, then YZ equals.     

(a) 4.5 cm
(b) 7.5 cm
(c) 6.4 cm
(d) None of these

Question. Given ΔABC~ΔPQR, if PQ/ AB = 1/3 , then ar(ΔABC)/ ar(ΔPQR)  is   
(a) 1/ 9
(b) 1/ 11
(c) 2/ 5
(d) 5 /9

Question. If in two triangles ABC and PQR, AB/ QR = BC/ PR = CA/ PQ , then     
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR

Question. In the given figure, DE || BC, AD = 1 cm and BD = 2 cm. What is the ratio of the ar (∆ABC) to the ar (∆ADE)?   

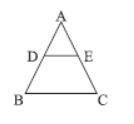
(a) 1 : 9
(b) 1 : 7
(c) 9 : 1
(d) 7 : 1

Question. In the given figure, DB ⊥ BC, DE ⊥ AB and AC ⊥ BC. Then BE/ DE =    

(a) AC/ AE
(b) AC/ DE
(c) BC/ DE
(d) AC/ BC

Question. ΔABC is isosceles with AC = BC. If AB² = 2AC², then the measure of ∠C is        
(a) 30°
(b) 60°
(c) 45°
(d) 90°

Question. The sides of two similar triangles are in the ratio 2 : 3, then the areas of these triangles are in the ratio     
(a) 2 : 5
(b) 4 : 9
(c) 7 : 16
(d) None of these

Question. Let ΔABC ∼ ΔDEF, ar (ΔABC) = 169 cm2 and ar (ΔDEF) = 121 cm². If AB = 26 cm, then DE equals     
(a) 11 cm
(b) 22 cm
(c) 33 cm
(d) 44 cm

Question. The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of the first triangle is 9 cm, then the corresponding side of second triangle is     
(a) 5.4 cm
(b) 8 cm
(c) 9.5 cm
(d) 10 cm

Question. In given figure, ST || RQ, PS = 3 cm and SR = 4 cm. The ratio of the area of ΔPST to the area of Δ PRQ is   

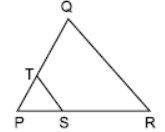
(a) 2 : 25
(b) 9 : 49
(c) 11 : 30
(d) 5 : 28

Question. If ΔPQR ~ ΔXYZ, ∠Q = 50° and ∠R = 70°, then ∠X + ∠Y is equal to   
(a) 70°
(b) 110°
(c) 120°
(d) 50°

Question. Corresponding sides of two similar triangles are in the ratio 9 : 5. Areas of these triangles are in the ratio 
(a) 21 : 85
(b) 81 : 25
(c) 9 : 5
(d) 5 : 9

Question. In the given figure, M is mid-point of side CD of a parallelogram ABCD. The line BM is drawn intersecting AC at L and AD produced at E. Then EL =     

(a) BL
(b) 1/ 2 BL
(c) 2BL
(d) None of these

Question. AD and PM are medians of triangles ABC and PQR respectively where ΔABC ∼ ΔPQR. Then PQ/ AB equals     
(a) AC MR
(b) AD MP
(c) AC PM
(d) AD QM

Question. In the given figure, ΔEFG is a square and ∠BAC = 90°. Then FG² =     

(a) BG × FC
(b) BG + FC
(c) BG/ FC
(d) None of these

Question. ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such tht PQ ll BC and divides ΔABC into two parts equal in area. Then AB/ BP is equal to     
(a) 2 + √2 : 2
(b) 2 − √2 : 2
(c) 2 + √3 : 3
(d) 2 − √3 : 3

Question. Right angled triangles BAC and BDC are right angled at A and D and they are on same side of BC. If AC and BD intersect at P, then AP × PC equals     
(a) PB × DP
(b) BD × DP
(c) AP × DP
(d) None of these

Question. In a trapezium ABCD, AC and BD intersecting at O, AB || DC and AB = 2CD, if area of ΔAOB = 84 cm², the area of ΔCOD is
(a) 12 cm²
(b) 18 cm²
(c) 21 cm²
(d) 27 cm²

Question. In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Choose the correct choice as:   

(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
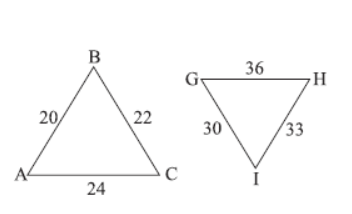
1. Assertion (A): In the given figures, ΔABC ~ ΔGHI.
Reason (R): If the corresponding sides of two triangles are proportional, then they are similar.
2. Assertion (A): The sides of two similar triangles are in the ratio 2 : 5, then the areas of these triangles are in the ratio 4 : 25.
Reason (R): The ratio of the areas of two similar triangles is equal to the square of the ratio of their sides.

Question. In ΔABC, AB = 6 √3 cm , AC = 12 cm and BC = 6 cm, then ∠B =   
(a) 30°
(b) 60°
(c) 90°
(d) 45°

Question. A ladder is placed against a wall such that its foot is at distance of 5 m from the wall and its top reaches a window 5 √3 m above the ground. The length of the ladder is   
(a) 10 m
(b) 15 m
(c) 18 m
(d) 24 m

Question. If in an equilateral triangle, the length of the median is 3 cm, then the length of the side of equilateral triangle is   
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm

Question. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1½ hours?   
(a) 100 √61 km
(b) 51 √61 km
(c) 300 √61 km
(d) None of these

Question. ABC is an isosceles triangle right-angled at C. The AB² is equal to   
(a) AC²
(b) 2AC
(c) AC²
(d) AC/2

Question. In ΔABC, ∠ABC = 90°. AD and CE are two medians drawn from A and C, respectively. If AC = 5 cm and AD = 3 √5/2 cm , the length of CE is   
(a) 2 √5 cm
(b) 3 √5 cm
(c) 4 √5 cm
(d) √5 cm

Question. A man goes 12 m due west and then 9 m due north. How far is he from the starting point ?      
(a) 12 m
(b) 15 m
(c) 18 m
(d) 24 m

Question. In an equilateal triangle of side 3 √3 cm, the length of the altitude is     
(a) 3.5 cm
(b) 4 cm
(c) 4.5 cm
(d) 6 cm

Question. From airport two aeroplanes start at the same time. If the speed of first aeroplane due North is 500 km/h and that of other due East is 650 km/h, then the distance between two aeroplanes after 2 hours will be   
(a) 100 km
(b) 100 √157 km
(c) 100 √269 km
(d) None of these

Question. In the given figure, ABCD is a rectangle. P is the mid-point of DC. If QB = 7 cm, AD = 9 cm and DC = 24 cm, then ∠APQ equals    

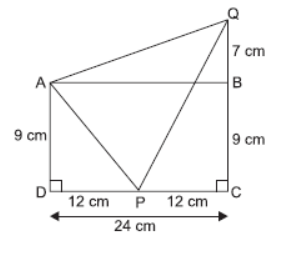
(a) 30°
(b) 60°
(c) 45°
(d) 90°

Question. If in ΔABC, AB = 9 cm, BC = 40 cm and AC = 41 cm, then the ΔABC is a/an   
(a) Acute angled triangle
(b) Right triangle
(c) Obtuse angled triangle
(d) Isosceles triangle

Question. In an isosceles triangle PQR, PQ = QR and PR² = 2PQ². Then ∠Q is   
(a) 30°
(b) 60°
(c) 90°
(d) None of these

Question. In ΔABC, ∠B = 90° and BD ⊥ AC. If AC = 9 cm and AD = 3 cm, then BD is equal to   
(a) 2 √2 cm
(b) 3 √2 cm
(c) 2 √3 cm
(d) 3 √3 cm

Question. In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Choose the correct choice as:    
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): If two sides of a right angle are 7 cm and 8 cm, then its third side will be 9 cm.
Reason (R): In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
2. Assertion (A): In the ∆ABC, AB = 24 cm, BC = 10 cm and AC = 26 cm, then ∆ABC is a right angle triangle.
Reason (R): If in two triangles, their corresponding angles are equal, then the triangles are similar.

We hope you liked the above provided MCQ Questions Chapter 6 Triangles Class 10 Mathematics with solutions. If you have any questions please ask us in the comments box below.