Please refer to MCQ Questions Chapter 12 Surface Area and Volume Class 10 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 10 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 10 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 12 Surface Area and Volume in Class 10 Mathematics provided below to get more marks in exams.
Chapter 12 Surface Area and Volume MCQ Questions
Please refer to the following Chapter 12 Surface Area and Volume MCQ Questions Class 10 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 12 Surface Area and Volume Class 10 Mathematics
Question. A medicine -capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of the entire capsule is 2 cm. the capacity of the capsule is:
(a) 0.36 cm3
(b) 0.35 cm3
(c) 0.34 cm3
(d) 0.33 cm3
Answer
A
Question. Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is
(a) 3:4
(b) 4:3
(c) 9:16
(d) 16:9
Answer
D
Question. A surahi is a combination of:
(a) a sphere and a cylinder
(b) a hemisphere and a cylinder
(c) two hemispheres
(d) a cylinder and a cone.
Answer
A
Question. A plumbline (Sahul) is a combination of (see the given figure)
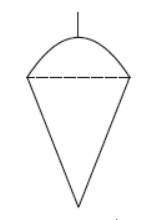
(a) a cone and a cylinder
(b) a hemisphere and a cone
(c) frustum of a cone and a cylinder
(d) sphere and cylinder
Answer
B
Question. The shape of a gilli, in the gilli-danda game (see the given figure), is a combination of

(a) two cylinders
(b) a cone and a cylinder
(c) two cones and a cylinder
(d) two cylinders and a cone
Answer
C
Question. A shuttle cock used for playing badminton has the shape of a combination of:
(a) a cylinder and a sphere
(b) a cylinder and a hemisphere
(c) a sphere and a cone
(d) frustum of a cone and a hemisphere
Answer
D
Question. The radius of a sphere (in cm) whose volume is 12p cm3, is:
(a) 3
(b) 3 3
(c) 32/3
(d) 31/3
Answer
C
Question. A cylindrical pencil sharpened at one edge is a combination of:
(a) a cone and a cylinder
(b) frustum of a cone and a cylinder
(c) a hemisphere and a cylinder
(d) two cylinders.
Answer
A
Question. A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that 1 8 space of the cuberemains unfilled. Then the number of marbles that the cube can accomodate is:
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Answer
A
Question. A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8cm. The height of the cone is:
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Answer
B
Question. If the radius of the sphere is increased by 100%, the volume of the corresponding sphere is increased by:
(a) 200%
(b) 500%
(c) 700%
(d) 800%
Answer
C
Question. The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is:
(a) 60p cm2
(b) 68p cm2
(c) 120p cm2
(d) 136p cm2
Answer
D
Question. The base radii of a cone and a cylinder are equal. If their curved surface areas are also equal, then the ratio of the slant height of the cone to the height of the cylinder is:
(a) 2 : 1
(b) 1 : 2
(c) 1 : 3
(d) 3 : 1
Answer
A
Question. A metallic sphere of diameter 20 cm is recast into a right circular cone of base radius 10 cm. What is the height of the cone?
(a) 4 cm
(b) 40 cm
(c) 60 cm
(d) 120 cm
Answer
D
Question. Three cubes each of side 15 cm are joined end to end. The total surface area of the cuboid is:
(a) 3150 cm2
(b) 1575 cm2
(c) 1012.5 cm2
(d) 576.4 cm2
Answer
A
Question. The lateral surface area of a cylinder is 176 cm2 and its base area is 38.5cm2 .What is its volume?
(a) 830 cm3
(b) 380 cm3
(c) 308 cm3
(d) 803 cm3
Answer
C
Question. A hemispherical bowl is made of steel of 0.25 cm thickness. The inner radius of the bowl is 5 cm. What is the volume of steel used?
(a) 42.15 cm3
(b) 41.52 cm3
(c) 41.25cm3
(d) 43.21cm3
Answer
C
Question. The ratio of the radii of two spheres is 3 : 2. Find the ratio of their volumes.
(a) 25 : 4
(b) 5 : 16
(c) 9 :14
(d) 27 : 8
Answer
D
Question. The diameter of a copper sphere is 6 cm. It is beaten and drawn into a wire of diameter 0.2 cm. What is the length of the wire?
(a) 36cm
(b) 360cm
(c) 3600 cm
(d) 306 cm
Answer
C
Question. A cone and a hemisphere have equal bases and equal volumes. Identify the ratio of their heights.
(a) 1 : 3
(b) 1 : 2
(c) 2 : 1
(d) 3 : 1
Answer
C
Question. The largest right circular cone is carved out of a cube whose edge is of length ‘p’ units. Find the volume of the cone.
(a) π p3/12 cu units
(b) π p3/4 cu units
(c) π p3 cu.units
(d) π p3 /5 cu units
Answer
A
Question. A right-angled triangle ABC, where∠B = 90o , is rotated about BC. If BC = 16 cm and AC = 20 cm, find the volume of the right circular cone traced out by the triangle.

(a) 2413cm3
(b) 2311 cm3
(c) 1254cm3
(d) 1725cm3
Answer
A
Question. The area of the base of a cone is 616 sq cm. Its height is 48 cm. Find its total surface area.
(a) 2816cm2
(b) 2861 cm2
(c) 2618cm2
(d) 2681 cm2
Answer
A
Question. The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume is 1/27 . the volume of cone, what is the height at which the section is made?
(a) 10 cm
(b) 15 cm
(c) 20 cm
(d) 19 cm
Answer
C
Question. A hemispherical bowl of internal diameter 36 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 3 cm and height 9 cm. How many bottles are required to empty the bowl?
(a) 24
(b) 35
(c) 12
(d) 48
Answer
D
Fill in the Blanks :
Question. The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 2 cm. The length of the wire is …………………….. .
Answer
36 cm
Question. A spherical metal ball of radius 8 cm is melted to make 8 smaller identical balls. The radius of each new ball is …………………….. cm.
Answer
4 cm
Question. The ratio between the volumes of two spheres is 8:27. Then, the ratio between their surface areas is …………………….. .
Answer
4 : 9
Question. If the radius of the base of a right circular cylinder is halved, keeping the height same, then the ratio of the volume of the reduced cylinder to that of the original cylinder is …………………….. .
Answer
1 : 4
Question. The total surface area of the given solid figure is ……………………..
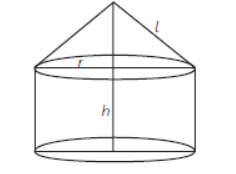
Answer
πrl + 2πrh + πr2
Question. If the length of each diagonal of a cube is doubled, then its volume become ……………. times.0
Answer
If the length of each diagonal of a cube is doubled, then its volume becomes eight times.
Question. A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is …………………….. .
Answer
2r
True or False :
Question. Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is 6πr2.
Answer
False
Question. A solid ball is exactly fitted inside a cubical box of side a. The volume of the ball is 4 /3 pa3 .
Answer
False
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
Question. Assertion: Total surface area of the cylinder having radius of the base 14 cm and height 30 cm is 3872 cm2.
Reason: If r be the radius and h be the height of the cylinder, then total surface area = (2πrh + 2πr2 ).
Answer
A
Question. Assertion: If a ball is in the shape of a sphere has a surface area of 221.76 cm2, then its diameter is 8.4 cm.
Reason: If the radius of the sphere be r, then surface area, S = 4πr2, i. e. r = 1/ 2√S/π .
Answer
A
Question. Assertion: If the height of a cone is 24 cm and diameter of the base is 14 cm, then the slant height of the cone is 15 cm.
Reason: If r be the radius and h the slant height of the cone, then slant height = √h2 + r2 .
Answer
D
Question. Assertion: No. of spherical balls that can be made out of a solid cube of lead whose edge is 44 cm, each ball being 4 cm. in diameter, is 2541
Reason : Number of balls = Volume of one ball /volumeof lead .
Answer
C

We hope you liked the above provided MCQ Questions Chapter 12 Surface Area and Volume Class 10 Mathematics with solutions. If you have any questions please ask us in the comments box below.


