Please refer to MCQ Questions Chapter 1 Relations and Functions Class 12 Mathematics with answers provided below. These multiple-choice questions have been developed based on the latest NCERT book for class 12 Mathematics issued for the current academic year. We have provided MCQ Questions for Class 12 Mathematics for all chapters on our website. Students should learn the objective based questions for Chapter 1 Relations and Functions in Class 12 Mathematics provided below to get more marks in exams.
Chapter 1 Relations and Functions MCQ Questions
Please refer to the following Chapter 1 Relations and Functions MCQ Questions Class 12 Mathematics with solutions for all important topics in the chapter.
MCQ Questions Answers for Chapter 1 Relations and Functions Class 12 Mathematics
Question. Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is (a) reflexive but not symmetric
(b) reflexive but not transitive
(c) symmetric and transitive
(d) neither symmetric, nor transitive
Answer
A
Question: The relation R defined in the set { 1,2,3,4,5,6} as R= {( a,b) : b=a+1} is
(a) reflexive
(b) symmetric
(c) transitive
(d) None of these
Answer
D
Question: The relation R in the set A = {1,2,3,4,5} is given by R={( a,b) :|a-b| is even}, is a/an
(a) equivalence relation
(b) only transitive
(c) reflexive and symmetric
(d) None of these
Answer
A
Question: The example of relation which are reflexive and transitive but not symmetric is
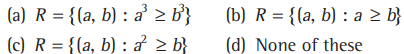
Answer
A
Question: The relation R in the set A {x ∈ Z:0 ≤x ≤ 12}. Given by, R = {(a, b) | a-b| is a multiple 4} is a/an
(a) only reflexive
(b) not reflexive
(c) equivalence relation
(d) None of these
Answer
C
Question: The relation R in the set A of all the books in a library of a college, given by R = {(x ,y x and y have same number of pages} is a/an
(a) reflexive
(b) reflexive and symmetric
(c) equivalence relation
(d) None of the above
Answer
C
Question: The relation R, defined in the set of A all triangles as R = {(T1T2) : T1 is similar to T2}. is a/an
(a) reflexive and symmetric
(b) only transitive
(c) equivalence relation
(d) None of these
Answer
C
Question: The relation R in the set A of points in a plane, given by R= {( P, Q) :distance of the point P from the origin is same as the distance of the point Q from the origin}, is a/an
(a) equivalence relation
(b) only symmetric
(c) not reflexive
(d) None of these
Answer
A
Question: Let R be the relation in the set {1,2,3,4} given by R = {(1,2), (2,2), (1,1), (4,4), (1,3), (3,3), (3,2)}.
(a) R is reflexive and symmetric but not transitive
(b) R is reflexive and transitive but not symmetric
(c) R is symmetric and transitive but not reflexive
(d) R is an equivalence relation
Answer
B
Question: Let L be the set of all lines in xy-plane and R be the relation in L defined as R{( L1,L2) : L1 is parallel to L2}, then R is a/an
(a) reflexive
(b) symmetric
(c) transitive
(d) equivalence relation
Answer
D
Question: Let A = {1,2, 3}. Then, number of relations containing ( 1,2) and (1,3) which are reflexive and symmetric but not transitive is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question: Let A = {1,2,3}. Then, number of equivalence relations containing (1,2) is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question: Given a non-empty set X. Consider P (X), which is the set of all subset of X. Defined the relation R in P (X ) as follows For subsets A and B in P (X), ARB if and only if A ⊂ B, then R is
(a) an equivalence relation on P (X)
(b) not an equivalence relation on P (X )
(c) a anti-symmetric
(d) None of the above
Answer
B
Question: The function f (x) is defined in [0,1], then the domain of definition of the function f[log(1-x2)] is
(a) x ∈ [- {0}
(b) x ∈ [- √1+e,-1] ∪ [1+√1+e]
(c) x ∈ (∞,∞)
(d) None of the above
Answer
A
Question:

Answer
D
Question: If D is the domain of the function sec−1(log x), then D contains
(a) (−∞1/e
(b) e −1
(c) 1
(d) None of these
Answer
D
Question: The domain of the function f (x)=1/1- tan x is
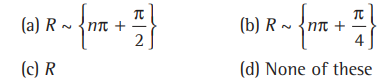
Answer
D
Question: The domain of the function f(x)= log 0.2 log 0.5 log 0.25 x is equal to
(a) (1, ∞)
(b) 1/4, ∞)
(c) (1/4,1)
(d) None of these
Answer
C
Question: Domain of f (x ) =sin-1[2-4x2]([⋅] denotes the greatest integer function) is
(a) [–1, 1]
(b) (–2, 2)
(c) [−√3/2,0) ∪(0,√3/2]
(d) None of these
Answer
C
Question
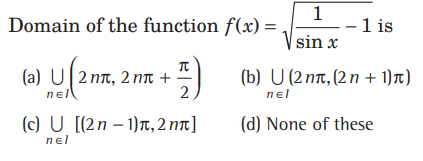
Answer
B
Question: The domain of the function F(x)=1/[x]+√2x-x2 is
(a) [1, 2]
(b) [0 ,2]
(c) [0, 1]
(d) [1, 0]
Answer
A
Question:
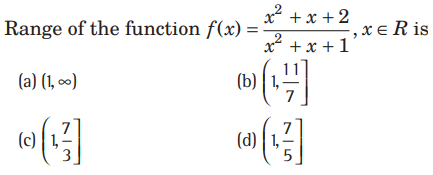
Answer
C
Question. Let R be a relation defined on Z as R= {(a,b) ; a2+b2=25 } , the domain of R is;
(a) {3,4,5}
(b) {0,3,4,5}
(c) {0,3,4,5,-3,-4,-5}
(d) none
Answer
C
Question. Let f : R –{3/5} → R be defined by f(x) = 3x+2/5x-3 . Then
(a) f –1(x) = f(x)
(b) f –1(x) = – f(x)
(c) (fof )x = – x
(d) f –1(x) = 1/19 f(x)
Answer
A
Question. If R = {(x, y) : x is exactly 7 cm taller than y}, then R is
(a) not symmetric
(b) reflexive
(c) symmetric but not transitive
(d) an equivalence relation
Answer
A
Question. The function f: R → R given by f(x) = x3 – 1 is
(a) a one-one function
(b) an onto function
(c) a bijection
(d) neither one-one nor onto
Answer
C
Question. Let * be a binary operation on set Q of rational numbers defined as a * b = ab/5 . The identity for * is
(a) 5
(b) 3
(c) 1
(d) 6
Answer
A
Question. The function f : [0, π] → R, f (x) = cos x is
(a) one-one function
(b) onto function
(c) a many one function
(d) None of these
Answer
A
Question. Let * be the binary operation on N given by a * b = HCF (a, b) where, a, b ∈ N. The value of 22 * 4 is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on set A = {1, 2, 3} is
(a) Reflexive but not symmetric
(b) Reflexive but not transitive
(c) Symmetric and transitive
(d) Neither symmetric nor transitive
Answer
A
Question. If g(x) = x – 2 is the inverse of the function f(x) = x + 2, then graph of g (x) is the image of graph of f(x) about the line y = kx. Here k =
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. If f(x) = ex and g(x) = logex, then which of the following is true?
(a) f {g (x)} ≠ g{f (x)}
(b) f {g (x)} = g{f (x)}
(c) f {g (x)}+ g{f (x)} = 0
(d) f {g (x)}- g{f (x)} =1
Answer
B
Question. Let X = {0, 1, 2, 3} and Y = {–1, 0, 1, 4, 9} and a function f :X → Y defined by y = x2, is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d) many-one into
Answer
B
Question. If f : R → R and g : R → R defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the value of x for which f(g(x)) = 25 is
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 4
Answer
B
Question. If f: R → R is given by
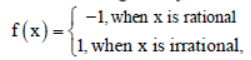
then (fof) (1- √3 ) is equal to
(a) 1
(b) – 1
(c) √3
(d) 0
Answer
B
Question. Which of the following functions from Z into Z are bijective?
(a) f(x) = x3
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f(x) = x2 + 1
Answer
B
Question. Let A = {1, 2, 3} and B = {2, 4, 6, 8}.
Consider the rule f : A → B, f(x) = 2x ∀ x ∈ A. The domain, codomain and range of f respectively are
(a) {1, 2, 3}, {2, 4, 6}, {2, 4, 6, 8}
(b) {1, 2, 3}, {2, 4, 6, 8}, {2, 4, 6}
(c) {2, 4, 6, 8}, {2, 4, 6, 7}, {1, 2, 3}
(d) {2, 4, 6}, {2, 4, 6, 8}, {1, 2, 3}
Answer
B
Question. The function f : A → B defined by f(x) = 4x + 7, x ∈ R is
(a) one-one
(b) many-one
(c) odd
(d) even
Answer
A
Question. The smallest integer function f(x) = [x] is
(a) one-one
(b) many-one
(c) Both (a) & (b)
(d) None of these
Answer
B
Question. A relation R in a set A is called symmetric, if for all a1, a2 ∈ A and (a2, a3)∈ R implies
(a) (a1, a2) ∈ R ∈ (a2, a1) ∈ R
(b) (a1, a2) ∈ R ∈ (a1, a1) ∈ R
(c) (a1, a2) ∈ R ∈ (a2, a2) ∈ R
(d) None of these
Answer
A
Question. Let f : R → R, g : R → R be two functions such that f(x) = 2x – 3, g(x) = x3 + 5. The function (fog)–1 (x) is equal to
(a) (x+7/2)1/3
(b) (x-7/2)1/3
(c) (x-2/7)1/3
(d) (x-7/2)1/3
Answer
D
Question. The relation R = { (1, 1), (2, 2), (3, 3)} on the set {1, 2, 3} is :
(a) symmetric only
(b) reflexive only
(c) an equivalence relation
(d) transitive only
Answer
B
Question. Let A be the non-empty set of children in a family. The relation ‘x is brother of y’ in A is:
(a) reflexive
(b) symmetric
(c) transitive
(d) None of these
Answer
C
Question. Let us define a relation R in R as aRb if a ≥ b. Then R is
(a) an equivalence relation
(b) reflexive, transitive but not symmetric
(c) symmetric, transitive but not reflexive
(d) neither transitive nor reflexive but symmetric
Answer
B
Question. Given set A = {a, b, c). An identity relation in set A is
(a) R = {(a, b), (a, c)}
(b) R = {(a, a), (b, b), (c, c)}
(c) R = {(a, a), (b, b), (c, c), (a, c)}
(d) R= {(c, a), (b, a), (a, a)}
Answer
B
Question. Let f : [0, ∞) → [0, 2] be defined by f(x)=2x/1+x, then f is
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
Answer
A
Question. The mapping f : N → N is given by f(n) = 1 + n2, n ∈ N when N is the set of natural numbers is
(a) one-one and onto
(b) onto but not one-one
(c) one-one but not onto
(d) neither one-one nor onto
Answer
C
Question. Let f : R → R be a function defined by f(x) = x3 + 4, then f is
(a) injective
(b) surjective
(c) bijective
(d) none of these
Answer
C
Question. Given set A ={1, 2, 3} and a relation R = {(1, 2), (2, 1)}, the relation R will be
(a) reflexive if (1, 1) is added
(b) symmetric if (2, 3) is added
(c) transitive if (1, 1) is added
(d) symmetric if (3, 2) is added
Answer
C
Question. Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x)=(x−2)/(x−3). Then,
(a) f is bijective
(b) f is one-one but not onto
(c) f is onto but not one-one
(d) None of these
Answer
A
Question. The relation R on the set A ={1,2,3} given by R = {(1,1), (1,2), (2,2), (2,3), (3,3)} is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Equivalence
Answer
A
Question. The function f : R → R given by f(x) = x3 – 1 is
(a) a one-one function
(b) an onto function
(c) a bijection
(d) neither one-one nor onto
Answer
C
Question. Which of the following functions from Z into Z are bijective?
(a) f(x) = x3
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f(x) = x2 + 1
Answer
B
Question. Let f: 𝑅 → 𝑅 be defined as f(x) =3x – 2. Choose the correct answer.
(a) f is one-one onto
(b) f is many one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Answer
A
Question. If N be the set of all-natural numbers, consider f : N → N such that f(x) = 2x, ∀ x ∈ N, then f is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d) None of these
Answer
B
Read Assertion and reason carefully and write correct option for each question
(a) Both A and R are correct; R is the correct explanation of A.
(b) Both A and R are correct; R is not the correct explanation of A.
(c) A is correct; R is incorrect.
(d) R is correct; A is incorrect.
Question. Assertion (A) if n (A) = p and n(B) = q The number of relation from set A to B is 𝑝𝑞
Reason (R) The number of subset of A X B is 2𝑝𝑞
Answer
D
Question. Assertion (A) The number of all one-one functions from set A = {1, 2, 3} to itself is 6
Reason (R) if n (A) = p and n(B) = q The number of function from set A to B is 𝑝𝑞
Answer
C
Question. Assertion= {(T1, T2) : T1 is congruent to T2}. Then R is an equivalence relation.
Reason(R)Any relation R is an equivalence relation, if it is reflexive, symmetric and transitive
Answer
A
Question. Assertion (A) Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. R is not equivalence relation.
Reason (R) R is not Reflexive relation but it is symmetric and transitive
Answer
C
Question. Assertion (A) the function f :N→N, given by f (1) = f (2) = 1 and f (x) = x – 1, for every x > 2, is onto but not one-one.
Reason (R) fis not one-one, as f (1) = f (2) = 1. But f is onto, as given any y ∈N, y ≠1, we can choose x as y + 1 such that f (y + 1) = y + 1 – 1 = y. Also for 1 ∈N, we have f (1) = 1.
Answer
A
Question. Assertion (A)Let L be the set of all lines in a plane and R be the relation in L defined as R = {(L1, L2) : L1 is perpendicular to L2}. R is not equivalence realtion.
Reason (R)R is symmetric but neither reflexive nor transitive
Answer
A
Question. Assertion (A) Let A and B be sets. Show that f : A × B →B × A such that f (a, b) = (b, a) is bijective function
Reason (R) f is said to equivalence relation if f is reflexive , symmetric and transitive
Answer
B
Question. Assertion (A) The function f :N→N, given by f (x) = 2x, is one-one
Reason (R) The function f is one-one, for f (x) = f (y) ⇒2x = 2y⇒x = y.
Answer
A
Question. Assertion (A) The relation R in R defined as R = {(a, b) :a≤𝑏2} is not equivalence relation.
Reason (R) Since R is not reflexive but it is symmetric and transitive.
Answer
A
Question. Assertion (A) The function f :N→N, given by f (x) = 2x, is not onto.
Reason (R) The function f is onto, for f (x) = f (y) ⇒2x = 2y⇒x = y.
Answer
C

We hope you liked the above provided MCQ Questions Chapter 1 Relations and Functions Class 12 Mathematics with solutions. If you have any questions please ask us in the comments box below.


