Atoms Class 12 Physics Important Questions

Please refer to Atoms Class 12 Physics Important Questions with solutions provided below. These questions and answers have been provided for Class 12 Physics based on the latest syllabus and examination guidelines issued by CBSE, NCERT, and KVS. Students should learn these problem solutions as it will help them to gain more marks in examinations. We have provided Important Questions for Class 12 Physics for all chapters in your book. These Board exam questions have been designed by expert teachers of Standard 12.

Class 12 Physics Important Questions Atoms

Very Short Answer Type Questions

Question. What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state ?
Answer. If n is the quantum number of highest energy level, then the total number of possible spectral lines emitted is

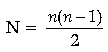
Here, third excited state means fourth energy level, i.e., n = 4

Question. What will be the ionisation potential if the first excitation potential of a given atom is 10.2 V?
Answer. The minimum energy needed to ionized an atom is called ionisation energy. The potential difference through which an electron should be accelerated to acquire energy is called ionisation potential.

Question. Which series of atomic spectrum of Hydrogen lies in infrared region?
Answer. Paschen series.

Question. What will be the radius of a Hydrogen atom when it is in first excited state?
Answer. The radius is given by
r₂ = r₁ (2)²
= 4r₁

Question. What are the drawbacks of Thomson’s model of atom.
Answer.

Question. Name the experiment responsible for the discovery of atomic nucleus.
Answer. Rutherford’s Alpha Scattering Experiment.

Question. Most of the mass of an atom is with the positive charge. In case of hydrogen atom, what fraction of the atomic mass is with the positive charge?
Answer. A hydrogen atom contains one proton (+ve charge) and one electron (–ve charge). As the mass of a proton is 1836 times that of an electron, so 1836/1837 part of the atomic mass is associated with the positive charge. 

Question. Out of the three radiations of the wavelength 8000 Angstrom, 5000 Angstrom and 1000 Angstrom, which one corresponds to Lyman series of Hydrogen spectrum. 
Answer. 1000 Angstrom; because it belongs to ultraviolet radiations in the electromagnetic spectrum.

Short Answer Type Questions-I

Question. Write the shortcomings of Rutherford atomic model. Explain how these were overcome by the postulates of Bohr’s atomic model.
Answer. Shortcomings of Rutherford atomic model:
Rutherford proposed planetary model of atom in which electrons revolve round the nucleus.
An electron revolving round the nucleus has an acceleration directed towards the nucleus.
Such accelerated electron must radiate electromagnetic radiation.
But, if an revolving electron radiates energy, the total energy of the system must decrease. In such situation, the electron must come closer to the nucleus and hit the nucleus. Also, the radiation spectrum of emitted electromagnetic waves should be continuous.
However, this does not happen in an atom. Atom is not unstable and the spectrum is not continuous.
Rutherford atomic model cannot explain these two observations. These are the shortcomings of Rutherford Atomic Model.
To overcome this discrepancy, Neils Bohr put forward three postulates combining classical Physics and Planck’s quantum hypothesis.
Bohr’s 1st postulate provides stability to the atomic model.
Bohr’s 2nd postulate provides justification that electrons may revolve in stationary orbit.
Bohr’s 3rd postulate provides the explanation of line spectrum.

Question. Calculate the ratio of the frequencies of the radiation emitted due to transition of the electron in a hydrogen atom from its (i) second permitted energy level to the first level and (ii) highest permitted energy level to the second permitted level.
Answer. Formulae ½
(i) Frequency of first case
(ii) Frequency of second case
Ratio
We have,

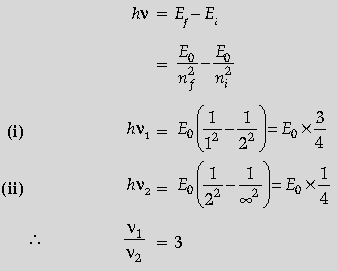
Question. A hydrogen atom in the ground state is excited by an electron beam of 12.5 eV energy. Find out the maximum number of lines emitted by the atom from its excited state.
Answer. Calculation of energy in excited state Formula
Finding out the maximum number of lines. 
Energy in ground state, E1 = –13.6 eV
Energy supplied = 12.5 eV
Energy in excited state, –13.6+ 12.5 = –l.l eV

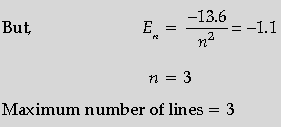
Question. Calculate the orbital period of the electron in the first excited state of hydrogen atom.
Answer. Statement of the Formula for r_n
Statement of the formula for v_n
Obtaining formula for T_n
Getting expression for T₂ (n = 2)

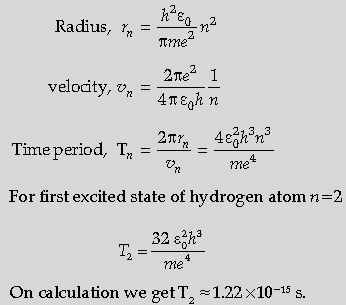
Alternatively,
If the student writes directly T_n ∝ n³
T₂ = 8 times of orbital period of the electron in the ground state (award one mark only)

Question. Use Bohr’s model of hydrogen atom to obtain the relationship between the angular momentum and the magnetic moment of revolving electron.
Answer. In Bohr model of Hydrogen atom, electron is modeled as a point negative charge rotating in a circular orbit about a fixed axis about a nucleus.

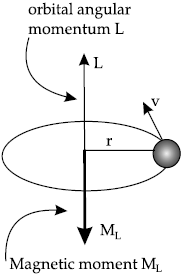
Let us consider
r = Radius of the orbit
v = Velocity
e = Charge of electron
m = Mass of electron

Question. The ground state energy of hydrogen atom is – 13.6 eV. If an electron makes a transition from an energy level – 1.51 eV to – 3.4 eV, calculate the wavelength of the spectral line emitted and the series of hydrogen spectrum to which it belongs.

Answer. Energy difference = 3.4 eV – 1.51 eV
= 1.89 eV = 3.024 × 10^–19 J

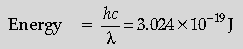
Wavelength = 6.47 × 10^–7 m
The given series is Balmer series.

Question. State Bohr’s quantization condition of angular momentum. Calculate the shortest wavelength of the Bracket series and state to which part of the electromagnetic spectrum does it belong.
Answer. Statement of Bohr’s quantization condition Calculation of shortest wavelength Identification of part of electromagnetic spectrum Electron revolves around the nucleus
only in those orbits for which the angular momentum is some integral of h/2π. (where h is Planck’s constant) Also give full credit if a student write mathematically

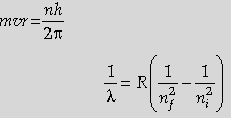
For Brackett Series,
Shortest wavelength is for the transition of electrons from n_i = ∞ to n_f = 4

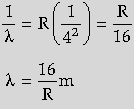
= 1458.5 nm on substitution of value of R Infrared region.
[Note: Don’t deduct any mark for this part, when a student does not substitute the value of R, to calculate the numerical value of λ ]

Question. Write two important limitations of Rutherford’s nuclear model of the atom.
Answer. (i) According to Rutherford’s model, electron orbiting around the nucleus, continuously radiates energy due to the acceleration; hence the atom will not remain stable.
(ii) As electron spirals inwards; its angular velocity and frequency change continuously; therefore it will emit a continuous spectrum.

Question. Define the distance of closest approach. An a-particle of kinetic energy ‘K’ is bombarded on a thin gold foil. The distance of the closest approach is ‘r’. What will be the distance of closest approach for an a- particle of double the kinetic energy ?
Answer. It is the distance of charged particle from the centre of the nucleus, at which the whole of the initial kinetic energy of the (far off) charged particle gets converted into the electric potential energy of the system.
Distance of closest approach (rc) is given by

[Alternatively: If a candidate writes directly r/2 without mentioning formula, award the 1 mark for this part.]

Question. Show that the radius of the orbit in hydrogen atom varies as n², where n is the principal quantum number of the atom.
Answer.

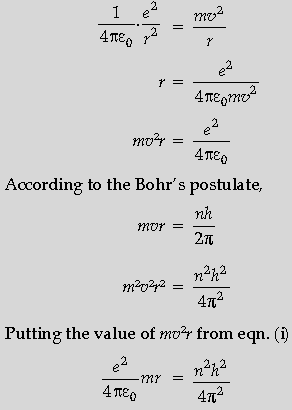
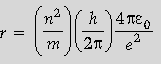
The above equation shows that r is directly proportional to n²

Question. Calculate the de-Broglie wavelength of the electron orbiting in the n = 2 state of hydrogen atom. 
Answer. Formulae of kinetic energy and de-Broglie a wavelength 
Calculation and Result
Kinetic energy for the second state-

Question. The short wavelength limit for the Lyman series of the hydrogen spectrum is 913·4 Å. Calculate the short wavelength limit for Balmer series of the hydrogen spectrum. 
Answer. Formula
Calculation

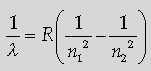
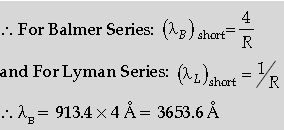
Question. Calculate the shortest wavelength of the spectral lines emitted in Balmer series.
[Given Rydberg constant, R = 10⁷ m^–1]
Answer. Formula
Calculation and Result

Question. In the ground state of hydrogen atom, its Bohr radius is given as 5.3 × 10^–11 m. The atom is excited such that the radius becomes 21.2 × 10^–11 m. Find (i) the value of the principal quantum number and (ii) the total energy of the atom in this excited state.
Answer. (i) r = r₀n²
21.2 × 10^–11 = 5.3 × 10^–11 n²
⇒ n = 2

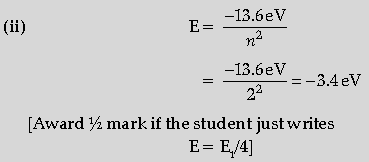
Question. The energy levels of a hypothetical atom are given below. Which of the shown transitions will result in the emission of photon of wavelength 275 nm ?

Answer. (i) Energy of photon =hc/λ

Short Answer Type Questions-II

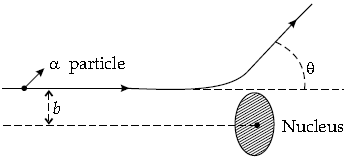
Question. (a) Explain briefly how Rutherford scattering of α-particle by a target nucleus can provide information on the size of nucleus.
(b) Show that density of nucleus is independent of its mass number A.
Answer. (a) Explanation of information on the size of nucleus
(b) Showing the independence of density on mass number
(a) Many of the α-particles pass through the foil. A few particles deflect by more than 90° angle. Rutherford argued that to deflect the α-particles backward, it must experience a large repulsive force. It shows that most of the part of an atom is the empty space and its positive charge is concentrated tightly at its centre and its size is very small as compared to the size of atom.

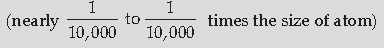
Alternatively,
In Rutherford experiment, the calculation of distance of closest approach provides information about the size of the nucleus.
Let K be the initial kinetic energy of the alpha particle. At the distance of closest approach

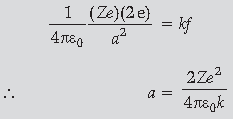
(b) Radius of the nucleus of mass number A,
R = R0A^1/3, where, R₀ is constant.
Volume of the nucleus,

Question. (a) How is the stability of hydrogen atom in Bohr model explained by de-Broglie’s hypothesis ?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to n = 4 level.
When it gets de-excited, find the maximum number of lines which are emitted by the atom. Identify the series to which these lines belong. Which of them has the shortest wavelength ?
Answer. (a) Explanation 
(b) Identification of Series 
(c) Identification of shortest wavelength
(a) Explanation: The quantised electron orbits and energy state are due to wave nature of the electron and only resonant standing waves can persist.
According to de Broglie Hypothesis,

(b) Lyman series:
transition from n = 4 to n = 1 will have shortest wavelength

Question. Derive an expression for the frequency of radiation emitted when a hydrogen atom de -excites from level n to level (n – 1). Also show that for large values of n, this frequency equals to classical frequency of revolution of an electron.
Answer. Derivation of frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n – 1).

Question. Draw a plot of a-particle scattering by a thin foil of gold to show the variation of the number of the scattered particles with scattering angle. Describe briefly how the large angle scattering explains the existence of the nucleus inside the atom. Explain with the help of impact parameter picture, how Rutherford scattering serves a powerful way to determine an upper limit on the size of the nucleus.
Answer. Draw a plot of a-particle scattering to show variation of scattering particle.
Describe briefly how large scattering explains existence of nucleus.
Explain with the help of impact parameter picture how Rutherford scattering serves powerful way to determine upper limit of nucleus.

The data shows that large number of a-particles do not suffer large scattering but small number suffer greater scattering. It is concluded that 
(i) most of the space in the atom is empty.
(ii) massive positively charged nucleus occupies small region.

From the picture, it is clear that small impact parameter suffers large scattering, thus it shows the upper limit to the size of nucleus.

Question. (a) State Bohr’s postulate to define stable orbits in hydrogen atom. How does de Broglie’s hypothesis explain the stability of these orbits?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 level. Estimate the frequency of the photon.
Answer. (a) Statement of Bohr’s postulate 
Explanation in terms of de Broglie hypothesis
(b) Finding the energy in the n = 4 level Estimating the frequency of the photon 
(a) Bohr’s postulate, for stable orbits, states “The electron, in an atom, revolves around the nucleus only in those orbits for which its angular momentum is an integral multiple

Thus de –Broglie showed that formation of stationary pattern for integral ‘n’ gives rise to stability of the atom.
This is nothing but the Bohr’s postulate

Question. Using Bohr’s postulates, derive the expression for the orbital period of the electron moving in the n^th orbit of hydrogen atom.
Answer.

(Also accept if the student calculates T by obtaining expressions for both v and r.)

Question. (i) State Bohr’s quantization condition for defining stationary orbits. How does de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between the three wavelengths λ₁, λ₂ and λ₃ from the energy level diagram shown below.

Answer. (i) Statement of Bohr’s quantization condition de- Broglie explanation of stationary orbits 
(ii) Relation between λ₁, λ₂ λ₃
(i) Only those orbits are stable for which the angular momentum, of revolving electron, is an integral
multiple of h/2π
Alternatively

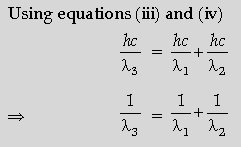
Question. Find the ratio between the wavelengths of the ‘most energetic’ spectral lines in the Balmer and Paschen series of the hydrogen spectrum.
Answer. Spectral lines in Balmer series,

Long Answer Type Questions

Question. (a) State the postulates of Bohr’s model of hydrogen atom and derive the expression for Bohr radius.
(b) Find the ratio of the longest and the shortest wavelengths amongst the spectral lines of Balmer series in the spectrum of hydrogen atom.

Answer. (a) Postulates of Bohr Model of Hydrogen atom:
Postulate – I: The electrons revolve in a circular orbit around the nucleus. The electrostatic force of attraction between the positively charged nucleus and negatively charged electrons provide necessary centripetal force for circular motion.
Postulate – II: The electrons can revolve only in certain selected orbits in which angular momentum of electrons is equal to the integral multiple h/2p where h is Planck’s constant. These orbits are known as stationary or permissible orbits. The electrons do not radiate energy while revolving in theses orbits.
Postulate – III: When an electrons jumps from higher energy orbit to lower energy orbit, energy is radiated in the form of a quantum or photon of energy hv, which is equal to the difference of the energies of the electron in the two orbits.
Expression for Bohr radius:
Let us consider
m = Mass of an electron
r = Radius of the circular orbit in which the
electron is revolving
v = Speed of electron
– e = Charge of electron
From 1^st postulate
Centripetal force = Electrostatic force

Question. (i) Using Bohr’s postulates, derive the expression for the total energy of the electron in the stationary states of the hydrogen atom.
(ii) Using Rydberg formula, calculate the wavelengths of the spectral lines of the first member of the Lyman series and of the Balmer series.
Answer. (i)

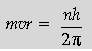
Question. (i) In Rutherford scattering experiment, draw the trajectory traced by a-particles in the coulomb field of target nucleus and explain how this led to estimate the size of the nucleus.
(ii) Describe briefly how wave nature of moving electrons was established experimentally.
(iii) Estimate the ratio of de-Broglie wavelengths associated with deuterons and a-particles when they are accelerated from rest through the same accelerating potential V. 
Answer. (i) The trajectory, traced by the a-particles in the Coulomb field of target nucleus, has the form as shown below:

The size of the nucleus was estimated by observing the distance (d) of closest approach, of the a-particles. This distance is given by:

where, K = kinetic energy of the a-particles when they are far away from the target nuclei.
(ii) The wave nature of moving electrons was established through the Davisson-Germer experiment.
In this experiment, it was observed that a beam of electrons, when scattered by a nickel target, showed ‘maxima’ in certain directions; (like the ‘maxima’ observed in interference/diffraction experiments with light.)