Please refer to Assignments Class 11 Mathematics Straight Lines Chapter 10 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 10 Straight Lines Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Straight Lines Assignments Class 11 Mathematics
Question. Which of the following lines is farthest from the origin?
(a) x – y + 1 = 0
(b) 2x – y + 3 = 0
(c) x + 2y – 2 = 0
(d) x + y – 2 = 0
Answer
D
Question. If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through
(a) (1, – 2)
(b) (1, 2)
(c) (– 1, 2)
(d) (– 1, – 2)
Answer
A
Question. If the points ( x, y), (1, 2) and ( –3, 4) are collinear, then
(a) x + 2y – 5 = 0
(b) x + y – 1 = 0
(c) 2x + y – 4 = 0
(d) 2x – y + 10 = 0
Answer
A
Question. The equation of two equal sides of an isosceles triangle are 7x – y + 3 = 0 and x + y – 3 = 0 and its third side passes through the point (1, – 10), then the equation of the third side is (are)
(a) 3x + y + 7 = 0, x – 3y – 31 = 0
(b) 2x + y + 5 = 0, x – 2y + 3 = 0
(c) 3x + y + 7 = 0, x + y = 0
(d) 3x – y = 7, x + 3y = 15
Answer
A
Question. The lines x + 2y – 5 = 0, 2x – 3y + 4 = 0, 6x + 4y – 13 = 0
(a) are concurrent.
(b) form a right angled triangle.
(c) form an isosceles triangle.
(d) form an equilateral triangle.
Answer
B
Question. The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is given by :

Answer
A
Question. The equations of the lines which cuts off an intercept –1 from y-axis and equally inclined to the axes are
(a) x – y + 1 = 0, x + y + 1 = 0
(b) x – y – 1 = 0, x + y – 1 = 0
(c) x – y – 1 = 0, x + y + 1 = 0
(d) None of these
Answer
C
Question. A straight line makes an angle of 135° with x-axis and cuts y-axis at a distance of – 5 from the origin. The equation of the line is
(a) 2x + y + 5 = 0
(b) x + y + 5 = 0
(c) x + 2y + 3 = 0
(d) x + y + 3 = 0
Answer
B
Question. Slope of a line which cuts off intercepts of equal lengths on the axes is
(a) 2
(b) 0
(c) –1
(d) 3
Answer
C
Question. What is the angle between the two straight lines y = (2 − √3)x + 5 and y = (2 + √3) x − 7?
(a) 60°
(b) 45°
(c) 30°
(d) 15°
Answer
A
Question. The value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear, is
(a) 4
(b) 2
(c) 3
(d) 1
Answer
D
Question. If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2) then the equation of the line will be
(a) 2x + 3y = 12
(b) 3x + 2y = 12
(c) 4x – 3y = 6
(d) 5x – 2y = 10
Answer
A
Question. Slope of non-vertical line passing through the points (x1, y1) and (x2, y2) is given by :
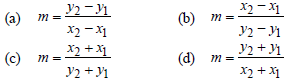
Answer
A
Question. The values of k for which the line (k – 3) x – (4 – k2)y + k2 – 7k + 6 = 0 is parallel to the x-axis, is
(a) 3
(b) 2
(c) 1
(d) 4
Answer
A
Question. If a line makes an angle α in anti-clockwise direction with the positive direction of x-axis, then the slope of the line is given by :
(a) m = sin α
(b) m = cos α
(c) m = tan α
(d) m = sec α
Answer
C
Question. The bisector of the acute angle formed between the lines 4x – 3y + 7 = 0 and 3x – 4y + 14 = 0 has the equation
(a) x + y +3 = 0
(b) x – y – 3 = 0
(c) x – y + 3 = 0
(d) 3x + y – 7 = 0
Answer
C
Question. In what ratio does the line y – x + 2 = 0 cut the line joining (3, –1) and ( 8, 9)?
(a) 2 : 3
(b) 3 : 2
(c) 3 : –2
(d) 1 : 2
Answer
A
Question. The tangent of angle between the lines whose intercepts on the axes are a, –b and b, –a respectively, is
(a) a2 – b2/ab
(b) b2 – a2/2
(c) b2 – a2/2ab
(d) None of these
Answer
C
Question. What is the value of y so that the line through (3, y) and (2, 7) is parallel to the line through (– 1, 4) and (0, 6)?
(a) 6
(b) 7
(c) 5
(d) 9
Answer
D
Question. The equation of the straight line that passes through the point (3, 4) and perpendicular to the line 3x + 2y + 5 = 0 is
(a) 2x + 3y + 6 = 0
(b) 2x – 3y – 6 = 0
(c) 2x – 3y + 6 = 0
(d) 2x + 3y – 6 = 0
Answer
C
Question. The equation of a straight line which cuts off an intercept of 5 units on negative direction of y-axis and makes an angle of 120º with the positive direction of x-axis is
(a) √3x + y + 5 = 0
(b) √3x + y − 5 = 0
(c) √3x − y − 5 = 0
(d) √3x − y + 5 = 0
Answer
A
Question. Line through the points (–2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
(a) 2
(b) 3
(c) 4
(d) 5
Answer
C
Question. If A and B are two points on the line 3x + 4y + 15 = 0 such that OA = OB = 9 units, then the area of the triangle OAB is
(a) 18 sq. units
(b) 18√2 sq. units
(c) 18/√2 sq. units
(d) None of these
Answer
B
Question. The length of the perpendicular from the origin to a line is 7 and line makes an angle of 150° with the positive direction of y-axis then the equation of the line is
(a) 4x + 5y = 7
(b) –x + 3y = 2
(c) √3x − y = 10√2
(d) √3x + y = 14
Answer
D
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. The length of perpendicular from a given point (x1, y1) to a line ax + by + c = 0 is
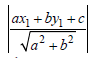
II. Three or more straight lines are said to be concurrent lines, if they meet at a point.
Choose the correct option
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
C
Question. Consider the following statements.
I. The equation of a straight line passing through the point (x1, y1) and having slope m is given by
y – y1 = m(x – x1)
II. Equation of the y-axis is x = 0.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false.
Answer
C
Question. Consider the following statements.
I. Two lines are parallel if and only if their slopes are equal.
II. Two lines are perpendicular if and only if product of their slopes is 1.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false.
Answer
A
Question. Consider the following statements.
I. The equation of a straight line making intercepts a and b on x and y-axis respectively is given by
x/a + y/b = 1
II. If ax + by + c1 = 0 and ax + by + c2 = 0 be two parallel lines, then distance between two parallel lines, d = lc1 – c2/√a2 + b2l.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
C
Question. Consider the following statements.
I. Equation of the line passing through (0, 0) with slope m is y = mx
II. Equation of the x-axis is x = 0.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
A
Question. Consider the following statements.
I. Centroid of a triangle is a point where angle bisectors meet.
II. If value of area after calculations is negative then we take its negative value.
Choose the correct option
(a) Only I is false
(b) Only II is false
(c) Both are false
(d) Both are true
Answer
C
Question. Consider the equation √3x + y−8 =0
I. Normal form of the given equation is cos 30°x + sin 30° y = 4
II. Values of p and w are 4 and 30° respectively.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
C
Question. Consider the following statements.
I. Slope of horizontal line is zero and slope of vertical line is undefined.
II. Two lines whose slopes are m1 and m2 are perpendicular if and only if m1m2 = –1
Choose the correct option.
(a) Both are true
(b) Both are false
(c) Only I is true
(d) Only II is true
Answer
A
Question. If the point (x, y) be equidistant from the points
(a + b,b − a) and (a − b,a + b) , then:
(a) ax + by = 0
(b) ax − by = 0
(c) bx + ay = 0
(d) bx − ay = 0
Answer
D
Question. The equation of the bisector of the acute angle between the lines 3x − 4y + 7 = 0 and 12x + 5y − 2 = 0 is:
(a) 21x + 77 y −101 = 0
(b) 11x − 3y + 9 = 0
(c) 31x + 77 y +101 = 0
(d) 11x − 3y − 9 = 0
Answer
B
Question. If the length of the perpendicular drawn from origin to the line whose intercepts on the axes are a and b be p, then
(a) a2 + b2 = p2
(b) a2 + b2 = 1/p2
(c) 1/a2 + 1/b2 = 2/p2
(d) 1/a2 + 1/b2 = 1/p2
Answer
D
Question. If cartesian co-ordinates of any point are (√3,1) , then its polar co-ordinates is:
(a) (√2,π / 3)
(b) ( 2,π / 6)
(c) (2,π/6)
(d) None of these
Answer
C
Question. ABC is an isosceles triangle. If the co-ordinates of the base are B(1,3) and C (– 2,7) the co-ordinates of vertex A can be:
(a) (1, 6)
(b) (–1/2,5)
(c) (5/6,6)
(d) None of these
Answer
C
Question. The line joining points (2,–3) and (–5, 6)is divided by yaxis in the ratio:
(a) 2 : 5
(b) 2 : 3
(c) 3 : 5
(d) 1 : 2
Answer
A
Question. The incentre of the triangle with vertices (1, 3), (0,0) and (2, 0) is:
(a) (1,√3/2)
(b) (2/3,1/√3)
(c) (2/3,√3/2)
(d) (1,1/√3)
Answer
D
Question. The vertices of triangle are (0, 3) (– 3, 0) and (3, 0). The co-ordinate of its orthocentre are:
(a) (0, – 2)
(b) (0, 2)
(c) (0, 3)
(d) (0, –3)
Answer
C
Question. The area of the triangle formed by the points (a,b + c),(b,c + a), (c,a + b) is:
(a) abc
(b) a2 + b2 + c2
(c) ab + bc + ca
(d) 0
Answer
D
Question. Three lines px + qy + r = 0,qx + ry + p = 0 and rx + py +q = 0 are concurrent, if:
(a) p + q + r = 0
(b) b2 + q2 + r2 = pr + rq
(c) p3 + q3 + r3 = 3pqr
(d) None of the above
Answer
A,C
Question. All points lying inside the triangle formed by the points (1, 3), (5, 0) and (–1, 2) satisfy:
(a) 3x + 2y ≥ 0
(b) 2x + y – 13 ≥ 0
(c) 2x – 3y – 12 ≤ 0
(d) – 2x + y ≥ 0
Answer
A,C
Question. Three points are A(6, 3), B(– 3, 5), C(4, – 2) and P (x, y) is a point, then the ratio of area of △PBC and △ABC is:
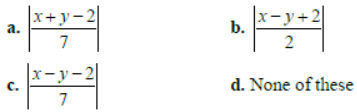
Answer
A
Question. The points (1, 1); 2 2 (0, sec θ ); (cosec θ ,0) are collinear for:
(a) θ = nπ / 2
(b) θ ≠ nπ / 2
(c) θ = nπ
(d) None of these
Answer
B
Question. The equation (b−c)x+(c−a)y+a−b = 0,(b3 −c3 )x +(c3 −a3 ) y + a3 − b3 = 0 will represent the same line if:
(a) b = c
(b) c = a
(c) a = b
(d) a + b +c = 0
Answer
ALL
Question. Consider the straight lines x+2y+4= 0 and 4x + 2y –1 = 0. The line 6x + 6y +7 = 0 is:
(a) bisector of the angle including origin
(b) bisector of acute angle
(c) bisector of obtuse angle
(d) none of the above
Answer
A,B
Question. The points (0, 8/3) (1, 3) and (82, 30) are the vertices of:
(a) An equilateral triangle
(b) An isosceles triangle
(c) A right angled triangle
(d) None of these
Answer
D
Question. The point (2,3) undergoes the following three transformation successively,
(a) Reflection about the line y = x .
(b) Transformation through a distance 2 units along the positive direction of y-axis.
(c) Rotation through an angle of 45o about the origin in the anticlockwise direction. The final coordinates of points are
(a) (1,√2/7,√2)
(b) (–1,√2/7,√2)
(c) (1,√2/–7,√2)
(d) None of these
Answer
B
Question. Let PS be the median of the triangle with vertices P(2,2),Q(6,−1) and R(7, 3). The equation of the line passing through (1, – 1) and parallel to PS is:
(a) 2x − 9 y − 7 = 0
(b) 2x − 9 y −11 = 0
(c) 2x + 9y −11 = 0
(d) 2x + 9y + 7 = 0
Answer
D
Question. The equation of the line passes through (a, b) and parallel to the line x/a + y/b =1 ,is
(a) x/a + y/b =3
(b) x/a + y/b =2
(c) x/a + y/b =0
(d) x/a + y/b + 2 = 0
Answer
B
Question. A line passes through (2, 2) and is perpendicular to the line 3x + y = 3 . Its y-intercept is:
(a) 1/3
(b) 2/3
(c) 1
(d) 4/3
Answer
D
Question. If we reduce 3x + 3y + 7 = 0 to the form xcosα + y sin α = p , then the value of p is:
(a) 7/2√3
(b) 7/3
(c) 3√7/2
(d) 7/3√2
Answer
D
Question. The equation of straight line passing through point of intersection of the straight lines 3x − y + 2 = 0 and 5x − 2y + 7 = 0 and having infinite slope is:
(a) x = 2
(b) x + y = 3
(c) x = 3
(d) x = 4
Answer
C
Question. Angle between the lines 2x − y −15 = 0 and 3x + y + 4 = 0 is:
(a) 90°
(b) 45°
(c) 180°
(d) 60°
Answer
B
Question. To which of the following types the straight lines represented by 2x + 3y − 7 = 0 and 2x + 3y − 5 = 0 belongs:
(a) Parallel to each other
(b) Perpendicular to each other
(c) Inclined at 45° to each other
(d) Coincident pair of straight lines
Answer
A
Question. The equation of the lines which passes through the point (3,–2) and are inclined at 60º to the line 3x + y =1?
(a) y + 2 = 0, √3x − y − 2 − 3√3 = 0
(b) x − 2 = 0, √3x − y + 2 + 3√3 = 0
(c) √3x − y − 2 − 3√3 = 0
(d) None of these
Answer
A
Question. If the lines y = 3x +1 and 2y = x + 3 are equally inclined to the line y = mx + 4 , then m = ?
(a) 1+3√2/7
(b) 1–3√2/7
(c) 1+3√2/7
(d) 1+5√2/7
Answer
D
Question. The angle between the lines whose intercepts on the axes are a, – b and b, – a respectively, is:
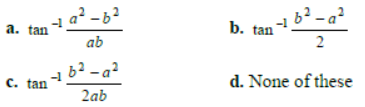
Answer
C
Question. A straight line (√3 −1)x = (√3 +1) y makes an angle 75° with another straight line which passes through origin. Then the equation of the line is:
(a) x = 0
(b) y = 0
(c) x + y = 0
(d) x − y = 0
Answer
A
Question. The inclination of the straight line passing through the point (–3, 6) and the midpoint of the line joining the point (4, –5) and (–2, 9) is:
(a) π / 4
(b) π / 6
(c) π /3
(d) 3π / 4
Answer
D
Question. The angle between the straight lines x − y√3 = 5 and √3x + y = 7 is:
(a) 90°
(b) 60°
(c) 75°
(d) 30°
Answer
A
