Please refer to Assignments Class 11 Mathematics Sets Chapter 1 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 1 Sets Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Sets Assignments Class 11 Mathematics
Question. Let S = {1, 2, 3, … , 100}. The number of non-empty subsets A of S such that the product of elements in A is even is :
(a) 2100 -1
(b) 250 (250-1)
(c) 250 – 1
(d) 250 + 1
Answer
B
Question. Let Z be the set of integers. If A = {x ∈ Z : 2(x + 2) ( x2 – 5x + 6) = 1} and B = {x ∈ Z : –3 < 2x – 1< 9}, then the number of subsets of the set A × B, is :
(a) 215
(b) 218
(c) 212
(d) 210
Answer
A
Question. If f(x) + 2f (1/x) = 3x, x ≠ 0 and S = {x ∈ R : f(x) = f(–x)}; then S:
(a) contains exactly two elements.
(b) contains more than two elements.
(c) is an empty set.
(d) contains exactly one element.
Answer
A
Question. Two newspapers A and B are published in a city. It is known that 25% of the city population reads A and 20% reads B while 8% reads both A and B. Further, 30% of those who read A but not B look into advertisements and 40% of those who read B but not A also look into advertisements, while 50% of those who read both A and B look into advertisements. Then the percentage of the population who look into advertisements is:
(a) 13.9
(b) 12.8
(c) 13
(d) 13.5
Answer
A
Question. Let X ={1,2,3,4,5}. The number of different ordered pairs (Y, Z) that can formed such that Y ⊄ X, Z ⊄ X and Y ∩ Z is empty is :
(a) 52
(b) 35
(c) 25
(d) 53
Answer
B
Question. In a certain town, 25% of the families own a phone and 15% own a car; 65% families own neither a phone nor a car and 2,000 families own both a car and a phone. Consider the following three statements :
(A) 5% families own both a car and a phone
(B) 35% families own either a car or a phone
(C) 40,000 families live in the town
Then,
(a) Only (A) and (C) are correct.
(b) Only (B) and (C) are correct.
(c) All (A), (B) and (C) are correct.
(d) Only (A) and (B) are correct.
Answer
C
Question. Let P = {θ : sinθ – cosθ = √2 cosθ} and θ = {θ : sinθ + cosθ = √2 sinθ} be two sets. Then:
(a) P ⊂ Q and Q- P ≠ φ
(b) Q ⊄ P
(c) P = Q
(d) P ⊄ Q
Answer
C
Question. Set A has m elements and set B has n elements. If the total number of subsets of A is 112 more than the total number of subsets of B, then the value of m×n is ______.
Answer
28
Question. A relation on the set A = {x : |x| < 3, x ∈ Z}, where Z is the set of integers is defined by R = {(x, y) : y = |x|, x ≠ – 1}. Then the number of elements in the power set of R is:
(a) 32
(b) 16
(c) 8
(d) 64
Answer
B
Question. Let S = {x ∈ R : x ≥ 0 and 2 | √x – 3| + √x( √x – 6) + 6 = 0 . Then S :
(a) contains exactly one element.
(b) contains exactly two elements.
(c) contains exactly four elements.
(d) is an empty set.
Answer
B
Question. A survey shows that 73% of the persons working in an office like coffee, whereas 65% like tea. If x denotes the percentage of them, who like both coffee and tea, then x cannot be :
(a) 63
(b) 36
(c) 54
(d) 38
Answer
B
Question. Let X = {n ∈ N: l ≤ n ≤ 50}. If
A = {n ∈ X: n is a multiple of 2} and
B = {n ∈ X: n is a multiple of 7}, then the number of elements in the smallest subset of X containing both A and B is __________.
Answer
29
Question. In a class of 140 students numbered 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is:
(a) 102
(b) 42
(c) 1
(d) 38
Answer
D
Question. A survey shows that 63% of the people in a city read newspaper A whereas 76% read newspaper B. If x% of the people read both the newspapers, then a possible value of x can be :
(a) 29
(b) 37
(c) 65
(d) 55
Answer
D
Question. If A, B and C are three sets such that A ∩ B= A ∩ C and A ∪ B = A ∪ C , then
(a) A = C
(b) B = C
(c) A ∩ B = φ
(d) A = B
Answer
B
Question. Let
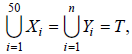
where each Xi contains 10 elements and each Yi contains 5 elements. If each element of the set T is an element of exactly 20 of sets Xi‘s and exactly 6 of sets Yi‘s, then n is equal to
(a) 15
(b) 50
(c) 45
(d) 30
Answer
D
Question. Let A, B and C be sets such that φ ≠ A ∩ B ⊄ C . Then which of the following statements is not true ?
(a) B ∩ C ≠ φ
(b) If (A- B) ⊄ C , then A ⊄ C
(c) (C ∪ A) ∩ (C ∪ B) = C
(d) If (A-C) ⊄ B , then A ⊄ B
Answer
D
