Please refer to Assignments Class 11 Mathematics Conic Sections Chapter 11 with solved questions and answers. We have provided Class 11 Mathematics Assignments for all chapters on our website. These problems and solutions for Chapter 11 Conic Sections Class 11 Mathematics have been prepared as per the latest syllabus and books issued for the current academic year. Learn these solved important questions to get more marks in your class tests and examinations.
Conic Sections Assignments Class 11 Mathematics
Question. If the line x + y = 1 is a tangent to a circle with centre (2, 3), then its equation is
(a) x2 + y2 + 2x + 2y + 5 = 0
(b) x2 + y2 – 4x – 6y + 5 = 0
(c) x2 + y2 – x – y + 3 = 0
(d) x2 + y2 + 5x + 2y = 0
Answer
B
Question. Equation of the ellipse whose axes are along the coordinate axes, vertices are (± 5, 0) and foci at (± 4, 0) is
(a) x2/16 + y2 /9 = 1
(b) x2/25 + y2 /9 = 1
(c) x2/4 + y2/25 = 1
(d) x2/25 + y2 /16 = 1
Answer
B
Question. For the parabola y2 = 8x, the length of the latus-rectum is
(a) 4
(b) 2
(c) 8
(d) None of these
Answer
C
Question. The cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100 m long is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Then, the length of supporting wire attached to the roadway 18 m from the middle is
(a) 10.02 m
(b) 9.11 m
(c) 10.76 m
(d) 12.06 m
Answer
B
Question. Equation of the circle passing through the origin and through the points of intersection of the circle x2 + y2 – 2x + 4y – 20 = 0 and the line x + y – 1 = 0 is
(a) x2 + y2 − 20x +15y = 0
(b) x2 + y2 + 33x + 33y = 0
(c) x2 + y2 – 22x –16y = 0
(d) 2x2 + 2y2 – 4x – 5y = 0
Answer
C
Question. If the straight line ax + by = 2 ; a, b ?? 0 touches the circle x2 + y2 – 2x = 3 and is normal to the circle x2 + y2 – 4y = 6, then the values of a and b are
(a) 3/2, 2
(b) −4/3, 1
(c) 1/4 , 2
(d) 2/3 , –1
Answer
B
Question. The equation of the parabola with vertex at origin, which passes through the point (–3, 7) and axis along the x-axis is
(a) y2 = 49x
(b) 3y2 = – 49x
(c) 3y2 = 49x
(d) x2 = – 49y
Answer
B
Question. The foci of the ellipse 25 (x + 1)2 + 9(y + 2)2 = 225 are at :
(a) (–1, 2) and (–1, –6)
(b) (–2, 1) and (–2, 6)
(c) (–1, –2) and (–2, –1)
(d) (–1, –2) and (–1, –6)
Answer
A
Question. The length of the transverse axis along x-axis with centre at origin of a hyperbola is 7 and it passes through the point (5, – 2). Then, the equation of the hyperbola is
(a) 4/49x2 − 196/51 y2 = 1
(b) 49/4x2 − 51/196 y2 = 1
(c) 4/49x2 − 51/196 y2 = 1
(d) None of these
Answer
C
Question. A pair of tangents are drawn from the origin to the circle x2 + y2 + 20 (x + y) + 20 = 0, then the equation of the pair of tangent are
(a) x2 + y2 − 5xy = 0
(b) x2 + y2 + 2x + y = 0
(c) x2 + y2 – xy + 7 = 0
(d) 2x2 + 2y2 + 5xy = 0
Answer
D
Question. The conic represented by x = 2 (cos t + sin t), y = 5 (cos t – sin t) is
(a) a circle
(b) a parabola
(c) an ellipse
(d) a hyperbola
Answer
C
Question. The sum of the minimum distance and the maximum distance from the point (4, – 3) to the circle x2 + y2 + 4x – 10y – 7 = 0 is
(a) 20
(b) 12
(c) 10
(d) 16
Answer
A
Question. In an ellipse, the distance between its foci is 6 and minor axis is 8. Then its eccentricity is
(a) 3/5
(b) 1/2
(c) 4/5
(d) 1/5
Answer
A
Question. The equations of the lines joining the vertex of the parabola y2 = 6x to the points on it which have abscissa 24 are
(a) y ± 2x = 0
(b) 2y ± x = 0
(c) x ± 2y = 0
(d) 2x ± y = 0
Answer
B
Question. A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at
(a) (0, 2)
(b) (1, 0)
(c) (0, 1)
(d) (2, 0)
Answer
B
Question. What is the difference of the focal distances of any point on the hyperbola?
(a) Eccentricity
(b) Distance between foci
(c) Length of transverse axis
(d) Length of semi-transverse axis
Answer
C
Question. A bar of given length moves with its extremities on two fixed straight lines at right angles. Any point of the bar describes

(a) parabola
(b) ellipse
(c) hyperbola
(d) circle
Answer
B
Question. A man running a race course notes that sum of its distance from two flag posts from him is always 10 m and the distance between the flag posts is 8 m. Then, the equation of the posts traced by the man is
(a) x2/25 + y2/9 = 1
(b) x2 + y2 = 25
(c) x2+ y2 = 9
(d) x2/9 + y2/25 = 1
Answer
A
Question. The latus rectum of the parabola y2 = 4ax whose focal chord is PSQ such that SP = 3 and SQ = 2 is given by :
(a) 24/5
(b) 12/5
(c) 6/5
(d) 1/5
Answer
A
Question. The equation of an ellipse with foci on the x-axis is
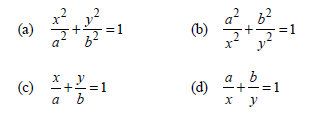
Answer
A
Question. The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation:
(a) x2 – 6x – 10y + 14 = 0
(b) x2– 10x – 6y + 14 = 0
(c) y2 – 6x – 10y + 14 = 0
(d) y2 – 10x – 6y + 14 = 0
Answer
D
Question. The equation of the conic with focus at (1, – 1) directrix along x – y + 1 = 0 and with eccentricity √2 is
(a) x2 – y2 = 1
(b) xy = 1
(c) 2xy – 4x + 4y + 1 = 0
(d) 2xy + 4x – 4y – 1 = 0
Answer
C
Question. Find the equation of a circle which passes through the origin and makes intercepts 2 units and 4 units on x-axis and y-axis respectively.
(a) x2 + y2 – 2x – 4y = 0
(b) x2 + y2 – 4y = 0
(c) x2 + y2 + 2x = 0
(d) x2 + y2 – 4x – 2y = 0
Answer
A
Question. For the ellipse 3x2 + 4y2 = 12 length of the latus rectum is:
(a) 3
(b) 4
(c) 3/5
(d) 2/5
Answer
A
Question. Eccentricity of ellipse x2/a2 + y2/b2 = 1 , if it passes through point (9, 5) and (12, 4) is
(a) √3/ 4
(b) √4 / 5
(c) √5 / 6
(d) √6/ 7
Answer
D
Question. A variable circle passes through the fixed point A( p,q) and touches x-axis . The locus of the other end of the diameter through A is
(a) ( y − q)2 = 4px
(b) (x − q)2 = 4py
(c) ( y − p)2 = 4qx
(d) (x − p)2 = 4qy
Answer
D
Question. A circle of radius 5 touches another circle x2 + y2 –2x – 4y – 20 = 0 at (5, 5) then its equation is :
(a) x2 + y2 + 18x + 16y + 120 = 0
(b) x2 + y2 – 18x – 16y + 120 = 0
(c) x2 + y2 – 18x + 16y + 120 = 0
(d) None of these
Answer
B
Question. The equation of parabola whose vertex (0, 0) and focus (3, 0) is y2 = 4ax. The value of ‘a’ is
(a) 2
(b) 3
(c) 4
(d) 1
Answer
B
Question. Angle between the tangents to the curve y = x2 − 5x + 6 at the points (2, 0) and (3, 0) is
(a) π
(b) π/2
(c) π/6
(d) π/4
Answer
B
Question. A.M. of the slopes of two tangents which can be drawn from the point (3, 1) to the circle x2 + y2 = 4 is
(a) 2/5
(b) 3/4
(c) 3/5
(d) 1/7
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
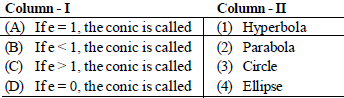
Codes
A B C D
(a) 2 1 4 3
(b) 2 4 1 3
(c) 3 1 4 2
(d) 3 4 1 2
Answer
B
Question. The vertex of the parabola (x – 4)2 + 2y = 9 is :
(a) (2, 8)
(b) (7, 2)
(c) (4,9/2)
(d) (−4,−9/2)
Answer
C
Question. For what value of k, does the equation 9x2 + y2 = k (x2 – y2 – 2x) represent equation of a circle ?
(a) 1
(b) 2
(c) –1
(d) 4
Answer
D
Question. If the eccentricity of the hyperbola x2 – y2 sec2Θ = 4 is √3 times the eccentricity of the ellipse x2sec2Θ + y2 = 16, then the value of Θ equals
(a) π/6
(b) 3π/4
(c) π/3
(d) π/2
Answer
B
Question. The focal distance of a point on the parabola y2 = 8x is 4. Its ordinates are:
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 4
Answer
D
Question. If the equation of a circle is (4a − 3)x2 + ay2 + 6x − 2y + 2 = 0 , then its centre is
(a) (3, −1)
(b) (3, 1)
(c) (–3, 1)
(d) None of these
Answer
C
Question. A conic section with eccentricity e is a parabola if:
(a) e = 0
(b) e < 1
(c) e > 1
(d) e = 1
Answer
D
Question. An arch is in the form of semi-ellipse. It is 8 m wide and 2 m high at the centre. Then, the height of the arch at a point 1.5 m from one end is
(a) 1.56 m
(b) 2.4375 m
(c) 2.056 m
(d) 1.086 m
Answer
A
Question. Two common tangents to the circle x2 + y2 = 2a2and parabola y2 = 8ax are
(a) x = ±(y + 2a)
(b) y = ±(x + 2a)
(c) x = ±(y + a)
(d) y = ±(x + a)
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 4 2 3 1
(b) 1 2 3 4
(c) 1 3 2 4
(d) 4 3 2 1
Answer
D
Question. The latus rectum of parabola y2 = 5x + 4y + 1 is:
(a) 10
(b) 5
(c) 5/4
(d) 5/2
Answer
B
Question. If one of the diameters of the circle x2 + y2 – 2x – 6y + 6 = 0 is a chord to the circle with centre (2, 1), then the radius of the circle is
(a) √3
(b) √2
(c) 3
(d) 2
Answer
C
Question. The equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13, is
(a) 25x2 – 144y2 = 900
(b) 144x2 – 25y2 = 900
(c) 144x2 + 25y2 = 900
(b) 25x2 + 144y2 = 900
Answer
A
Question. The focal distance of a point on the parabola y2 = 12x is 4. What is the abscissa of the point ?
(a) 1
(b) – 1
(c) 2√3
(d) – 2
Answer
A
Question. The focus of the curve y2+ 4x – 6y + 13 = 0 is
(a) (2, 3)
(b) (–2, 3)
(c) (2, –3)
(d) (–2, –3)
Answer
B
STATEMENT TYPE QUESTIONS
Question. I. Equation of conjugate hyperbola is x2/a2 + y2/b2 = –1
II. Length of latus rectum of the conjugate hyperbola is 2a2/b.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. If the equation of the hyperbola is 9y2 – 4x2 = 36, then
I. the coordinates of foci are (0, ± √13)
II. the eccentricity is 2/√13.
III. the length of the latus rectum is 8.
(a) Only I is true.
(b) Only II is true.
(c) Only III is true.
(d) None of them is true.
Answer
A
Question. If the equation of the circle is x2 + y2 – 8x + 10y – 12 = 0, then
I. Centre of the circle is (4, –5).
II. Radius of the circle is √53 .
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. If the equation of the hyperbola is y2/9 − x2/27 = 1 , then
I. the coordinates of the foci are (0, ± 6)
II. the length of the latus rectum is 18 units.
III. the eccentricity is 4/5 .
(a) Only I is true.
(b) Only II is true.
(c) Only I and II is true.
(d) Only II and III is true.
Answer
C
Question. Consider the following statements.
I. The equation of a circle with centre (h, k) and the radius r is (x – h)2 + (y – k)2 = r2.
II. The equation of the parabola with focus at (a, 0), a > 0 and directrix x = –a is y2 = – 4ax
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Botha re false.
Answer
A

